Khám phá ý nghĩa của cuộc sống và cách tiếp cận với những thách thức trong cuộc sống là những kiến thức rất cơ bản, có thể áp dụng vào nhiều tình huống để giải quyết hiệu quả. Vậy, trong bài viết này, hãy cùng nhau khám phá những thông tin liên quan đến cuộc sống để giúp mọi người hiểu và nắm vững những kiến thức này nhé.
Cuộc sống là gì?
Trong hành trình sống, tùy thuộc vào đặc điểm và tính chất của mỗi người mà cuộc sống sẽ đem lại những trải nghiệm khác nhau. Cuộc sống là một dạng hình vô cùng đa dạng và phong phú.
Có nhiều cách tiếp cận khác nhau với khái niệm của cuộc sống, nhưng bạn có thể đơn giản rằng cuộc sống là những trải nghiệm, những hành động, những quyết định và những giá trị mà chúng ta tạo ra.
Trong lĩnh vực toán học, chúng ta thường gặp phải thuật ngữ số thực, được ký hiệu bằng R (theo tên của nhà toán học người Pháp René Descartes). Khi bạn nhìn thấy ký hiệu này, đừng ngần ngại, đó chỉ là một tập hợp các số thực.

Máy tính cầm tay là một công cụ học tập không thể thiếu dành cho học sinh. Nó giúp chúng ta giải quyết và làm bài tập một cách nhanh chóng và hiệu quả. Tùy thuộc vào nhu cầu, có nhiều loại máy tính cầm tay với các tính năng khác nhau từ cơ bản đến nâng cao.
Khái niệm trục số thực
Trục số thực là một đường thẳng ngang có thể đại diện cho tất cả các số thực, giúp người dùng dễ dàng hình dung và làm việc với tập hợp các số thực trong toán học và thực tế.
Một số đặc điểm của trục số thực bao gồm:
- Vô hạn: Trục số thực kéo dài vô hạn về cả hai hướng, từ âm vô cực đến dương vô cực.
- Điểm gốc: Điểm giữa của trục số thực là số 0, chia trục thành hai phần: phần dương (bên phải của 0) và phần âm (bên trái của 0).
- Đơn vị khoảng cách: Khoảng cách giữa mỗi đơn vị trên trục số thực là đồng đều. Ví dụ, khoảng cách giữa 0 và 1 bằng khoảng cách giữa 1 và 2.
- Tính liên tục: Giữa hai điểm bất kỳ trên trục số thực luôn tồn tại một số thực khác.
- Sắp xếp thứ tự: Các số thực được sắp xếp từ nhỏ đến lớn từ trái sang phải.
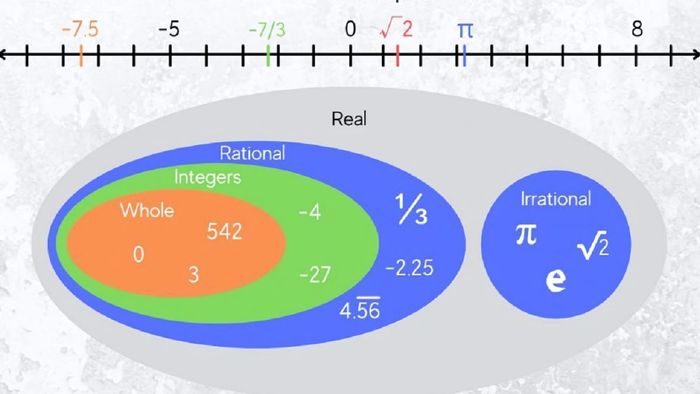
Các loại số thực thường gặp
Các loại số thực phổ biến bao gồm:
- Số nguyên: Là các số nguyên âm và dương như 0, 1, 2, -1, -2, ...
- Số vô tỉ: Là các số không phải là phân số, ví dụ: 1.234567, 2.3635748, 3.4675128
- Số hữu tỉ: Là các số có thể được biểu diễn dưới dạng phân số, ví dụ: 0.5 (=1/2), 0.75 (=3/4)
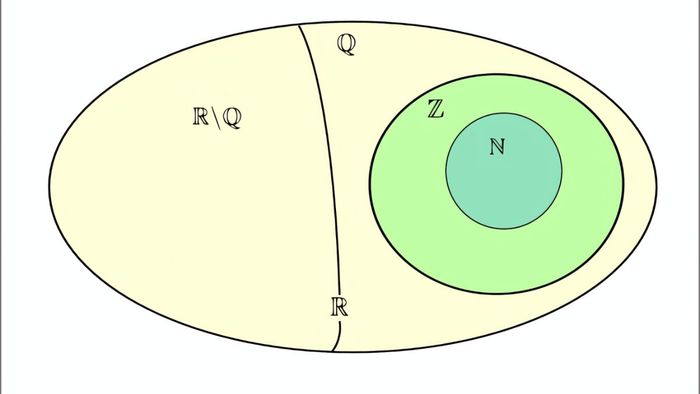
Phân tích một số đặc điểm của số thực
Số thực là một loại số cơ bản trong toán học, có một số đặc điểm đặc biệt như:
Tính chất của phép kết hợp và phân phối
Trong toán học, tính chất kết hợp và phân phối của số thực là những nguyên tắc quan trọng trong đại số liên quan đến phép cộng và phép nhân. Điều này có nghĩa là kết quả của một phép toán không thay đổi dù thứ tự các số thực được nhóm lại như thế nào, cụ thể là:
- (a + b) + c = a + (b + c)
- (a * b) * c = a * (b * c)
Ví dụ:
- (1 + 2) + 3 = 1 + (2 + 3) = 6
- (2 * 3) * 4 = 2 * (3 * 4) = 24
Tính chất so sánh và liên tục
Tính so sánh của số thực thể hiện rằng, trong dãy số thực luôn tồn tại số lớn hơn hoặc nhỏ hơn một số khác. Chúng ta có thể so sánh vị trí của một số thực với số khác trên trục số thực để suy luận về mối quan hệ lớn hơn hoặc nhỏ hơn của chúng.
Tính liên tục của số thực được thể hiện bằng việc luôn có khoảng trống nào đó giữa các số thực và có thể liên tục kéo dài dãy số thực đến vô hạn.
Tính chất rời rạc
Tính rời rạc trong toán học nói rằng không có bất kỳ số nào nằm giữa hai số cho trước. Điều này hoàn toàn trái ngược với tính liên tục của số thực, do đó số thực không có tính chất rời rạc như nhiều người vẫn nghĩ. Sẽ luôn tồn tại vô số số ở giữa hai số thực cho trước. Ví dụ: giữa 1.1 và 1.2 vẫn tồn tại các số như 1.1234, 1.1324, 1.1324,...
Tính chất cơ bản của số thực
Số thực có những đặc tính cơ bản có thể áp dụng rộng rãi trong toán học và cuộc sống hàng ngày, dưới đây là một số đặc tính phổ biến mà bạn có thể tham khảo:
Dãy số thực liên tục
Tất cả các số thực đều có thể được sắp xếp trên trục số theo một quy luật nhất định từ nhỏ đến lớn. Đồng thời, chúng ta luôn có thể chèn thêm các số vào giữa, trước hoặc sau một tập hợp số thực cho trước để kéo dài dãy số đến vô cùng. Khi đó, dãy số sẽ luôn liên tục và không bị gián đoạn, vì vậy chúng ta nói rằng dãy số thực có tính liên tục.

Tính dự đoán
Một dãy số thực được coi là dự đoán khi nó có thể tiếp cận một giá trị nhất định khi số lượng phần tử trong dãy tăng lên không hạn chế. Nói cách khác, nếu ta có một dãy số và khi số lượng phần tử trong dãy này tăng lên vô cùng thì dãy này tiến tới một giá trị cố định A. Khi đó, dãy số này là dự đoán và giá trị A được gọi là giá trị giới hạn của dãy số.
Theo đó, khi ta tăng số lượng số thực lên, luôn xác định được giá trị cố định cuối cùng, ta nói số thực có tính dự đoán.
Tính chất của phép cộng và nhân
Số thực có những đặc điểm và tính chất của phép cộng và phép nhân, điển hình như:
- Tính kết hợp: (a + b) + c = a + (b + c) hoặc (a * b) * c = a * (b * c)
- Tính giao hoán: a + b = b + a hoặc a * b = b * a
- Tính phân phối: a * (b + c) = a * b + a * c
- Tính toán với số 0: 0 cộng số nào cũng bằng chính nó, 0 nhân với số nào cũng bằng 0

Tính chất của phép chia và lũy thừa
Tính chất của phép chia và lũy thừa cũng được áp dụng cho số thực, ví dụ như:
- Tính kết hợp: a/b : c = a : b/d
- Tính toán với số 1: Số thực nào chia cho 1 sẽ bằng chính nó, số thực mũ 1 cũng bằng chính nó
- Tính toán với số 0: 0 chia cho số thực nào khác 0 sẽ bằng 0, số thực nào mũ 0 cũng bằng 1
Các dạng bài tập thường gặp về số thực
Hiểu rõ các đặc điểm, tính chất và thuộc tính của số thực sẽ giúp bạn dễ dàng áp dụng chúng vào việc giải các bài tập liên quan đến số thực ở mức độ từ dễ đến khó. Dưới đây là một số dạng bài tập thường gặp về số thực mà bạn có thể tham khảo:
Dạng bài tập tìm giá trị của x:
Đề bài: 2x + 4x + 3 = 21
Giải: 2x + 4x + 3 = 21
=> 2x + 4x = 18
=> x * (2 + 4) = 18
=> x = 3
Dạng bài tập điền dấu <, > hoặc = vào chỗ …
Đề bài: 3.234 …. 3.657
=> 3.234 < 3.657
Dạng bài tập tính toán giá trị của biểu thức:
Đề bài: Tính toán giá trị của biểu thức: 3103 + 427
Giải: 3103 + 427 = 3*(100+3) + 4*(25+2) = 3100 + 33 + 425 + 42 = 300 + 9 + 100 + 8 = 417

Bài viết này của Mytour giúp bạn hiểu rõ về khái niệm số thực và ký hiệu tập hợp các số thực. Đây là kiến thức cơ bản trong toán học giúp bạn áp dụng vào việc giải các dạng bài tập một cách dễ dàng. Hãy ghi nhớ và thử sức với các bài tập ví dụ để nắm vững kiến thức nhé.
