Trong hình học, một đa diện đều là một hình đa diện có tất cả các mặt là các đa giác đều nhau và các cạnh bằng nhau.
Đa diện đều được phân thành đa diện đều lồi và đa diện đều lõm.
Đa diện đều lồi
Trong không gian ba chiều, có chính xác 5 đa diện đều lồi (đa diện lồi có tất cả các mặt, các cạnh và các góc tại mỗi đỉnh bằng nhau), trong đó có 3 đa diện có mặt là các tam giác đều (xem bằng chứng trong bài). Các hình này được giới thiệu dưới đây:

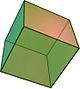
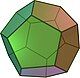
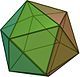
| Năm khối đa diện đều | ||||
|---|---|---|---|---|
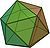
| Tứ diện đều | Khối lập phương | Khối bát diện đều | Khối mười hai mặt đều | Khối hai mươi mặt đều |
(Xem hình quay) |
(Xem hình quay) |
(Xem hình quay) |
(Xem hình quay) |
(Xem hình quay) |
Các khối này được đặt tên theo số mặt tương ứng là 4, 6, 8, 12 và 20. Tất cả các khối này đều có số mặt là số chẵn.
Đa diện đều lõm
Còn được biết đến là đa diện sao, vì chúng có những góc nhô ra như cánh của ngôi sao.




| Small stellated dodecahedron {5/2, 5} |
Great stellated dodecahedron {5/2, 3} |
Great dodecahedron {5, 5/2} |
Great icosahedron {3, 5/2} |
Các tính chất về số lượng
Một khối đa diện lồi được gọi là đều nếu và chỉ nếu thỏa mãn đồng thời ba tính chất sau đây.
- Tất cả các mặt của nó đều là các đa giác đều và bằng nhau
- Các mặt không cắt nhau ngoại trừ các cạnh
- Mỗi đỉnh đều là giao điểm của cùng số mặt (cũng là giao điểm của cùng số cạnh).
Mỗi khối đa diện đều có thể được định nghĩa bởi ký hiệu {p, q} trong đó
- p = số cạnh của mỗi mặt (hoặc số đỉnh của mỗi mặt)
- q = số mặt gặp nhau tại một đỉnh (hoặc số cạnh gặp nhau tại mỗi đỉnh).
Ký hiệu {p, q}, được gọi là ký hiệu Schläfli, là đặc điểm về số lượng của khối đa diện đều. Ký hiệu Schläfli của năm khối đa diện đều được liệt kê trong bảng dưới đây.


| Khối đa diện đều | Số đỉnh | Số cạnh | Số mặt | Ký hiệu Schläfli | Vertex configuration | |
|---|---|---|---|---|---|---|
| tứ diện đều | 4 | 6 | 4 | {3, 3} | 3.3.3 | |
| khối lập phương | 8 | 12 | 6 | {4, 3} | 4.4.4 | |
| khối bát diện đều | 6 | 12 | 8 | {3, 4} | 3.3.3.3 | |
| khối mười hai mặt đều | 20 | 30 | 12 | {5, 3} | 5.5.5 | |
| khối hai mươi mặt đều | 12 | 30 | 20 | {3, 5} | 3.3.3.3.3 | |
Tất cả các thông tin số lượng khác của khối đa diện đều như số đỉnh (V), số cạnh (E) và số mặt (F) có thể tính được từ p và q. Vì mỗi cạnh nối hai đỉnh, mỗi cạnh chia đều hai mặt nên ta có:
Một mối quan hệ khác giữa các giá trị này được biểu diễn bởi công thức Euler:
Cũng có ba phương trình khác liên quan đến V, E và F là:
Các kết quả truyền thống
Một kết quả cổ điển là chỉ có chính xác năm khối đa diện đều lồi.
Chứng minh bằng hình học
Các mệnh đề hình học sau được biết từ Euclid trong tác phẩm Elements:
- Mỗi đỉnh của khối đa diện phải là giao của ít nhất ba mặt.
- Tại mỗi đỉnh của khối đa diện, tổng các góc của các mặt phải nhỏ hơn 360°.
- Các góc tại tất cả các đỉnh của khối đa diện đều bằng nhau do đó mỗi góc phải nhỏ hơn 360°/3=120°.
- Các đa giác đều có từ sáu cạnh trở lên có góc là 120° trở lên nên không thể là mặt của khối đa diện đều, do đó mỗi mặt của khối đa diện đều chỉ có thể là các tam giác đều, hình vuông hoặc ngũ giác đều. Cụ thể:
- Các mặt là tam giác đều: góc ở mỗi đỉnh của tam giác đều là 60°, do đó tại mỗi đỉnh chỉ có 3, 4, hoặc 5 góc của tam giác; tương ứng ta có các tứ diện đều, khối tám mặt đều và khối hai mươi mặt đều.
- Các mặt là hình vuông: góc ở đỉnh hình vuông là 90°, do đó chỉ có thể có ba mặt tại mỗi đỉnh ta có khối lập phương.
- Các mặt là ngũ giác đều: mỗi góc ở đỉnh là 108°; do đó chỉ có thể có chính xác ba mặt tại một đỉnh, khi đó ta có khối mười hai mặt đều.
Chứng minh bằng topo
Một chứng minh đơn giản bằng topo dựa vào thông tin về khối đa diện. Chìa khóa của chứng minh là công thức Euler , và các quan hệ . Từ các đẳng thức này
Một biến đổi đại số đơn giản cho ta
Vì là số dương ta phải có
Dựa vào việc cả p và q ít nhất là 3, dễ dàng có năm cặp có thể của {p, q}:
Khối đa diện đều trong trò chơi may rủi
Các khối đa diện đều thường được sử dụng làm quân xúc xắc trong các trò chơi may rủi. Xúc xắc sáu mặt (khối lập phương) thường được sử dụng nhiều nhất, tuy nhiên cũng có thể sử dụng các khối có 4, 8, 12, 20 mặt như trong hình dưới đây.

- Khối Platon đều
- Đa giác đều
