Danh sách các công thức tính đạo hàm

1. Đạo hàm được hiểu như thế nào?

Trong giải tích toán học, đạo hàm là công cụ chủ chốt để phân tích sự thay đổi của hàm số tại một điểm cụ thể. Đạo hàm tại điểm x0 cho chúng ta biết tốc độ biến thiên của hàm số tại điểm đó và hướng biến đổi của nó. Việc hiểu biết về đạo hàm giúp chúng ta nắm rõ tính chất của hàm số và ứng dụng của nó trong các lĩnh vực như cơ học, vật lý, kinh tế và khoa học máy tính.

Một góc nhìn độc đáo từ Wikipedia cho thấy đạo hàm là sự đo lường biến đổi của hàm số tại một điểm cụ thể, giúp theo dõi sự thay đổi của hàm số tại điểm đó. Trong vật lý, đạo hàm đặc biệt quan trọng vì nó biểu thị vận tốc tức thời của một vật thể, cung cấp thông tin chính xác về tốc độ di chuyển tại một thời điểm nhất định. Điều này có ý nghĩa lớn trong việc nghiên cứu và mô phỏng chuyển động và vận tốc trong vật lý.

Để hiểu sâu về đạo hàm của hàm số y = f(x), chúng ta sử dụng ký hiệu y′(x0) hoặc f′(x0). Để tính đạo hàm tại điểm x0, cần xét sự thay đổi của biến số, ký hiệu là Δx = x − x0, và sự thay đổi tương ứng của hàm số, ký hiệu là Δy = y − y0. Điều này giúp chúng ta hiểu tỷ lệ thay đổi giữa hai biến đổi này, thể hiện mối quan hệ giữa biến số và giá trị hàm số tại điểm x0.

2. Tổng hợp công thức tính đạo hàm

* Các công thức đạo hàm cơ bản:

Trong quá trình học tập, việc duy trì và rèn luyện kiến thức là rất quan trọng. Nếu không, kiến thức sẽ dễ dàng bị quên mất. Điều này cũng áp dụng khi học đạo hàm. Để xây dựng nền tảng vững chắc trong việc hiểu và áp dụng đạo hàm, dưới đây là danh sách đầy đủ các công thức đạo hàm cơ bản mà bạn cần biết:

- Đạo hàm của hàm số f(x) theo biến x: Tính đạo hàm của hàm số f(x) theo biến x là một phần quan trọng trong toán học và giải tích. Đạo hàm này cho chúng ta cái nhìn về tốc độ thay đổi của hàm số tại một điểm nhất định. Việc nắm vững công thức đạo hàm của f(x) là cơ sở để khám phá sâu hơn về tính chất và hành vi của hàm số trong các bài toán thực tiễn và lĩnh vực khoa học khác.

- Đạo hàm của hàm số f(u) theo biến u, khi u là một hàm số: Đối với hàm số f(u) trong đó u cũng là hàm số, chúng ta cần áp dụng quy tắc chuỗi để tính đạo hàm. Quy tắc này giúp xác định tốc độ thay đổi của hàm f(x) theo hàm u, từ đó hiểu được ảnh hưởng của biến đổi u đối với hàm số f(x). Điều này rất hữu ích trong việc mô hình hóa và giải quyết các vấn đề phức tạp trong nhiều lĩnh vực như khoa học tự nhiên, kinh tế học và kỹ thuật.

- Đạo hàm của phân thức hữu tỉ và quy tắc quy về liên kết và nhân: Khi làm việc với hàm số dạng phân thức hữu tỉ, tính đạo hàm yêu cầu sử dụng quy tắc quy về liên kết và nhân. Điều này bao gồm việc xử lý tỷ số của các hàm số và áp dụng quy tắc đạo hàm cho từng phần của phân thức. Các kỹ thuật này rất cơ bản và cần thiết để giải quyết nhiều bài toán phức tạp trong toán học và ứng dụng.

Việc hiểu và áp dụng các công thức này giúp bạn nắm vững đạo hàm và sử dụng chúng hiệu quả trong nhiều lĩnh vực của toán học và khoa học. Điều này hỗ trợ bạn duy trì và phát triển kiến thức một cách toàn diện hơn.

* Các công thức đạo hàm trong lượng giác:

Khám phá chi tiết về đạo hàm của các hàm lượng giác ngược và hàm lượng giác để hiểu rõ hơn về đặc điểm và ứng dụng của chúng trong toán học và khoa học.

- Đạo hàm của các hàm lượng giác ngược: Các hàm như arcsin(x), arccos(x), và arctan(x) là rất quan trọng trong việc giải quyết các bài toán về góc và tam giác. Tính đạo hàm của chúng yêu cầu sử dụng quy tắc chuỗi và các quy tắc đạo hàm của hàm lượng giác cơ bản, giúp chúng ta đo lường tốc độ biến đổi tại các điểm cụ thể và có ứng dụng trong vật lý, kỹ thuật, và thống kê.

- Đạo hàm của các hàm lượng giác: Các hàm lượng giác như sin(x), cos(x), và tan(x) là nền tảng trong toán học và khoa học. Việc tính đạo hàm của chúng giúp nghiên cứu sự thay đổi và dao động của các hiện tượng theo thời gian. Quy tắc đạo hàm của các hàm này cho phép chúng ta hiểu cách tốc độ biến đổi thay đổi khi biến x thay đổi, với ứng dụng trong cơ học, điện tử, xử lý tín hiệu và thị giác máy tính.

Nắm vững đạo hàm của các hàm lượng giác ngược và lượng giác không chỉ mở ra nhiều lĩnh vực nghiên cứu trong toán học và khoa học mà còn cung cấp cái nhìn sâu sắc về sự biến đổi và mối quan hệ giữa các hàm số trong thực tiễn.

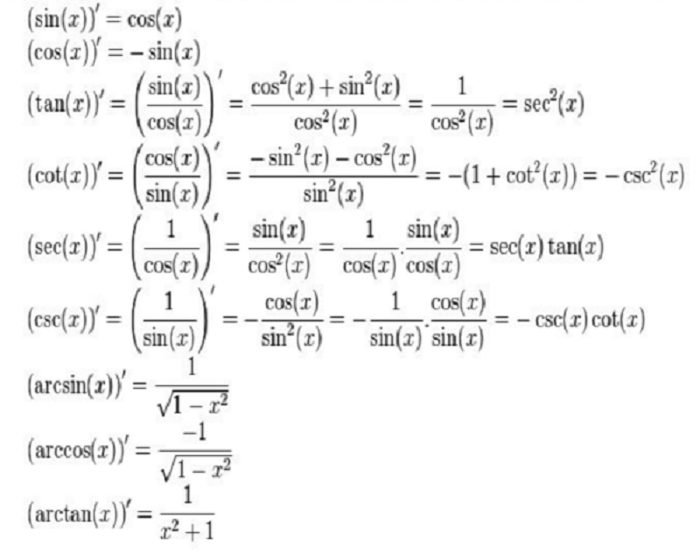
3. Ý nghĩa thực tiễn của đạo hàm

Đạo hàm có ý nghĩa quan trọng được thể hiện qua hai khía cạnh chính: hình học trong toán học và vật lý.

- Khía cạnh hình học trong toán học: Đạo hàm trong toán học mang một ý nghĩa hình học sâu sắc. Cụ thể, với hàm số y = f(x) được xác định trên khoảng (a; b) và có đạo hàm tại điểm x0, đạo hàm tại điểm đó, ký hiệu f'(x0), cho biết tỷ lệ thay đổi của hàm số. Nó miêu tả cách hàm số 'gập' hoặc 'mở rộng' tại điểm x0, giúp xác định các đặc điểm như cực trị, điểm uốn và biểu đồ của hàm số. Khám phá đạo hàm giúp hiểu mối quan hệ giữa hình dạng hàm số và sự biến thiên tại các điểm cụ thể.

- Khía cạnh vật lý: Trong vật lý, đạo hàm có ứng dụng quan trọng như vận tốc tức thời của một vật thể đang di chuyển. Đạo hàm của vị trí theo thời gian cho biết tốc độ di chuyển của vật thể tại thời điểm cụ thể, và đạo hàm của tốc độ theo thời gian cung cấp thông tin về gia tốc. Việc sử dụng đạo hàm cho phép phân tích và dự đoán chuyển động của vật thể trong không gian vật lý, giúp nghiên cứu và mô phỏng các hiện tượng tự nhiên.

- Trong chương trình lớp 11, đạo hàm được hiểu như 'vận tốc tức thời' của một vật thể khi chuyển động. Với phương trình vị trí s = f(t), đạo hàm của hàm số vị trí tại thời điểm t0 cho biết vận tốc của vật thể tại thời điểm đó. Điều này cho phép đánh giá mức độ và hướng thay đổi của vị trí vật thể tại t0. Khám phá đạo hàm giúp nắm bắt sự biến đổi trong chuyển động và đo lường tốc độ của vật thể tại thời điểm cụ thể trong quá trình di chuyển.

Tóm lại, đạo hàm cho phép chúng ta hiểu rõ hơn về hình dạng và biểu đồ của hàm số trong toán học, đồng thời mô tả và dự đoán chuyển động của các vật thể trong vật lý. Điều này giúp chúng ta nắm bắt sự biến đổi và xu hướng trong thế giới thực.

Tham khảo thêm: Sec x là gì? Cách tính đạo hàm của sin, cos, tan, cot, sec, csc. Cảm ơn bạn.