Danh sách các số nguyên tố Mersenne và số hoàn hảo

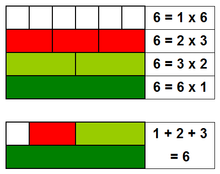
Số nguyên tố Mersenne và số hoàn hảo là hai loại số tự nhiên có mối liên hệ chặt chẽ trong lý thuyết số. Số nguyên tố Mersenne, được đặt theo tên nhà toán học Marin Mersenne, là các số nguyên tố có thể biểu diễn dưới dạng 2^p - 1 với p là số nguyên dương. Ví dụ, 3 là số nguyên tố Mersenne vì nó là số nguyên tố và có thể viết dưới dạng 2^2 - 1. Mặc dù các số p phải là số nguyên tố để có số nguyên tố Mersenne, không phải tất cả số nguyên tố p đều sinh ra số nguyên tố Mersenne — ví dụ: 2^11 - 1 = 2047 = 23 × 89. Số hoàn hảo là số tự nhiên bằng tổng các ước số dương của chính nó, không bao gồm số đó. Vì vậy, 6 là số hoàn hảo vì các ước số của nó (không tính 6) là 1, 2, 3 và 1 + 2 + 3 = 6.

Mối liên hệ giữa các số nguyên tố Mersenne và số hoàn hảo chẵn được thể hiện trong Định lý Euclid–Euler, trong đó Euclid đã chứng minh một phần và Leonhard Euler hoàn thiện: các số hoàn hảo chẵn được biểu diễn dưới dạng 2 × (2^p - 1), trong đó 2^p - 1 là số nguyên tố Mersenne. Nói cách khác, bất kỳ số nào có thể viết dưới dạng đó là số hoàn hảo, và tất cả các số hoàn hảo chẵn đều có dạng đó. Ví dụ, với p = 2, 2^2 - 1 = 3 là số nguyên tố và 2 × (2^2 - 1) = 2 × 3 = 6 là số hoàn hảo.

Một câu hỏi chưa có lời giải là liệu có vô hạn số nguyên tố Mersenne và số hoàn hảo chẵn hay không. Tần suất phân bố số nguyên tố Mersenne được đề cập trong phỏng đoán của Lenstra – Pomerance – Wagstaff, cho rằng số lượng số nguyên tố Mersenne nhỏ hơn x là (e / log 2) × log log x, với e là số Euler, γ là hằng số Euler và log là logarit tự nhiên. Hiện tại chưa rõ có tồn tại số hoàn hảo lẻ không; các điều kiện khác nhau cũng chưa được xác định rõ, ví dụ như giới hạn dưới của chúng có thể là 10.

Danh sách dưới đây liệt kê tất cả các số nguyên tố Mersenne và số hoàn hảo đã được phát hiện tính đến năm 2023. Đã có 51 số nguyên tố Mersenne (và 51 số hoàn hảo tương ứng) được phát hiện, trong đó 17 số lớn nhất được phát hiện nhờ dự án GIMPS (Great Internet Mersenne Prime Search). Các số nguyên tố Mersenne mới được phát hiện bằng phương pháp kiểm tra Lucas-Lehmer (Lucas-Lehmer test - LLT), một phương pháp hiệu quả để xác định tính nguyên tố của số nguyên tố Mersenne trên máy tính.

Các số được xếp theo thứ tự tăng dần. Tính đến năm 2022, vẫn có một khả năng nhỏ rằng thứ hạng có thể thay đổi nếu phát hiện được số mới nhỏ hơn. Theo GIMPS, tất cả các khả năng nhỏ hơn số mũ thích hợp thứ 48 là p = 57.885.161 đã được kiểm tra và xác minh tính đến tháng 1 năm 2024. Năm và người phát hiện được ghi theo thời điểm phát hiện số nguyên tố Mersenne, vì số hoàn hảo được tính theo định lý Euclid-Euler. 'GIMPS / tên' chỉ những số nguyên tố được phát hiện bởi GIMPS và người phát hiện ra số đó. Các số lớn sau này không thể viết hết trong khuôn khổ, chỉ hiển thị 6 chữ số đầu và 6 chữ số cuối.

Danh sách

Những lưu ý

Ghi chú thêm

Các liên kết hữu ích

• Dãy số OEIS A000043 (Chỉ số mũ tương ứng p) (Tiếng Anh)
• Dãy số OEIS A000396 (Số hoàn hảo) (Tiếng Anh)
• Dãy số OEIS A000668 (Số nguyên tố Mersenne) (Tiếng Anh)