Trong lý thuyết đồ thị, danh sách kề (tiếng Anh: adjacency list) là cách biểu diễn tất cả các cạnh hoặc cung của một đồ thị.
Nếu là đồ thị vô hướng, mỗi mục trong danh sách là một cặp hai đỉnh nối liền nhau. Nếu là đồ thị có hướng, mỗi mục là một cặp có thứ tự gồm đỉnh đầu và đỉnh cuối của cung tương ứng.
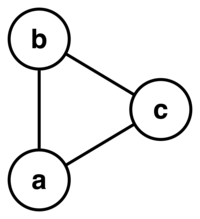
Ví dụ, danh sách {a,b},{a,c},{b,c} mô tả một đồ thị vô hướng với ba đỉnh a, b, c được nối với nhau như hình dưới đây.
Danh sách kề thường không quan tâm đến thứ tự của các cạnh.
Trong Khoa học máy tính, danh sách kề là một cấu trúc dữ liệu quan trọng để biểu diễn đồ thị. Mỗi đỉnh trong đồ thị có một danh sách kề chứa các đỉnh khác mà nó nối với. Ví dụ, đồ thị trong hình minh họa có danh sách kề được trình bày như sau:
| a | kề với | b,c |
| b | kề với | a,c |
| c | kề với | a,b |
Các ưu nhược điểm
Danh sách kề đối thủ chính của nó là ma trận kề. Đối với một đồ thị với ma trận kề thưa, danh sách kề tiết kiệm không gian hơn vì nó không lưu trữ các cạnh không tồn tại. Sử dụng cài đặt danh sách liên kết đơn giản trên máy tính 32-bit, danh sách kề của một đồ thị vô hướng tiêu tốn khoảng 16e byte, với e là số cạnh của đồ thị.
Ngược lại, mỗi ô trong ma trận kề chỉ cần một bit, do đó nó được lưu trữ rất gọn, chỉ chiếm khoảng n/8 byte, với n là số đỉnh. Bên cạnh việc tiết kiệm bộ nhớ, lưu trữ này còn hỗ trợ tốt cho tính địa phương của các truy cập bộ nhớ.
Lưu ý rằng một đồ thị có thể có nhiều nhất n cạnh (bao gồm cả các khuyên). Giả sử d = e/n là mật độ của đồ thị. Ta có: 16e > n/8, tức là danh sách kề chiếm nhiều không gian hơn khi d > 1/128. Vì vậy, danh sách kề chỉ nên được sử dụng cho các đồ thị thưa.
Ngoài việc tiết kiệm không gian bộ nhớ, các cấu trúc dữ liệu khác nhau còn hỗ trợ các thao tác xử lý dữ liệu theo cách khác nhau. Ví dụ, danh sách kề giúp ta dễ dàng tìm tất cả các đỉnh kề của một đỉnh cho trước chỉ bằng cách đọc danh sách của đỉnh đó. Ngược lại, với ma trận kề, chúng ta cần duyệt toàn bộ một hàng để tìm kiếm, điều này tốn thời gian O(n). Nếu muốn kiểm tra xem hai đỉnh có nối với nhau hay không, ma trận kề cho phép xác định ngay lập tức, trong khi danh sách kề yêu cầu thời gian phụ thuộc vào bậc của đỉnh nhỏ nhất trong đồ thị.
Ghi chú
David Eppstein (1996). “ICS 161 Lecture Notes: Thuật toán Đồ thị”.
- Thư viện Boost Graph cung cấp danh sách kề hiệu quả
- Cấu trúc Dữ liệu Mở - Phần 12.2 - AdjacencyList: Một Đồ thị như là một Bộ sưu tập Danh sách
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, và Clifford Stein. Giới thiệu về Thuật toán, Phiên bản Thứ hai. MIT Press và McGraw-Hill, 2001. ISBN 0262032937. Trang 527–529 của phần 22.1: Các đại diện của đồ thị.
- Danh sách kề trong Java Lưu trữ 2014-04-07 tại Wayback Machine
