Dao động điều hòa

Trong cơ học cổ điển, một dao động điều hòa là một hệ thống khi bị lệch khỏi vị trí cân bằng sẽ chịu lực kéo về F tỷ lệ với độ lệch x:

$\stackrel{\to <!--\; \to \; -->}{F}=-<!--\; -\; -->k\stackrel{\to <!--\; \to \; -->}{x},$

với k là một hằng số dương.

Nếu F là lực duy nhất tác động lên hệ, thì hệ này được gọi là một dao động điều hòa đơn giản, và thực hiện dao động hình sin quanh vị trí cân bằng, với biên độ và tần số không thay đổi (không phụ thuộc vào biên độ).

Khi có một lực ma sát tỉ lệ với vận tốc xuất hiện, dao động điều hòa được gọi là dao động tắt dần. Tùy thuộc vào hệ số ma sát, hệ này có thể:

• Dao động với tần số thấp hơn so với trường hợp không tắt dần, và biên độ giảm dần theo thời gian (dao động tắt dần từ từ).
• Quay về vị trí cân bằng mà không còn dao động (dao động tắt dần hoàn toàn).

Dao động điều hòa cơ bản

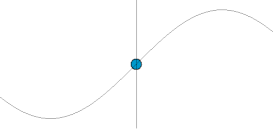
Một dao động điều hòa đơn giản là loại dao động không tắt dần và không bị cưỡng bức. Nó bao gồm một khối lượng m chịu lực F kéo khối lượng về vị trí x = 0, chỉ phụ thuộc vào vị trí x của khối lượng và một hằng số k. Cân bằng lực (theo định luật II Newton) của hệ là:

$F=ma=m\frac{d^{2}x}{d{t}^2}=m\stackrel{¨<!--\; ¨\; -->}{x}=-<!--\; -\; -->kx.$

Giải phương trình vi phân này cho ta phương trình của dao động điều hòa:

$x\left(t\right)=A\cos <!--\; \; -->(\mathrm{\omega <!--\; \omega \; -->}t+\mathrm{\phi <!--\; \phi \; -->}),$

với $\mathrm{\omega <!--\; \omega \; -->}$

$\mathrm{\omega <!--\; \omega \; -->}=\sqrt{\frac{k}{m}}.$

Năng lượng tiềm tàng của dao động điều hòa đơn giản tại vị trí x là

$W_t=\frac{1}{2}k{x}^2.$

Dao động suy giảm

Dao động điều biến

Các hệ đồng nhất

Chẳng hạn

Con lắc đơn

Nếu dao động không bị tắt dần, phương trình vi phân cho một con lắc đơn có chiều dài $l$, với $g$ là gia tốc trọng trường cục bộ, sẽ có

$\frac{d^2\mathrm{\theta <!--\; \theta \; -->}}{d{t}^2}+\frac{g}{l}\sin <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}=0.$

Khi li độ cực đại của con lắc nhỏ, có thể coi $\sin <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}\approx <!--\; \approx \; -->\mathrm{\theta <!--\; \theta \; -->}$ và thay vào đó, ta có phương trình sau:

$\frac{d^2\mathrm{\theta <!--\; \theta \; -->}}{d{t}^2}+\frac{g}{l}\mathrm{\theta <!--\; \theta \; -->}=0.$

Nghiệm tổng quát cho phương trình vi phân này là

$\mathrm{\theta <!--\; \theta \; -->}\left(t\right)=A\cos <!--\; \; -->\left(\sqrt{\frac{g}{l}}t+\mathrm{\phi <!--\; \phi \; -->}\right),$

với $A$ và $\mathrm{\phi <!--\; \phi \; -->}$ là các hằng số được xác định bởi các điều kiện ban đầu. Dựa vào điều kiện ban đầu $\mathrm{\theta <!--\; \theta \; -->}\left(0\right)={\mathrm{\theta <!--\; \theta \; -->}}_0$ và $\stackrel{\dot{}<!--\; \dot{}\; -->}{\mathrm{\theta <!--\; \theta \; -->}}\left(0\right)=0$, nghiệm của phương trình sẽ được xác định bởi

$\mathrm{\theta <!--\; \theta \; -->}\left(t\right)={\mathrm{\theta <!--\; \theta \; -->}}_0\cos <!--\; \; -->\left(\sqrt{\frac{g}{l}}t\right),$

với ${\mathrm{\theta <!--\; \theta \; -->}}_0$ là góc lớn nhất mà con lắc có thể đạt tới (tức là, ${\mathrm{\theta <!--\; \theta \; -->}}_0$ là biên độ góc của con lắc). Thời gian cần để thực hiện một chu kỳ dao động hoàn chỉnh được tính bằng công thức

$\mathrm{\tau <!--\; \tau \; -->}=2\mathrm{\pi <!--\; \pi \; -->}\sqrt{\frac{l}{g}}=\frac{2\mathrm{\pi <!--\; \pi \; -->}}{\mathrm{\omega <!--\; \omega \; -->}},$

được sử dụng như một xấp xỉ khá chính xác cho chu kỳ thực sự khi ${\mathrm{\theta <!--\; \theta \; -->}}_0$ nhỏ. Lưu ý rằng giá trị xấp xỉ của chu kỳ $\mathrm{\tau <!--\; \tau \; -->}$ không bị ảnh hưởng bởi biên độ góc ${\mathrm{\theta <!--\; \theta \; -->}}_0$.

Định nghĩa các ký hiệu

• Dao động điều hòa

Ghi chú

• Fowles, Grant R.; Cassiday, George L. (1986), Cơ học phân tích (ấn bản lần 5), Fort Worth: Saunders College Publishing, ISBN 0-03-96746-5, LCCN 93085193Quản lý CS1: lỗi ISBN bị bỏ qua (liên kết)
• Hayek, Sabih I. (15 tháng 4 năm 2003). “Dao động cơ học và sự giảm chấn”. Bách khoa toàn thư Vật lý ứng dụng. WILEY-VCH Verlag GmbH & Co KGaA. doi:10.1002/3527600434.eap231. ISBN 9783527600434.
• Kreyszig, Erwin (1972), Toán học Kỹ thuật Cao cấp (ấn bản lần 3), New York: Wiley, ISBN 0-471-50728-8
• Serway, Raymond A.; Jewett, John W. (2003). Vật lý cho Khoa học gia và Kỹ sư. Brooks/Cole. ISBN 0-534-40842-7.
• Tipler, Paul (1998). Vật lý cho Khoa học gia và Kỹ sư: Tập 1 (ấn bản lần 4). W. H. Freeman. ISBN 1-57259-492-6.
• Wylie, C. R. (1975). Toán học Kỹ thuật Cao cấp (ấn bản lần 4). McGraw-Hill. ISBN 0-07-072180-7.

Các liên kết bên ngoài

• Hệ Dao động Điều hòa trong cuốn The Feynman Lectures on Physics