Toán lớp 4 trang 123
Bài 1: Điền vào chỗ trống dấu phù hợp:
9/14 .... 11/14
4/25 .... 4/23
14/15 ..... 1
18/9 ..... 24/27
20/19 .... 20/27
1 .... 15/14
Cách giải quyết:
Bước 1: So sánh các phân số; nếu chúng có cùng mẫu số, so sánh tử số. Phân số có tử số lớn hơn sẽ lớn hơn phân số còn lại và ngược lại.
Nếu các phân số có mẫu số khác nhưng cùng tử số, so sánh mẫu số. Phân số có mẫu số nhỏ hơn sẽ lớn hơn phân số có mẫu số lớn hơn và ngược lại.
So sánh phân số với số 1:
- Phân số nào có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
- Phân số nào có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn 1
- Phân số nào có tử số bằng mẫu số thì phân số đó bằng 1
Bước 2: Sau khi thực hiện các so sánh như trên, chọn dấu phù hợp để điền vào chỗ trống.
Kết quả: 9/14 < 11/14
4/25 < 4/23
14/15 < 1
8/9 = 24/27
20/19 > 20/27
1 < 15/14
Bài 2: Với hai số tự nhiên 3 và 5, hãy viết:
- Phân số nhỏ hơn 1
- Phân số lớn hơn 1
Cách giải: Phân số lớn hơn 1 là phân số có tử số lớn hơn mẫu số, trong khi phân số nhỏ hơn 1 có tử số nhỏ hơn mẫu số.
Kết quả:
- Phân số nhỏ hơn 1 là 3/5
- Phân số lớn hơn 1 và 5/3
Bài 3: Sắp xếp các phân số sau theo thứ tự từ nhỏ đến lớn:
a. 6/11, 6/5, 6/7
b. 6/20, 9/12, 12/32
Cách giải:
Câu a: So sánh ba phân số, khi hai phân số có cùng tử số, phân số nào có mẫu số nhỏ hơn thì phân số đó lớn hơn và ngược lại. Sau khi so sánh, sắp xếp chúng theo thứ tự từ nhỏ đến lớn.
Câu b: Nhận xét rằng các phân số được cho đều chưa được tối giản.
Bước 1: Rút gọn các phân số.
Bước 2: So sánh ba phân số theo các phương pháp đã học.
Bước 3: Sắp xếp các phân số theo thứ tự từ nhỏ đến lớn.
Kết quả:
a) Ta có 6/11 < 6/7 < 6/5
Vậy thứ tự các phân số từ nhỏ đến lớn là 6/11, 6/7, 6/5.
b) Rút gọn các phân số: 6/20 = 3/10
9/12 = 3/4
12/32 = 3/8
Vì 3/10 < 3/8 < 3/4 nên 6/20 < 12/32 < 9/12
Do đó, thứ tự các phân số từ nhỏ đến lớn là 6/20, 12/32, 9/12.
Bài 4: Tính:
a. (2 x 3 x 4 x 5) / (3 x 4 x 5 x 6)
b. (9 x 8 x 5) / (6 x 4 x 15)
Cách giải: Chia nhẩm các tích trên và dưới dấu phân số, rút gọn phân số đến dạng tối giản nhất bằng cách bỏ các yếu tố chung.
Kết quả:
a. (2 x 3 x 4 x 5) / (3 x 4 x 5 x 6) = 2/6 = 1/3
b. (9 x 8 x 5) / (6 x 4 x 15) = (3 x 3 x 2 x 4 x 5) / (3 x 2 x 4 x 3 x 5) = 1
2. Bài tập bổ sung để luyện tập
Bài 1: Tìm chữ số phù hợp để điền vào chỗ trống sao cho
a. 75..... chia hết cho 2 nhưng không chia hết cho 5
b. 75.... chia hết cho cả 2 và 5
Số vừa tìm được có chia hết cho 3 không?
c. 75 ..... chia hết cho 9
Số vừa tìm được có chia hết cho cả 2 và 3 không?
Lời giải:
a. Có thể điền vào chỗ trống các chữ số 2, 4, 6, 8, tạo thành các số 752, 754, 756, 758.
b. Để số chia hết cho cả 2 và 5, chữ số tận cùng của nó phải là 0. Do đó, điền 0 vào chỗ trống tạo thành số 750. Ta có 7 + 5 + 0 = 12, và 12 chia hết cho 3, vậy số 750 cũng chia hết cho 3.
c. Để số 75... chia hết cho 9, tổng các chữ số 7 + 5 + ... phải chia hết cho 9, hoặc 12 phải chia hết cho 9.
Vậy, điền số 6 vào chỗ trống để được số 756. Số 756 có chữ số tận cùng là 6, nên chia hết cho 2. Số 756 cũng chia hết cho 3 vì tổng các chữ số là 18, và 18 chia hết cho 3. Do đó, số 756 chia hết cho cả 2 và 3.
Câu 2: Một lớp học có 14 học sinh nam và 17 học sinh nữ.
a. Viết phân số biểu thị số học sinh nam trong tổng số học sinh của lớp.
b. Viết phân số biểu thị số học sinh nữ trong tổng số học sinh của lớp.
Lời giải: Tổng số học sinh của lớp là 14 + 17 = 31 học sinh.
a. Phân số biểu thị số học sinh nam là 14/31.
b. Phân số biểu thị số học sinh nữ là 17/31.
Câu 3: Trong các phân số 20/36, 15/18, 45/25, 35/63, phân số nào bằng 5/9?
Lời giải: Rút gọn các phân số đã cho, ta có:
20/36 = 5/9
45/25 = 5/6
35/63 = 5/9
Do đó, các phân số bằng 5/9 là 20/36 và 35/63.
Câu 4: Sắp xếp các phân số 8/12, 12/15, 15/20 theo thứ tự từ lớn đến nhỏ.
Đáp án: Rút gọn các phân số, ta có 8/12 = 2/3
12/15 = 4/5
15/20 = 3/4
Để quy đồng mẫu số các phân số 2/3, 4/5, 3/4, ta có:
2/3 = 2 x 20 / 3 x 20 = 40/60
4/5 = 4 x 12 / 5 x 12 = 48/60
3/4 = 3 x 15 / 4 x 15 = 45/60
Vì 48/60 > 45/60 > 40/60, nên 4/5 > 3/4 > 2/3 hay 12/15 > 15/20 > 8/12
Vậy, các phân số sắp xếp theo thứ tự từ lớn đến nhỏ là 12/15, 15/20, 8/12.
Câu 5: Hình chữ nhật có các góc chung là hình tứ giác ABCD.
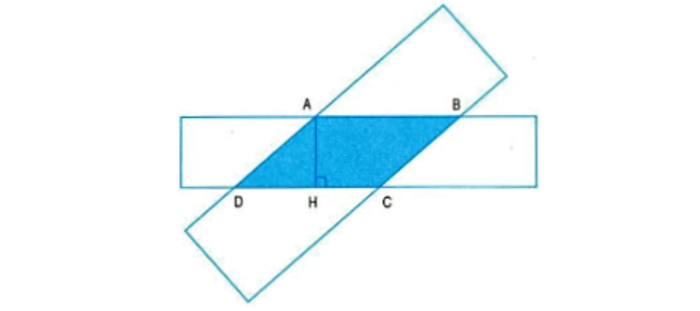
- Giải thích lý do vì sao trong hình tứ giác ABCD, các cặp cạnh đối diện lại song song.
- Đo các cạnh của hình tứ giác ABCD và kiểm tra xem các cặp cạnh đối diện có bằng nhau không.
- Biết rằng tứ giác ABCD là hình bình hành với đáy BC dài 4 cm và chiều cao AH là 2 cm. Tính diện tích của hình bình hành ABCD.
Lời giải:
a. Các cạnh AB và CD của hình chữ nhật là hai cặp cạnh đối diện nên chúng song song với nhau. Tương tự, cạnh DA và BC cũng là hai cặp cạnh đối diện và song song. Do đó, hình tứ giác ABCD có các cặp cạnh đối diện song song.
b. Sau khi đo, ta có AB = 4 cm, CD = 4 cm, DA = 3 cm và BC = 3 cm. Như vậy, AB = CD và DA = BC, cho thấy các cặp cạnh đối diện của tứ giác đều bằng nhau.
c. Diện tích của hình bình hành được tính bằng công thức 4 x 2 = 8 cm².
3. Một số bài toán về phân số cho học sinh lớp 4.
Câu 1: Một sân trường có chiều dài 120 m và chiều rộng bằng 5/6 chiều dài. Tính diện tích của sân trường.
Chiều rộng của sân trường hình chữ nhật được tính là 120 x 5/6 = 100 m.
Diện tích của sân trường hình chữ nhật là 120 x 100 = 12.000 m².
Câu 2: Với phân số 7/19, hãy xác định số tự nhiên cần thêm vào tử số và mẫu số để tạo thành một phân số mới, sao cho phân số này rút gọn thành 9/15.
Hiệu của mẫu số và tử số của phân số 7/19 là 19 - 7 = 12.
Khi cộng cùng một số vào cả tử số và mẫu số của phân số 7/19, hiệu giữa mẫu số và tử số của phân số mới vẫn là 12.
Tử số của phân số mới là 12 : 2 x 4 = 24.
Mẫu số của phân số mới được tính là 24 + 12 = 36.
Phân số mới là 24/36.
Số cần cộng vào tử số và mẫu số là 24 - 7 = 17.
Đáp số: 17.
