Đề cương ôn tập học kỳ 1 môn Toán lớp 7 mới nhất

1. Kiến thức cơ bản về đại số

- Tập hợp các số hữu tỉ: Đây là tập hợp tất cả các số có thể viết dưới dạng phân số với tử số và mẫu số là các số nguyên. Ký hiệu của tập hợp này là Q. Tất cả các số nguyên đều là số hữu tỉ vì chúng có thể viết dưới dạng phân số với mẫu số bằng 1. Tập hợp các số hữu tỉ là một tập hợp liên tục và không có khoảng cách, tức là luôn có một số hữu tỉ nằm giữa hai số hữu tỉ bất kỳ.

- Các phép toán với số hữu tỉ: Cộng, trừ, nhân và chia số hữu tỉ được thực hiện như các phép toán trên phân số. Kết quả có thể cần được đơn giản hóa và viết dưới dạng tối giản nhất.

- Lũy thừa với số mũ tự nhiên đối với số hữu tỉ: Đối với số mũ tự nhiên, quy tắc lũy thừa của số hữu tỉ áp dụng giống như quy tắc lũy thừa của số nguyên.

- Quy tắc thực hiện các phép toán và chuyển vế:

+ Thứ tự thực hiện các phép toán trong biểu thức được quy định như sau: Thực hiện phép toán trong dấu ngoặc trước tiên; sau đó thực hiện lũy thừa và căn bậc từ trái qua phải; tiếp theo là các phép nhân và chia từ trái qua phải; cuối cùng là các phép cộng và trừ từ trái qua phải.

+ Quy tắc chuyển vế khi giải phương trình hoặc bất đẳng thức bao gồm: Cộng hoặc trừ cùng một giá trị cho cả hai vế của phương trình hoặc bất đẳng thức; nhân hoặc chia cả hai vế cho cùng một giá trị khác 0; thay đổi vị trí của các vế trong phương trình hoặc bất đẳng thức.

- Số vô tỉ và căn bậc hai số học: Số vô tỉ không thể biểu diễn dưới dạng phân số. Các số vô tỉ bao gồm căn bậc hai của các số không phải là số chính phương, chẳng hạn như căn bậc hai của 2, căn bậc hai của 3, và nhiều số vô tỉ khác; căn bậc hai là phép toán tìm số có bình phương bằng một số đã cho.

- Tập hợp R của các số thực: Tập hợp R bao gồm tất cả các số thực, tức là những số có thể được biểu diễn trên trục số, bao gồm số nguyên, số hữu tỉ và số vô tỉ.

- Giá trị tuyệt đối của một số thực: Giá trị tuyệt đối của một số thực là khoảng cách của số đó từ điểm gốc trên trục số mà không xét đến dấu (+) hay (-). Nói cách khác, giá trị tuyệt đối là số dương tương ứng với số đó.

- Làm tròn và ước lượng: Đây là các phương pháp để xấp xỉ một số thực bằng cách làm tròn hoặc giới hạn số chữ số thập phân sau dấu thập phân.

- Tỉ lệ thức: Tỉ lệ thức là quy tắc toán học mô tả mối quan hệ tỷ lệ giữa các thành phần của một tập hợp số. Nó thường được thể hiện dưới dạng một phương trình với hai tỉ số bằng nhau.

- Dãy tỉ số bằng nhau: Đây là dãy số mà trong đó mỗi cặp số liên tiếp có tỉ số giống nhau. Nói cách khác, tỉ số giữa các số liên tiếp trong dãy là cố định và không thay đổi.

2. Lý thuyết về hình học

- Các góc đặc biệt và tia phân giác của góc:

+ Trong hình học, có một số góc đặc biệt rất quan trọng như góc vuông, góc nhọn, góc tù, và góc bẹt.

+ Tia phân giác của một góc là tia chia góc đó thành hai phần bằng nhau về độ lớn.

- Dấu hiệu nhận biết và đặc điểm của hai đường thẳng song song:

+ Cách nhận diện: Hai đường thẳng song song luôn giữ khoảng cách đều và không bao giờ giao nhau. Trên mặt phẳng, hai đường thẳng được coi là song song nếu góc giữa chúng bằng 0 độ hoặc 180 độ.

+ Tính chất của hai đường thẳng song song: Chúng không bao giờ cắt nhau; góc tại điểm giao là giống nhau; các cặp góc đối diện với hai đường thẳng song song là bằng nhau; nếu hai đoạn thẳng bị cắt bởi một đoạn thẳng khác sao cho các góc tạo ra bởi các đoạn thẳng đó bằng nhau, thì các đoạn thẳng này là song song.

- Tiên đề Ơ-clit: Tiên đề này dùng để định nghĩa và xác định tính chất của các đường thẳng song song. Nó phát biểu rằng: 'Với một đường thẳng và một điểm ngoài đường thẳng đó, luôn có đúng một đường thẳng đi qua điểm đó và song song với đường thẳng đã cho.'

- Định lý và chứng minh định lý:

+ Định lý là một khẳng định đã được chứng minh là đúng trong toán học. Nó là một quy tắc hay nguyên lý có giá trị trong toán học, được xây dựng dựa trên các tiên đề, quy tắc và công nhận trước đó.

+ Quy trình chứng minh định lý bao gồm việc sử dụng các lý luận và phép chứng minh để xác nhận sự đúng đắn của một định lý.

- Tổng các góc của tam giác: Tổng của ba góc trong một tam giác luôn luôn bằng 180 độ, đây là một quy tắc cơ bản trong hình học tam giác.

- Hai tam giác bằng nhau, trường hợp bằng nhau đầu tiên của tam giác:

- Đường thẳng song song: Hai đường thẳng được xem là song song khi chúng không bao giờ giao nhau, tức là không có điểm chung nào. Điều này có nghĩa là dù kéo dài đến vô tận, chúng vẫn không bao giờ cắt nhau.

+ Cách nhận diện: Hai đường thẳng là song song nếu chúng tạo ra các góc tương ứng bằng nhau khi cắt bởi một đường thẳng; hoặc nếu các góc nội tiếp với một đường thẳng cắt chúng bằng nhau.

+ Đặc điểm: Hai đường thẳng song song không bao giờ cắt nhau và luôn đi theo cùng một hướng. Các góc hình thành giữa hai đường thẳng song song với một đường cắt là các góc đối xứng, bao gồm góc tương ứng, góc nội tiếp và góc ngoại tiếp đều bằng nhau. Đồng thời, hai đường thẳng song song có cùng độ dốc hoặc độ dốc vô hạn (đường thẳng đứng).

Hãy ôn tập kỹ lưỡng trước khi giải bài tập.

3. Bài tập ôn tập học kỳ 1 môn Toán lớp 7

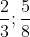
a) Xác định trong các số hữu tỉ sau, số nào là số âm và số nào là số dương.

b) Vẽ các số hữu tỉ này trên một trục số chung.

c) Tìm số đối của từng số hữu tỉ đã cho.

d) Sắp xếp các số hữu tỉ theo thứ tự giảm dần.

Bài 2: Tính toán

b) 1,2²

c) (-2,5)²

^{Bài 4: Trình bày tiên đề Ơ-clit.}

^{Bài 5: Vẽ hình theo yêu cầu, cùng với việc viết giả thiết và kết luận cho các định lý sau:}

^{a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song, thì nó cũng vuông góc với đường thẳng còn lại.}

^{b) Nếu hai đường thẳng khác biệt đều vuông góc với một đường thẳng thứ ba, thì chúng cũng sẽ song song với nhau.}

^{c) Nếu hai đường thẳng khác biệt đều vuông góc với một đường thẳng thứ ba, thì chúng cũng sẽ song song với nhau.}