Tài liệu Đề cương ôn tập môn Toán lớp 9 học kỳ 2 mới nhất
I. Các nội dung chính ôn thi học kỳ 2 môn Toán lớp 9
1. Hệ phương trình bậc nhất với hai ẩn
- Giải hệ phương trình bậc nhất với hai ẩn số.
- Giải bài toán thông qua việc thiết lập hệ phương trình.
2. Hàm số y = ax2 (với a≠0) - Phương trình bậc hai với một ẩn
- Vẽ đồ thị của hàm số y = ax2 (với a≠0).
- Bài toán liên quan đến điểm giao giữa đường thẳng và Parabol.
- Áp dụng công thức nghiệm để giải phương trình, sử dụng hệ thức Viet để xác định tham số khi hai nghiệm đáp ứng một điều kiện nhất định.
- Giải phương trình thông qua việc chuyển về dạng bậc hai, giải bài toán bằng cách thiết lập phương trình.
3. Góc liên quan đến đường tròn
- Áp dụng kiến thức về góc ở tâm, góc nội tiếp, góc giữa tiếp tuyến và dây, cùng các góc có đỉnh trong và ngoài đường tròn.
- Giải các bài toán liên quan đến tứ giác nội tiếp.
- Tính toán độ dài của đường tròn, cung tròn, cùng diện tích của hình tròn và hình quạt tròn.
II. Bài tập ôn thi môn Toán lớp 9 học kỳ 2
Dạng 1 : Giải hệ phương trình và phương trình
Bài 1: Giải hệ phương trình sau:
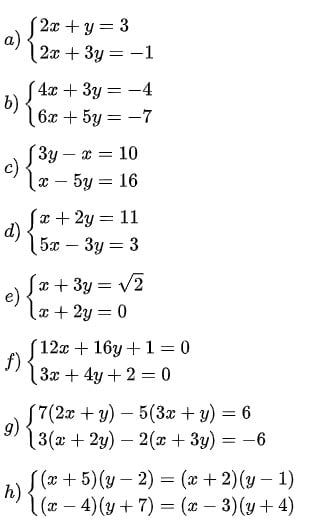
Bài 2: Giải các phương trình sau đây:
a) x2 - x - 20 = 0
b) 3x2 + 8x + 4 = 0
c) 5x2 - 6x - 8 = 0
d) -2x2 + 3x + 5 = 0
e) x
f) 3x2 - 7x + 2 = 0
k) 4x4 + 7x2 - 2 = 0
l) x4 - 13x2 + 36 = 0
m) x4 + 7x2 - 8 = 0
n) 2x4 + 5x2 + 2 = 0
o) (2x + 1)4 - 8(2x + 1)2 - 9 = 0
...............
Dạng 2: Giải bài toán bằng cách thiết lập phương trình hoặc hệ phương trình
Bài 1: Một chiếc ô tô di chuyển từ A đến B trong một khoảng thời gian nhất định. Nếu xe chạy với tốc độ 35 km/h thì đến muộn 2 giờ. Nếu xe chạy với tốc độ 50 km/h thì đến sớm 1 giờ. Tìm quãng đường AB và thời gian dự định đi ban đầu.
Bài 2: Một người điều khiển xe máy di chuyển từ A đến B, khoảng cách là 120 km với tốc độ dự kiến. Sau khi đi hết quãng đường AB, người đó tăng tốc độ thêm 10 km/h cho phần còn lại. Tìm vận tốc dự định và thời gian di chuyển trên đường, biết rằng người đó đến B sớm hơn 24 phút so với dự định.
Bài 3: Một canô đi từ bến A đến bến B với tốc độ 30 km/h và trở lại A từ B. Thời gian di chuyển xuôi dòng ít hơn thời gian di chuyển ngược dòng 1 giờ 20 phút. Tính khoảng cách giữa hai bến A và B, với vận tốc dòng nước là 5 km/h và vận tốc của canô khi xuôi và ngược là như nhau.
Bài 4: Một canô di chuyển xuôi một đoạn sông dài 90 km rồi ngược trở lại 36 km. Thời gian di chuyển xuôi dòng nhiều hơn thời gian di chuyển ngược dòng 2 giờ, và tốc độ khi xuôi dòng nhanh hơn khi ngược dòng 6 km/h. Tìm vận tốc của canô khi xuôi và ngược dòng.
Bài 5: Trong đợt dịch SARS-CoV-2, một phân xưởng dự định sản xuất 10.000 khẩu trang trong thời gian quy định. Sau khi cải tiến kỹ thuật tăng năng suất thêm 100 khẩu trang/giờ, phân xưởng hoàn thành sớm hơn 5 giờ so với dự định. Tính thời gian ban đầu dự định để sản xuất 10.000 khẩu trang.
Bài 6: Hai thợ cùng làm một công việc trong 7 giờ 12 phút thì xong. Nếu người thứ nhất làm trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai chỉ hoàn thành được ¾ công việc. Tính thời gian một người làm xong công việc đó.
Bài 7: Nếu vòi A chảy nước trong 2 giờ và vòi B chảy trong 3 giờ thì đầy hồ. Nếu vòi A hoạt động trong 3 giờ và vòi B trong 1 giờ 30 phút thì cũng đầy hồ. Tìm thời gian mỗi vòi cần để làm đầy hồ nếu hoạt động một mình.
Bài 8: Trong tháng giêng, hai tổ sản xuất tổng cộng 720 chi tiết máy. Sang tháng hai, tổ I vượt chỉ tiêu 15% và tổ II vượt chỉ tiêu 12%, tổng sản xuất được 819 chi tiết máy. Xác định số chi tiết máy mà mỗi tổ sản xuất được trong tháng giêng.
Bài 9: Năm ngoái, tổng dân số của hai tỉnh A và B là 4 triệu người. Năm nay, dân số tỉnh A tăng 1,2% và tỉnh B tăng 1,1%, tổng dân số của cả hai tỉnh hiện là 4.045.000 người. Tính số dân của mỗi tỉnh trong năm ngoái và năm nay.
Bài 10: Một hình chữ nhật có chu vi 280m. Nếu giảm chiều dài 2m và tăng chiều rộng 3m thì diện tích tăng thêm 144m2. Tìm các kích thước của hình chữ nhật.
Bài 11: Tìm một số tự nhiên hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị 2 đơn vị và nếu thêm chữ số hàng chục vào bên phải số đó, số mới lớn hơn số ban đầu 682.
Bài 12: Tìm một số tự nhiên hai chữ số, biết rằng tổng hai chữ số của số đó là 10 và tích của chúng nhỏ hơn số đó 12 đơn vị.
Bài 13: Trong một tam giác vuông, cạnh huyền dài 5 cm và diện tích là 6 cm². Xác định độ dài của hai cạnh góc vuông.
Bài 14: Có hai ngăn sách, trong đó số sách ở ngăn trên là 1/5 số sách ở ngăn dưới. Nếu thêm 25 cuốn sách vào ngăn trên và bớt 15 cuốn từ ngăn dưới, số sách ở ngăn trên sẽ bằng 2/3 số sách ở ngăn dưới. Tìm số sách ở mỗi ngăn ban đầu.
Bài 15: Một phòng học có 320 ghế được xếp thành nhiều dãy bằng nhau. Nếu số dãy tăng thêm 2, tổng số ghế trong phòng sẽ là 396. Tính số dãy ghế và số ghế mỗi dãy ban đầu.
Bài 16: Hai xí nghiệp có kế hoạch sản xuất tổng cộng 360 dụng cụ. Xí nghiệp I đã vượt kế hoạch 12% và xí nghiệp II đã vượt kế hoạch 10%, làm tổng cộng 400 dụng cụ. Tính số dụng cụ mà mỗi xí nghiệp phải sản xuất theo kế hoạch.
Bài tập 17
Hai ô tô xuất phát cùng lúc từ A đến B, khoảng cách 300 km. Ô tô đầu tiên chạy nhanh hơn ô tô thứ hai 10 km/h và đến B sớm hơn 1 giờ. Xác định tốc độ của mỗi ô tô.
Bài tập 18
An và Bình cùng may khẩu trang để hỗ trợ trong dịch Covid-19, hoàn thành trong 2 ngày. Nếu An làm trong 4 ngày rồi nghỉ và Bình làm tiếp 1 ngày, công việc cũng hoàn thành. Tính thời gian mỗi người cần làm việc một mình để hoàn thành công việc.
Bài tập 19
Hai nhóm công nhân được giao nhiệm vụ đắp đê để ngăn ngừa triều cường. Nếu cả hai nhóm làm việc cùng nhau, công việc sẽ hoàn thành trong 6 ngày. Tuy nhiên, nếu làm riêng, đội một sẽ mất nhiều thời gian hơn đội hai 9 ngày. Câu hỏi đặt ra là mỗi đội sẽ hoàn thành công việc trong bao nhiêu ngày nếu làm một mình?
Bài tập 20
Một nhóm học sinh dự định chế tạo 360 chiếc mũ chắn giọt bắn trong một khoảng thời gian nhất định để hỗ trợ các địa phương trong công tác phòng, chống dịch COVID-19. Thực tế, nhóm hoàn thành vượt mức 12 chiếc mũ mỗi ngày so với kế hoạch và vì vậy, nhóm hoàn tất công việc trước dự định hai ngày và làm thêm được 4 chiếc mũ. Hãy tính số mũ nhóm dự định làm mỗi ngày.
Bài tập 21
Một đội xe dự kiến chở một số tấn hàng. Để đảm bảo an toàn, đội xe được bổ sung thêm một xe, và khi đó số tấn hàng mỗi xe chở giảm so với kế hoạch ban đầu. Tính số tấn hàng mỗi xe dự định chở ban đầu, với điều kiện số tấn hàng mỗi xe thực tế chở là bằng nhau.
Dạng 3: Các bài toán liên quan đến phương trình bậc hai với một ẩn
Bài 1: Xét phương trình bậc hai x² – 2(m + 1)x + m – 4 = 0 (1)
a) Tìm nghiệm của phương trình (1) khi m = 1
b) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt cho mọi giá trị của m.
c) Chứng minh rằng biểu thức A = x₁(1 – x₂) + x₂(1 – x₁) không phụ thuộc vào giá trị của m.
Bài 2: Xét phương trình x² – 2(m + 1)x + 3(2m – 1) = 0 (1)
a) Xác định giá trị của m để phương trình (1) có hai nghiệm phân biệt x₁ và x₂.
b) Xây dựng mối liên hệ giữa x₁ và x₂ sao cho không phụ thuộc vào giá trị của m.
c) Tìm giá trị của m để biểu thức A = x₁² + x₂² đạt giá trị nhỏ nhất.

