1. Bộ đề ôn tập 1
Bài 1. Đặt đa thức A(x) = –11x^5 + 4x – 12x^2 + 11x^5 + 13x^2 – 7x + 2.
a) Rút gọn và sắp xếp đa thức A(x) theo thứ tự số mũ giảm dần của biến, sau đó xác định bậc và hệ số cao nhất của đa thức.
b) Tìm đa thức M(x) sao cho M(x) = A(x) × B(x), với B(x) = x – 1.
c) Xác định nghiệm của đa thức A(x).
Hướng dẫn giải chi tiết
a) Chúng ta có:
A(x) = –11x^5 + 4x – 12x^2 + 11x^5 + 13x^2 – 7x + 2
= x^2 – 3x + 2.
Đa thức A(x) có bậc là 2 và hệ số bậc cao nhất là 1.
b) M(x) = A(x) × B(x)
= (x^2 – 3x + 2) × (x – 1)
= x × (x^2 – 3x + 2) – 1 × (x^2 – 3x + 2)
= x^3 – 3x^2 + 2x – x^2 + 3x – 2
= x^2 – 4x + 2.
c) A(x) = 0
x^2 – 3x + 2 = 0
x^2 – x – 2x + 2 = 0
x(x – 1) – 2(x – 1) = 0
(x – 1)(x – 2) = 0
x = 1 hoặc x = 2.
Do đó, đa thức A(x) có các nghiệm x ∈ {1, 2}.
Bài 2. Ba đội công nhân cùng thực hiện chuyển một khối lượng gạch giống nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba hoàn thành công việc lần lượt là 2 giờ, 3 giờ, và 4 giờ. Tính số công nhân của mỗi đội, biết rằng đội ba có ít hơn đội hai 5 người và năng suất lao động của các công nhân là như nhau.
Giải chi tiết:
Đặt số công nhân của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là x, y, và z.
Do đội ba có ít công nhân hơn đội hai là 5 người, nên y – z = 5.
Với cùng khối lượng công việc, số công nhân và thời gian hoàn thành công việc của mỗi đội là hai đại lượng tỷ lệ nghịch với nhau.
Vì vậy, ta có tỉ lệ 2x = 3y = 4z, suy ra x/12 = y/13 = z/14.
Áp dụng tính chất của dãy tỷ lệ bằng nhau, ta có:
x/12 = y/13 = z/14 = (y – z)/(13 – 14) = 5/11 = 12/60.
Từ đó suy ra x = 60/12 = 30, y = 60/13 = 20, z = 60/14 = 15.
Do đó, số công nhân của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là 30 người, 20 người, và 15 người.
Bài 3. Chọn ngẫu nhiên một số từ tập hợp M = {2; 3; 5; 6; 8; 9}.
a) Trong các biến cố sau, biến cố nào là chắc chắn? Biến cố nào là không thể xảy ra và biến cố nào là biến cố ngẫu nhiên?
A: “Số được chọn là số nguyên tố”
B: “Số được chọn là số có một chữ số”
C: “Số được chọn là số tròn chục”
b) Tính xác suất xảy ra của biến cố A.
Lời giải chi tiết:
a) Tập hợp M bao gồm cả số nguyên tố lẫn hợp số, do đó biến cố A thuộc loại biến cố ngẫu nhiên.
Tất cả các số trong tập hợp M đều là số có một chữ số, vì vậy biến cố B là biến cố chắc chắn.
Tập hợp M không chứa số nào là số tròn chục, nên biến cố C là biến cố không thể xảy ra.
b) Trong tập hợp M có 6 số, trong đó có 3 số nguyên tố là 2, 3 và 5.
Xác suất của biến cố A được tính là: 3/6 = 1/2.
Bài 4. Trong tam giác vuông ABC tại đỉnh A, BD là đường phân giác với D thuộc cạnh AC. Từ điểm D, kẻ đường thẳng DH vuông góc với BC.
a) Chứng minh rằng tam giác ABD bằng tam giác HBD.
b) So sánh độ dài của AD và DC.
c) Xét điểm K là giao điểm của đường thẳng AB với DH, và I là trung điểm của đoạn thẳng KC. Chứng minh rằng ba điểm B, D, I nằm trên cùng một đường thẳng.
Lời giải chi tiết
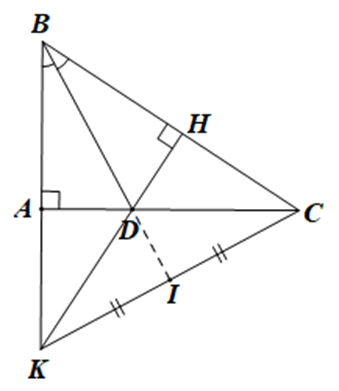
a) Xem xét tam giác ΔABD và ΔHBD có các góc:
BHD^=BAD^=90°,
BD là cạnh chung của hai tam giác,
ABD^=HBD^ (vì BD là tia phân giác của góc ABD^).
Do đó, ta có ΔABD = ΔHBD (cạnh huyền – góc nhọn).
b) Từ ΔABD = ΔHBD (theo câu a) suy ra rằng AD = HD (hai cạnh tương ứng)
Xem xét tam giác ΔDHC vuông tại H, với DC là cạnh huyền nên DC là cạnh dài nhất
Do đó, ta có DC > HD và vì vậy DC > AD.
c) Trong tam giác ΔBKC, CA vuông góc với BK, KH vuông góc với BC, và CA cắt KH tại D
Vì thế, D là trực tâm của tam giác DBKC, do đó BD vuông góc với KC (1)
Gọi J là điểm chung của BD và KC.
Xem xét tam giác ΔBKJ và ΔBCJ có:
BJK^=BJC^=90°
BJ là cạnh chung của hai tam giác,
KBJ^=CBJ^ (do BJ là tia phân giác của góc ABD^).
Vì vậy, ΔBKJ = ΔBCJ (cạnh góc vuông – góc nhọn kề)
Từ đó, ta có KJ = CJ (các cạnh tương ứng).
Vì vậy, J là trung điểm của KC.
Do I là trung điểm của KC, nên I và J trùng nhau.
Như vậy, ba điểm B, D, I nằm trên một đường thẳng.
Bài 5. Xác định các giá trị nguyên của n để 2n² – n + 2 chia hết cho 2n + 1.
Giải chi tiết
Tiến hành chia đa thức 2n² – n + 2 cho đa thức 2n + 1 như sau:
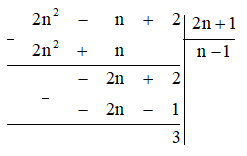
Để 2n² – n + 2 chia hết cho 2n + 1, ta cần (2n + 1) thuộc tập hợp Ư(3) = {1; ‒1; 3; ‒3}.
Dưới đây là bảng kết quả:
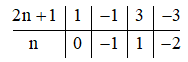
Do đó n thuộc tập hợp {–2; –1; 0; 1}.
2. Đề ôn tập số 2
Bài 1. (1,0 điểm) Tìm giá trị của x, biết rằng:
a) x − 13 = 12;
b) Giải phương trình 5x(x – 3) = (x – 2)(5x – 1) – 5.
Chi tiết giải
a) x − 13 = 12
2.(x – 1) = 3.1
2x – 2 = 3
2x = 5
x = 2.5
Vậy, x = 2.5.
b) Giải phương trình 5x(x – 3) = (x – 2)(5x – 1) – 5
5x^2 – 15x = 5x^2 – x – 10x + 2 – 5
–4x = –3
x = 3/4
Vậy, x = 3/4.
Bài 2. Xét hai đa thức A(x) = x – 2x^2 + 3x^5 + x^4 + x + x^2;
B(x) = –2x^2 + x – 2 – x^4 + 3x^2 – 3x^5.
a) Rút gọn và sắp xếp hai đa thức theo thứ tự giảm dần của các lũy thừa.
b) Tìm đa thức M(x) sao cho B(x) = A(x) + M(x). Xác định bậc và hệ số cao nhất của M(x).
c) Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).
Lời giải chi tiết
a) A(x) = x – 2x^2 + 3x^5 + x^4 + x + x^2
= 3x^5 + x^4 – x^2 + 2x
B(x) = –2x^2 + x – 2 – x^4 + 3x^2 – 3x^5
= –3x^5 – x^4 + x^2 + x – 2
b) B(x) = A(x) + M(x)
Do đó, M(x) = B(x) – A(x)
M(x) = (–3x^5 – x^4 + x^2 + x – 2) – (3x^5 + x^4 – x^2 + 2x)
= –3x^5 – x^4 + x^2 + x – 2 – 3x^5 – x^4 + x^2 – 2x
= –6x^5 – 2x^4 + 2x^2 – x – 2
Đa thức M(x) có bậc là 5 và hệ số cao nhất là –6.
c) A(x) = N(x) – B(x)
Do đó N(x) = A(x) + B(x)
N(x) = (3x^5 + x^4 – x^2 + 2x) + (–3x^5 – x^4 + x^2 + x – 2)
= 3x^5 + x^4 – x^2 + 2x – 3x^5 – x^4 + x^2 + x – 2
= –x – 2
Vậy N(x) = 0
Do đó, –x – 2 dẫn đến x = –2
Vậy nghiệm của đa thức N(x) là x = –2
Bài 3. Ba phân xưởng in tổng cộng có 47 máy in, mỗi phân xưởng được phân công in một số trang bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày, và phân xưởng thứ ba trong 5 ngày. Hãy xác định số máy in của từng phân xưởng.
Lời giải chi tiết:
Gọi x, y, z lần lượt là số máy in của các phân xưởng thứ nhất, thứ hai, và thứ ba.
Tổng số máy in của ba phân xưởng là x + y + z = 47
Vì thời gian hoàn thành công việc tỷ lệ nghịch với số máy in, ta có: x/3 = y/4 = z/5
Áp dụng tính chất của dãy tỷ số bằng nhau, ta có: x/3 = y/4 = z/5 = (x + y + z) / (3 + 4 + 5) = 47 / 12 = 60
Do đó, x = 60 × 1/3 = 20; y = 60 × 1/4 = 15; z = 60 × 1/5 = 12
Vậy số máy in của ba phân xưởng lần lượt là 20, 15, và 12.
Bài 4. Trong một hộp kín, có 5 quả bóng với kích thước và khối lượng giống nhau, được đánh số 5, 10, 15, 20, 25. Khi rút ngẫu nhiên một quả bóng từ hộp, xem xét các sự kiện sau:
A: “Quả bóng rút ra có số là số nguyên tố”;
B: “Quả bóng rút ra có số chia hết cho 5”;
C: “Quả bóng rút ra có số chia hết cho 6”;
D: “Quả bóng rút ra có số là số tròn chục”.
a) Xác định biến cố nào trong số các biến cố trên là chắc chắn, và biến cố nào là không thể xảy ra.
b) Tính xác suất cho các biến cố A và D.
Lời giải chi tiết
a) Biến cố B là biến cố chắc chắn, trong khi biến cố C là biến cố không thể xảy ra.
b) Do tất cả 5 quả bóng có kích thước và khối lượng giống nhau, nên khả năng rút được mỗi quả bóng là như nhau.
• Trong số 5 quả bóng được đánh số 5; 10; 15; 20; 25, chỉ có quả bóng ghi số 5 là số nguyên tố. Vì vậy, xác suất của biến cố A là P(A) = 1/5.
• Trong số 5 quả bóng được đánh số 5; 10; 15; 20; 25, có 2 quả bóng ghi số tròn chục là 10 và 20. Do đó, xác suất của biến cố D là P(D) = 2/5.
Bài 5. (2,5 điểm) Cho tam giác ABC vuông tại A (với AB < AC). Tại cạnh BC, lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, và cắt tia BA tại N.
a) So sánh các góc trong tam giác ABC.
b) Chứng minh rằng ΔDAB ≅ ΔDDBM. Từ đó, suy ra MA = MD.
c) Tam giác MNC thuộc loại tam giác nào? Giải thích lý do.
d) Gọi I là trung điểm của CN. Chứng minh rằng ba điểm B, M, I nằm trên cùng một đường thẳng.
Lời giải chi tiết
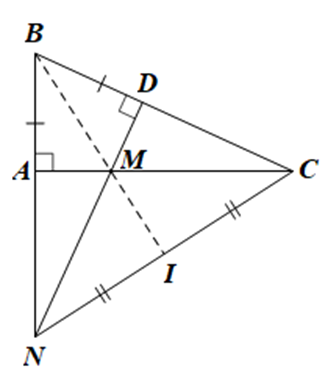
a) Tam giác ABC là tam giác vuông tại A, nên cạnh huyền BC là cạnh dài nhất.
Vì AB < AC nên AB < AC < BC.
Do đó, ta có C^ < B^ < A^ (theo quan hệ giữa các góc và cạnh đối diện trong tam giác).
b) Xem xét hai tam giác ΔABM và ΔDBM với các điều kiện sau:
Góc BAM^ = góc BDM^ = 90°;
BA = BD (theo giả thiết).
BM là cạnh chung giữa hai tam giác.
Vì vậy, ΔABM đồng dạng với ΔDBM (cạnh huyền và cạnh góc vuông).
Suy ra MA = MD (các cạnh tương ứng).
c) Xem xét hai tam giác ΔANM và ΔDCM với các điều kiện sau:
Góc NAM^ = góc CDM^ = 90°;
MA = MD (theo chứng minh ở câu b).
Góc AMN^ bằng góc DMC^ (hai góc đối đỉnh).
Do đó, ΔANM đồng dạng với ΔDCM (cạnh góc vuông và góc nhọn kề).
Suy ra MN = MC (các cạnh tương ứng).
Vì MN = MC, tam giác MNC là tam giác cân tại M.
d) Với ΔMNC là tam giác cân tại M và I là trung điểm của NC, nên MI là đường trung tuyến của ΔMNC.
Khi đó, MI cũng là đường cao của tam giác DMNC, tức là MI ⊥ NC (1).
Trong ΔBNC, hai đường cao CA và ND giao nhau tại M, nên M là trực tâm của tam giác DBNC.
Suy ra BM ⊥ NC (2).
Từ (1) và (2), ta kết luận ba điểm B, M, I thẳng hàng.
Bài 6. (0,5 điểm) Tìm giá trị nguyên dương của x để đa thức x³ – 3x² – 3x – 1 chia hết cho đa thức x² + x + 1.
Lời giải chi tiết:
Thực hiện phép chia đa thức như sau: Để đa thức x³ – 3x² – 3x – 1 chia hết cho x² + x + 1 thì cần có điều kiện 3 ⋮ (x² + x + 1).
.PNG)
Tức là x² + x + 1 thuộc Ư(3) = {–3; 3; –1; 1}.
Vì x > 0 nên x² + x + 1 > 1.
Vì vậy, x² + x + 1 = 3
x² + x – 2 = 0
x² – x + 2x – 2 = 0
x(x – 1) + 2(x – 1) = 0
(x – 1)(x + 2) = 0
Vì vậy, x = 1 là nghiệm hợp lệ, còn x = –2 thì không thỏa mãn.
Do đó, với x = 1, đa thức x³ – 3x² – 3x – 1 chia hết cho đa thức x² + x + 1.
