1. Đề thi giữa kì 2 môn Toán lớp 7 (Đề số 1)
Phòng Giáo dục và Đào tạo...
Trường THCS ...
Đề thi Giữa kì 2
Năm học 2023 - 2024
Môn: Toán lớp 7
Thời gian làm bài: phút (không bao gồm thời gian phát đề)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Hãy khoanh tròn vào câu trả lời đúng duy nhất cho mỗi câu hỏi dưới đây:
Câu 1. Tỉ số 1,2 : 1,35 có thể chuyển đổi thành tỉ số giữa các số nguyên là:
A. 50 : 81;
B. 8 : 9;
C. 5 : 8;
D. 1 : 10.
Câu 2. Nếu y tỉ lệ nghịch với x với hệ số tỉ lệ là a và khi x = –2 thì y = 4, thì hệ số a là bao nhiêu?
A. –2;
B. –6;
C. –8;
D. –4.
Câu 3. Với hệ phương trình 7x = 4y và y – x = 24, giá trị của x và y là:
A. x = −56, y = −32;
B. x = 32, y = 56;
C. x = 56, y = 32;
D. x = 56, y = −32.
Câu 4. Biểu thức đại số diễn tả “Bình phương của tổng hai số x và y” là:
A. x2 – y2;
B. x + y;
C. x2 + y2;
D. (x + y)2
Câu 5. Hệ số tự do trong đa thức M = 8x2 – 4x + 3 – x5 là:
A. 1;
B. 4;
C. 3;
D. 5.
Câu 6. Hai tam giác được coi là bằng nhau khi nào?
A. Khi hai tam giác có ba cặp cạnh tương ứng bằng nhau;
B. Khi hai tam giác có ba cặp góc tương ứng bằng nhau;
C. Khi hai tam giác có cả ba cặp cạnh và ba cặp góc tương ứng bằng nhau;
D. Khi hai tam giác có hai cạnh bằng nhau.
Câu 7. Trong tam giác MNP với MN < MP và MD ⊥ NP, khẳng định nào sau đây là chính xác?
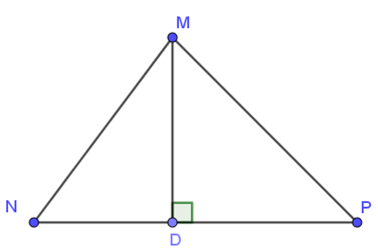
A. DN = DP;
B. MD < MP;
C. MD > MN;
D. MN = MP.
Câu 8. Hoàn thành câu sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
A. Trung trực;
B. Giao điểm;
C. Trọng tâm;
D. Trung điểm.
II. Bài tập tự luận (8.0 điểm)
Câu 1. (1,5 điểm) Giải các bài toán sau đây:
a) x/6 = -3/4
b) 5/x = 15/-20
Bài 2. (2,0 điểm)
a. Tìm hai số a và b sao cho 2a = 5b và 3a + 4b = 46
b. Xác định ba số a, b, c với tỷ lệ a : b : c = 2 : 4 : 5 và a + b - c = 3
Bài 3. (1,5 điểm) Trong chiến dịch quyên góp sách hỗ trợ vùng cao, số sách quyên góp được của ba lớp 7A, 7B, 7C tỷ lệ với các số 5; 6; 8. Tính tổng số sách quyên góp của ba lớp, biết số sách lớp 7C quyên góp nhiều hơn lớp 7A là 24 quyển.
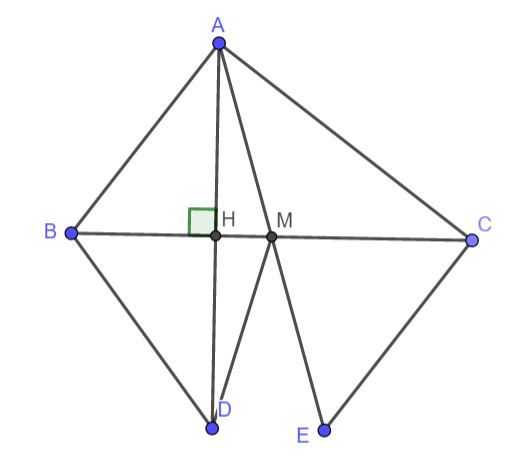
Bài 4. (3,0 điểm) Trong tam giác ABC (AB < AC), M là trung điểm của BC. Trên tia đối của tia MA, chọn điểm E sao cho AM = EM.
a. Chứng minh rằng ΔAMB đồng dạng với ΔMCE
b. Vẽ AH vuông góc với BC từ A. Trên tia đối của tia HA, chọn điểm D sao cho HA = HD. Chứng minh rằng CE = BD
c. Tam giác AMD là loại tam giác gì? Giải thích lý do.
Đáp án cho đề thi giữa học kỳ 2 môn Toán lớp 7 phiên bản mới nhất năm học 2023 - 2024
I. Trắc nghiệm khách quan (2.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5
| 6 | 7 | 8 |
| Đáp án | B | C | B | D | C | C | B | D |
II. Phần tự luận (8.0 điểm)
Bài 1. (1,5 điểm) Xác định giá trị số hữu tỉ x trong các tỉ lệ thức sau:
a. x/6 = -3/4
x = (-3) x 6 / 4
x = -9/2
Do đó, x = -9/2
b. 5/x = 15/(-20)
x = 5 x (-20) / 15
x = -20/3
Vậy x = -20/3
Bài 2. (2,0 điểm)
a) Ta có: 2a = 5b
→ a/5 = b/2
Đồng thời, a/5 = 3a/15; b/2 = 4b/8
→ 3a/15 = 4b/8 = 3a + 4b / 15 + 8 = 46 / 23 = 2
→ 3a = 2 x 15 = 30
→ a = 10
4b = 2 x 8 = 16
→ b = 4
b) a : b : c = 2 : 4 : 5
→ a/2 = b/4 = c/5 = (a + b - c) / (2 + 4 - 5) = 3 / 1 = 3
→ a = 2 x 3 = 6
b = 4 x 3 = 12
c = 5 x 3 = 15
Bài 3. (1,5 điểm)

Bài 4 (3,0 điểm)
2. Đề thi giữa học kỳ 2 môn Toán lớp 7 (Đề số 2)
Phòng Giáo dục và Đào tạo...
Trường THCS ...
Đề thi giữa học kỳ 2
Năm học 2022 - 2023
Môn: Toán lớp 7
Thời gian làm bài: phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Vui lòng chọn phương án đúng nhất cho từng câu hỏi dưới đây:
Câu 1. Đổi tỉ số 1,25 : 3,45 thành tỉ số giữa các số nguyên sẽ là
A. 12,5 : 34,5;
B. 29 : 65;
C. 25 : 69;
D. 1 : 3.
Câu 2. Nếu 7x = 4y và y – x = 24, giá trị của x và y sẽ là
A. x = −56, y = −32;
B. x = 32, y = 56;
C. x = 56, y = 32;
D. x = 56, y = −32.
Câu 3. Nếu y tỉ lệ thuận với x với hệ số tỉ lệ k = 2 và khi x = –3 thì giá trị của y là bao nhiêu?
A. –6;
B. 0;
C. –9;
D. –1.
Câu 4. Xét hai đại lượng x và y tỉ lệ nghịch với nhau. Khi x = –12, y = 8. Tính y khi x = 3 là:
A. –32;
B. 32;
C. –2;
D. 2.
Câu 5. Biểu thức đại số diễn tả “Bình phương của tổng hai số x và y” là:
A. x2 – y2;
B. x + y;
C. x2 + y2;
D. (x + y)2.
Câu 6. Hệ số tự do của đa thức M = 8x2 – 4x + 3 – x5 là:
A. 1;
B. 4;
C. 3;
D. 5.
Câu 7. Với các đa thức P(x) = 6x3 − 3x2 − 2x + 4 và G(x) = 5x2 − 7x + 9, giá trị của P(x) − G(x) là:
A. x2 − 9x + 13;
B. 6x3 − 8x2 + 5x − 5;
C. x3 − 8x2 + 5x − 5;
D. 5x3 − 8x2 + 5x + 13.
Câu 8. Kết quả của phép nhân (5x − 2)(2x + 1) là đa thức nào dưới đây?
A. 10x2 − 3x − 2;
B. 10x2 − x + 4;
C. 10x2 + x − 2;
D. 10x2 − x − 2.
Câu 10. Xét tam giác MNP với MN < MP và MD ⊥ NP. Khẳng định nào dưới đây là đúng?
A. DN = DP;
B. MD < MP;
C. MD > MN;
D. MN = MP.
Câu 11. Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào không thể tạo thành tam giác?
A. 15cm; 25cm; 10cm;
B. 5cm; 4cm; 6cm;
C. 15cm; 18cm; 20cm;
D. 11cm; 9cm; 7cm.
Câu 12. Trong tam giác nhọn ΔABC, hai đường trung tuyến AM và BN cắt nhau tại O. Khẳng định nào sau đây là sai?
A. AO = 2/3AM;
B. OM = 1/3AM;
C. AO = 2/3BN;
D. NO = 1/3BN.
II. Phần tự luận
Bài 1. (1,0 điểm) Ba lớp 7A, 7B, 7C được phân công trồng tổng cộng 120 cây để làm xanh khu đồi. Tính số cây mà mỗi lớp trồng, biết rằng số cây của ba lớp này tỉ lệ với các số 7; 8; 9.
Bài 2. (2,0 điểm) Cho hai đa thức P(x) = x^3 – 2x^2 + x – 2 và Q(x) = 2x^3 – 4x^2 + 3x – 6.
a) Tính P(x) – Q(x).
b) Chứng minh rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 3. (2,0 điểm) Xét tam giác ABC với D là trung điểm của AC. Trên đoạn BD, chọn điểm E sao cho BE = 2ED. Điểm F nằm trên tia đối của tia DE sao cho BF = 2BE. Gọi K là trung điểm của CF và G là điểm giao của EK với AC. Chứng minh rằng G là trọng tâm của tam giác EFC.
Bài 4. (0,5 điểm) Xét tỉ lệ thức a/b = c/d. Chứng minh rằng (a−2b)/b = (c−2d)/d.
Đáp án cho đề thi giữa học kì 2 môn toán lớp 7 năm học 2023 - 2024
I. Phần trắc nghiệm (3.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Đáp án | C | B | A | A | D | C | B | C | C | B | A | C |
II. Phần tự luận (7.0 điểm)
Bài 1. (1,0 điểm)
Gọi số cây trồng của ba lớp 7A, 7B, 7C lần lượt là x, y, z (với x, y, z > 0). Tổng số cây trồng là 120 cây, do đó x + y + z = 120. Tỉ lệ số cây trồng của ba lớp này là 7:8:9, tức là x/7 = y/8 = z/9. Áp dụng tỉ số, ta có x/7 = y/8 = z/9 = (x + y + z)/(7 + 8 + 9) = 120/24 = 5. Do vậy, x = 5 × 7 = 35, y = 5 × 8 = 40, z = 5 × 9 = 45. Vậy số cây trồng của ba lớp 7A, 7B, 7C lần lượt là 35, 40, và 45 cây.
Bài 2. (2,0 điểm)
a) Tính P(x) – Q(x):
= (x^3 – 2x^2 + x – 2) – (2x^3 – 4x^2 + 3x – 6)
= x^3 – 2x^2 + x – 2 – 2x^3 + 4x^2 – 3x + 6
= (x^3 – 2x^3) + (4x^2 – 2x^2) + (x – 3x) + (6 – 2)
= – x^3 + 2x^2 – 2x + 4.
Vậy P(x) – Q(x) = – x^3 + 2x^2 – 2x + 4.
b) Thay x = 2 vào đa thức P(x):
P(2) = 2^3 – 2 × 2^2 + 2 – 2
= 8 – 2 × 4 + 2 – 2
= 8 – 8 + 2 – 2 = 0;
Thay x = 2 vào đa thức Q(x):
Q(2) = 2 × 2^3 – 4 × 2^2 + 3 × 2 – 6
= 2 × 8 – 4 × 4 + 6 – 6
= 16 – 16 + 6 – 6 = 0.
Do đó, x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 3. (1,5 điểm)
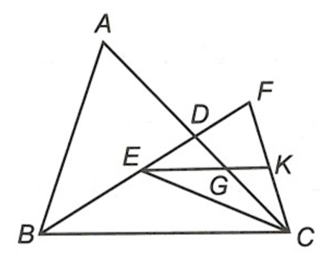
Từ BF = 2BE suy ra BE = EF.
Vì BE = 2ED nên EF cũng bằng 2ED.
Do đó, D là trung điểm của EF.
Như vậy, CD là đường trung tuyến của tam giác EFC.
K là trung điểm của CF nên EK cũng là đường trung tuyến của tam giác EFC.
Tam giác EFC có hai đường trung tuyến CD và EK giao nhau tại G, do đó G chính là trọng tâm của tam giác EFC.
Bài 5 (0,5 điểm)