1. Đề thi giữa kỳ 2 môn Toán lớp 7 sách Chân trời sáng tạo
Đề thi giữa kỳ 2 môn Toán lớp 7
PHÒNG GD-ĐT …
TRƯỜNG THCS…
ĐỀ KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022-2023
MÔN TOÁN – KHỐI 7
Thời gian làm bài: 90 phút
PHẦN TRẮC NGHIỆM (2,0 điểm) Chọn đáp án chính xác cho mỗi câu hỏi dưới đây:
Câu 1. Thay tỉ số 1,25 : 3,45 bằng tỉ số giữa các số nguyên tương ứng ta nhận được
A. 12,5 : 34,5; B. 29 : 65; C. 25 : 69; D. 1 : 3.
Câu 2. Biết y tỉ lệ thuận với x với hệ số tỉ lệ k = 2. Khi x = –3 thì y có giá trị là bao nhiêu?
A. –6; B. 0; C. –9; D. –1.
Câu 3. Nếu x và y là hai đại lượng tỉ lệ nghịch và khi x = –12 thì y = 8. Vậy khi x = 3 thì y sẽ là
A. –32; B. 32; C. –2; D. 2.
Câu 4. Xem hình dưới đây: Giá trị của x là
A. 18°; B. 72°; C. 36°; D. Không thể xác định.
Câu 5. Định nghĩa hai tam giác bằng nhau là
A. Hai tam giác có ba cặp cạnh tương ứng bằng nhau;
B. Hai tam giác có ba cặp góc tương ứng trùng khớp;
C. Hai tam giác có ba cặp cạnh và ba cặp góc tương ứng bằng nhau;
D. Hai tam giác có hai cạnh tương ứng bằng nhau.
Câu 6. Nếu một tam giác cân có hai góc đáy là 40°, thì góc ở đỉnh sẽ là
A. 50°; B. 40°; C. 140°; D. 100°.
Câu 7. Trong tam giác MNP với MN < MP và MD ⊥ NP, khẳng định nào sau đây là chính xác?
A. DN = DP; B. MN = MP; C. MD > MN; D. MD < MP.
Câu 8. Điền từ còn thiếu: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó.”
A. Trung điểm; B. Giao điểm; C. Trọng tâm; D. Trung trực.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1,5 điểm) Tìm giá trị của x trong các tỉ lệ thức dưới đây:
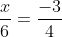
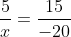

Bài 2. (2,0 điểm)
a. Xác định hai số a và b sao cho 2a = 5b và 3a + 4b = 46
b. Xác định ba số a, b, c biết rằng tỉ số a : b : c = 2 : 4 : 5 và a + b - c = 3
Bài 3. (1,5 điểm) Trong hoạt động quyên góp sách để hỗ trợ các bạn ở vùng cao, số sách mà ba lớp 7A, 7B, 7C quyên góp tỷ lệ với các số 5, 6, 8. Tính tổng số sách của cả ba lớp, biết rằng lớp 7C quyên góp nhiều hơn lớp 7A là 24 quyển.
Bài 4. (3,0 điểm) Xem tam giác ABC với AB < AC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho AM = EM.
a. Chứng minh rằng ΔAMB bằng ΔMCE
b. Từ điểm A, vẽ đường thẳng AH vuông góc với BC. Trên tia đối của tia HA, chọn điểm D sao cho HA = HD. Chứng minh rằng CE = BD
c. Tam giác AMD thuộc loại tam giác gì? Giải thích lý do.
Đáp án cho bài kiểm tra giữa kỳ 2 môn Toán lớp 7
I. Phần Trắc Nghiệm
Câu 1: Đáp án C
Câu 2: Lựa chọn A
Câu 3: Lựa chọn A
Câu 4: Lựa chọn B
Câu 5: Lựa chọn C
Câu 6: Lựa chọn D
Câu 7: Đáp án D
Câu 8: Đáp án D
II. Phần tự luận
Bài 1:
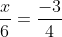
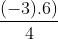
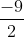
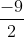
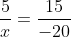
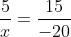
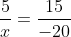
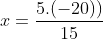
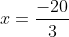
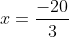

3(x + 11) = 2(14 - x)
3x + 33 = 28 - 2x
3x + 2x = 28 - 33
5x = -5
x = -1
Do đó, x = -1
Bài 2
a) Chúng ta có: 2a = 5b
=> a/5 = b/2
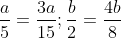

=> 3a = 2 \times 15 = 30 => a = 10
ab = 2 \times 8 = 16 => b = 4
b) Tỉ lệ a : b : c = 2 : 4 : 5

=> a = 2 \times 3 = 6
b = 4 \times 3 = 12
c = 5 \times 3 = 15
Bài 3:
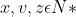
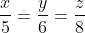
Số sách lớp 7C nhiều hơn lớp 7A là 24 quyển, do đó z - x = 24
Áp dụng quy tắc của dãy tỉ lệ bằng nhau, ta có:
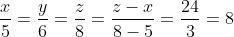
=> x = 5 \times 8 = 40; y = 6 \times 8 = 48; z = 8 \times 8 = 64
Số sách các lớp 7A, 7B, và 7C quyên góp lần lượt là 40 quyển, 48 quyển, và 64 quyển.
Bài 4
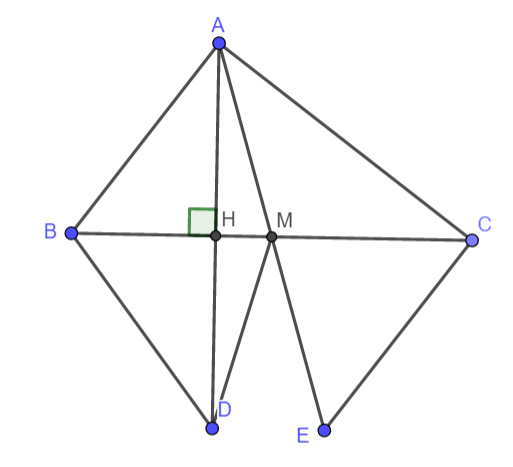
a. Xem xét tam giác ABM và tam giác MEC, ta có:
BM = MC (M là trung điểm của đoạn BC)
Góc AMB bằng góc CME (góc đối đỉnh), và AM = ME (theo giả thiết), do đó ΔAMB bằng ΔMCE (cạnh-góc-cạnh).
b. Xem xét tam giác ABH vuông tại H và tam giác BHD vuông tại H, ta có:
BH là cạnh chung, AH = DH (theo giả thiết), dẫn đến ΔABH bằng ΔBDH, nên AB = BD (1).
Từ ΔAMB = ΔMCE (đã chứng minh), ta suy ra AB = CE (2). Kết hợp (1) và (2), ta có CE = BD.
c. Từ kết quả ở câu b, ta dễ dàng nhận thấy rằng MA = MD.
Do đó, tam giác AMD là tam giác cân tại đỉnh M.
2. Đề kiểm tra giữa kỳ 2 môn Toán lớp 7
I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Vui lòng chọn phương án đúng duy nhất cho mỗi câu hỏi dưới đây.
Câu 1. Cho tỉ lệ 5/125 = x/-100. Điền số vào ô trống để tỉ lệ thức đúng là
A. 4; B. −4; C. 2; D. 8.
Câu 2. Đối với hai đại lượng c và d liên kết bởi công thức c = 25d, phát biểu nào sau đây là chính xác?
A. c tỉ lệ thuận với d với hệ số tỉ lệ là –25;
B. c tỉ lệ thuận với d với hệ số tỉ lệ là 1/25;
C. d tỉ lệ thuận với c với hệ số tỉ lệ là 1/25;
D. d tỉ lệ nghịch với c với hệ số tỉ lệ là 25.
Câu 3. Nếu x và y tỉ lệ nghịch với nhau, và khi x = 2 thì y = 5, thì hệ số tỉ lệ nghịch a giữa x và y là bao nhiêu?
A. 10; B. 2/5; C. –10; D. 5/2.
Câu 4. Xem hình dưới đây:
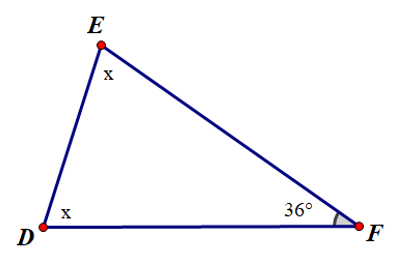
Giá trị của x là:
A. 18 độ
B. 72 độ
C. 36 độ
D. Không thể xác định
Câu 5. Hai tam giác được coi là bằng nhau khi:
A. Hai tam giác có ba cặp cạnh tương ứng đồng thời bằng nhau;
B. Hai tam giác có ba cặp góc tương ứng đồng thời bằng nhau;
C. Hai tam giác có ba cặp cạnh và ba cặp góc tương ứng bằng nhau;
D. Hai tam giác có hai cạnh tương ứng bằng nhau.
Câu 6. Trong một tam giác cân với góc đáy là 40 độ, góc ở đỉnh có số đo là bao nhiêu?
A. 50 độ
B. 40 độ
C. 140 độ
D. 100 độ
Câu 7. Trong tam giác MNP với MN < MP và MD ⊥ NP, khẳng định nào sau đây là chính xác?
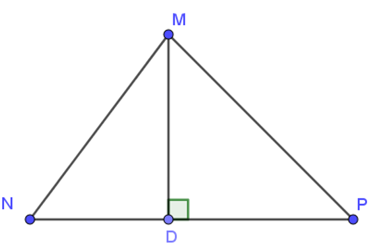
A. DN = DP
B. MN = MP
C. MD > MN
D. MD < MP
Câu 8. Điền vào chỗ trống: “Điểm … hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó”
A. thuộc; B. cách đều; C. nằm trên; D. nằm trong.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. Ba lớp 7 cùng được giao trồng tổng cộng 36 cây. Lớp 7A trồng được 1/5 số cây, lớp 7B trồng 1/3 số cây, và lớp 7C trồng 3/7 số cây. Số cây còn lại của mỗi lớp là như nhau. Tính số cây mỗi lớp đã trồng được.
Bài 2. Cho góc bẹt xOy với tia phân giác Ot. Trên tia Ot, chọn hai điểm A và B sao cho A nằm giữa O và B. Chọn điểm C trên tia Ox sao cho OC = OB, và điểm D trên tia Oy sao cho
a) Chứng minh rằng AC = BD và AC ⊥ BD.
b) Gọi M và N lần lượt là trung điểm của AC và BD. Chứng minh rằng OM = ON.
c) Tính các góc của tam giác MON.
d) Chứng minh rằng AD ⊥ BC.
Bài 3: Ban đầu, một công việc được giao cho 3 người làm trong 12 ngày. Tuy nhiên, chỉ có 2 người thực hiện và họ phải làm thêm mỗi ngày 1 giờ để hoàn thành công việc trong 16 ngày. Biết rằng năng suất lao động của họ là giống nhau, hãy tính số giờ làm việc mỗi ngày của họ.
