1. Đề thi học kì 2 môn Toán lớp 7 (theo sách Cánh Diều - Đề số 1)
Phòng Giáo dục và Đào tạo ...
Trường THCS ...
Đề thi học kì 2 - Cánh Diều
Năm học 2022 - 2023
Môn: Toán lớp 7
Thời gian làm bài: 90 phút (không bao gồm thời gian phát đề)
Phần I. Trắc nghiệm khách quan (3 điểm)
Vui lòng chọn đáp án đúng duy nhất cho từng câu hỏi dưới đây bằng cách khoanh tròn.
Câu 1: Các dãy dữ liệu được cho như sau:
(1) Danh sách tên của từng học sinh lớp 7A.
(2) Số lượng học sinh đạt điểm 10 trong kỳ thi giữa học kỳ I của các lớp 7.
(3) Số nhà của từng học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của từng học sinh trong lớp.
Trong các dãy dữ liệu đã nêu, dãy dữ liệu nào không phải là số?
A. (1)
B. (2)
C. (3)
D. (4)
Câu 2. Biểu thức đại số nào diễn tả bình phương của tổng hai số a và b?
A. a² − b²
B. a² + b²
C. (a − b)²
D. (a + b)²
Câu 3. Tính giá trị của biểu thức x³ − 2x² khi x = −2.
A. −16
B. 16
C. 0
D. −8
Câu 4: Một người đi bộ trong x giờ với tốc độ 4 km/h và sau đó di chuyển bằng xe đạp trong y giờ với tốc độ 18 km/h. Biểu thức đại số nào diễn tả tổng quãng đường đã đi của người đó?
A. 4(x + y)
B. 22(x + y)
C. 4y + 18x
D. 4x + 18y
Câu 5: Hệ số tự do của đa thức 10 − 9x² − 7x⁵ + x⁶ − x⁴ là gì?
A. −1
B. −7
C. 1
D. 10
Câu 6: Sắp xếp các hạng tử của đa thức P(x) = 2x³ − 7x² + x⁴ − 4 theo thứ tự giảm dần của lũy thừa biến sẽ được:
A. P(x) = x⁴ + 2x³ − 7x² − 4
B. P(x) = 7x² + 2x³ + x⁴ − 4
C. P(x) = −4 − 7x² + 2x³ + x⁴
D. P(x) = x⁴ − 2x³ − 7x² − 4
Câu 7: Trong tam giác MNP với NP = 1 cm và MP = 7 cm, độ dài cạnh MN là một số nguyên (cm). Độ dài của cạnh MN là:
A. 8 cm
B. 5 cm
C. 6 cm
D. 7 cm
Câu 8: Đội múa có 1 bạn nam và 5 bạn nữ. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều có khả năng được chọn. Tính xác suất của biến cố “Bạn được chọn là nam”.
A. 1
B. 1/5
C. 5/6
D. 1/6
Câu 9: Điểm giao nhau của ba đường trung trực trong tam giác là:
A. cách đều ba cạnh của tam giác.
B. được gọi là tâm đường tròn ngoại tiếp của tam giác.
C. cách đều ba đỉnh của tam giác.
D. cách đỉnh một đoạn bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
Câu 10: Trong một tam giác, đối diện với cạnh nhỏ nhất là một
A. góc nhọn
B. góc vuông
C. góc tù
D. Góc bẹt
Câu 11: Trong các bộ ba số dưới đây, bộ nào có thể là ba cạnh của một tam giác?
A. 7 cm, 3 cm, 4 cm
B. 7 cm, 3 cm, 5 cm
C. 7 cm, 3 cm, 2 cm
D. 7 cm, 3 cm, 3 cm
Câu 12: Trong tam giác ABC với ∠A = 90° và ∠C = 30°, mối quan hệ giữa ba cạnh AB, AC và BC là:
A. BC > AB > AC
B. AC > AB > BC
C. AB > AC > BC
D. BC > AC > AB
Phần II. Bài tập tự luận (7.0 điểm)
Câu 1: Xét hai đa thức sau: f(x) = x^5 + x^3 - 4x - x^5 + 3x + 7 và g(x) = 3x^2 - x^3 + 8x - 3x^2 - 14.
a) Đơn giản hóa và sắp xếp hai đa thức f(x) và g(x) theo thứ tự giảm dần của các lũy thừa.
b) Tính tổng f(x) + g(x) và xác định các nghiệm của đa thức này.
Câu 2: Xét tam giác ABC cân tại đỉnh A, vẽ đường AH vuông góc với BC (H thuộc BC). Gọi P là trung điểm của HC. Trên tia đối của tia PA, chọn điểm Q sao cho QP = PA.
a) Chứng minh rằng: ΔAPH = ΔQPC và QC vuông góc với BC.
b) Chứng minh rằng: QC = AH, từ đó suy ra AC > QC.
c) Chứng minh rằng: ∠PAC < ∠HAP.
d) Gọi I là trung điểm của BQ. Chứng minh rằng ba điểm A, H, I nằm trên một đường thẳng.
Câu 3: Xét đa thức f(x) = ax³ + bx² + cx + d với a là số nguyên dương và biết rằng f(5) - f(4) = 2019. Chứng minh rằng f(7) - f(2) là một số hợp.
2. Đáp án Đề thi cuối kỳ 2 Toán 7 sách CÁNH DIỀU
Phần I. Trắc nghiệm khách quan (3.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Đáp án | A | D | A | D | D | A | D | D | C | A | B | D |
Phần II. Tự luận (7.0 điểm)
Câu 1:
a) f(x) = x⁵ + x³ − 4x − x⁵ + 3x + 7
f(x) = (x⁵ − x⁵) + x³ + (−4x + 3x) + 7
f(x) = x³ − x + 7
g(x) = 3x² − x³ + 8x − 3x² − 14
g(x) = −x³ + (3x² − 3x²) + 8x − 14
g(x) = −x³ + 8x − 14
b) f(x) + g(x) = x³ − x + 7 − x³ + 8x − 14 = (x³ − x³) + (−x + 8x) + (7 − 14) = 7x − 7
Do đó, f(x) + g(x) = 7x − 7
7x − 7 = 0
7x = 7
x = 1
Nên x = 1 là nghiệm của đa thức f(x) + g(x).
Câu 2:
a. Xét hai tam giác Δ APH và Δ QPC có:
+ HP = PC (đã cho)
+ ∠ APH = ∠ QPC (đối đỉnh)
+ QP = PA (đã cho)
⇒ Δ APH ≅ Δ QPC (c.g.c) (đã chứng minh)
⇒ ∠ AHP = ∠ QCP = 90° (hai góc tương ứng)
⇒ QC ⊥ BC (đã chứng minh).
b. Theo (a), Δ APH ≅ Δ QPC ⇒ QC = AH (hai cạnh tương ứng) (1)
Mà Δ AHC vuông tại H
⇒ AH < AC (cạnh góc vuông < cạnh huyền) (2)
Từ (1) và (2), suy ra QC < AC (đã chứng minh).
c. Xét Δ AQC có QC < AC ⇒ ∠ QAC < ∠ AQC (3) (Mối quan hệ giữa cạnh và góc trong tam giác)
Mặt khác, Δ APH ≅ Δ QPC ⇒ ∠ HAP = ∠ PQC = ∠ AQC (4)
Từ (3) và (4) ⇒ ∠ HAP < ∠ QAC hay ∠ HAP < ∠ PAC (đã chứng minh).
d. Xét Δ ABQ có BP là trung tuyến ứng với cạnh AQ
Mà BH = 2HP (do H là trung điểm của BC, P là trung điểm của HC)
⇒ H là trọng tâm Δ ABQ (5)
Còn I là trung điểm của BQ ⇒ AI là trung tuyến ứng với cạnh BQ (6)
Từ (5) và (6) ⇒ H thuộc đường thẳng AI ⇒ A, H, I thẳng hàng (đã chứng minh).
Câu 3:
Ta có:
f(5) = 125a + 25b + 5c + d
f(4) = 64a + 16b + 4c + d
⇒ f(5) - f(4) = 61a + 9b + c = 2019
Cũng có:
f(7) = 343a + 49b + 7c + d
f(2) = 8a + 4b + 2c + d
⇒ f(7) - f(2)
= 335a + 45b + 5c
= 5 × (67a + 9b + c)
= 5 × 1019
Vậy f(7) - f(2) là hợp số. (đã chứng minh).
3. Đề thi học kỳ 2 môn Toán lớp 7 (Sách Cánh Diều - Đề số 2)
Phòng Giáo dục và Đào tạo ...
Trường THCS ...
Đề thi Học kỳ 2 - Cánh Diều
Năm học 2022 - 2023
Môn: Toán lớp 7
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
Phần I. Trắc nghiệm khách quan (3.0 điểm)
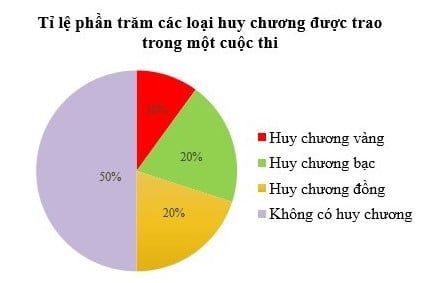
Xác định đối tượng có tỷ lệ phần trăm cao nhất:
A. Huy chương vàng;
B. Huy chương bạc;
C. Huy chương đồng;
D. Không có huy chương.
Câu 9: Tam giác ABC có đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài của GM?
A. GM = 6 cm;
B. GM = 9 cm;
C. GM = 3 cm;
D. GM = 18 cm.
Câu 10: Hình hộp chữ nhật có tổng cộng bao nhiêu cạnh?
A. 4
B. 6
C. 8
D. 12
Câu 11: Hai đại lượng x và y tỷ lệ nghịch với nhau, biết rằng khi x = –12 thì y = 8. Khi x = 3 thì y sẽ bằng:
A. –32;
B. 32;
C. –2;
D. 2.
Câu 12: Trong các tuyên bố dưới đây, tuyên bố nào là không chính xác?
A. Hình lăng trụ đứng tam giác có 4 mặt, 6 đỉnh
B. Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh
C. Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác và tam giác là Sxq = C.h
D. Hình lăng trụ đứng tứ giác có các mặt bên là các hình chữ nhật
Phần II. Tự luận (7.0 điểm)
Câu 1: Tính chu vi của hình chữ nhật khi chiều dài và chiều rộng của nó có tỷ lệ lần lượt là 5:3 và chiều dài lớn hơn ba lần chiều rộng là 8 cm.
Câu 2: Cho hai đa thức P(x) = x^5 + 2x^3 - 4x^3 + x^2 + 4x + 9 và Q(x) = x^5 + 9 + 2x^2 - 4x^2 - 2x^3 + 3x. Hãy thực hiện các bước sau: a) Rút gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến. b) Tính giá trị của P(x) - Q(x).
Câu 3: Trong tam giác ABC cân tại A, trên cạnh AB, chọn điểm M và trên tia đối của tia CA, chọn điểm N sao cho AM + AN = 2AB. a) Chứng minh rằng BM = CN. b) Chứng minh rằng BC đi qua trung điểm của đoạn thẳng MN. c) Đường trung trực của MN và tia phân giác của góc BAC cắt nhau tại điểm K. Chứng minh rằng tam giác BKM bằng tam giác CKN và từ đó suy ra KC vuông góc với AN.
4. Đáp án Đề thi cuối kỳ 2 Toán lớp 7 theo sách CÁNH DIỀU
Phần I. Trắc nghiệm (3.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Đáp án | B | A | A | D | C | A | D | D | C | D | A | A |
Phần II. Bài tập tự luận (7.0 điểm)
Câu 1: Cho hình chữ nhật với chiều dài x và chiều rộng y (cm), với x và y > 0. Theo đề bài, chiều dài và chiều rộng của hình chữ nhật tỉ lệ với 5 và 3, do đó x/5 = y/3. Hơn nữa, hai lần chiều dài nhiều hơn ba lần chiều rộng là 8 cm, nghĩa là 2x - 3y = 8. Áp dụng tính chất dãy tỉ số bằng nhau, ta có: x/5 = y/3 = 8. Từ đó x = 40 và y = 24. Chu vi hình chữ nhật là 2(x + y) = 2(40 + 24) = 128 cm.
Câu 2: a) Rút gọn và sắp xếp theo lũy thừa giảm dần của biến. Đối với F(x): F(x) = 5x^2 - 1 + 3x + x^2 - 5x^3. Rút gọn: F(x) = -5x^3 + 6x^2 + 3x - 1. Đối với G(x): G(x) = 2 - 3x^3 + 6x^2 + 5x - 2x^3 - x. Rút gọn: G(x) = -5x^3 + 6x^2 + 4x + 2. b) Tính M(x): M(x) = F(x) - G(x) = (-5x^3 + 6x^2 + 3x - 1) - (-5x^3 + 6x^2 + 4x + 2). Tính ra M(x) = -x - 3. Nghiệm của M(x) là x = -3.
Câu 3: a) Trong tam giác ABC cân tại A, ta có AB = AC. Vì AM + AN = 2AB nên BM = CN. b) Gọi I là giao điểm của MN và BC. Từ BM = CN, ME // NC, ta chứng minh rằng I là trung điểm của MN. c) Xét hai tam giác MIK và NIK, với MI = NI và các góc vuông. Từ đó ΔMIK = ΔNIK, suy ra KM = KN. Tiếp theo, chứng minh ΔABK = ΔACK và ΔBKM = ΔCKN, từ đó suy ra KC vuông góc với AN.
Câu 4: Đáp án Đề thi cuối kỳ 2 môn Toán lớp 7 theo sách CÁNH DIỀU.
