Đề thi học kỳ 2 môn Toán lớp 7 với đáp án chi tiết

1. Đề thi học kỳ 2 môn Toán lớp 7

Đề thi học kỳ 2 môn Toán lớp 7

PHÒNG GD&ĐT.......

TRƯỜNG THCS...........

ĐỀ THI HỌC KỲ 2 NĂM HỌC 2022 - 2023

MÔN: TOÁN 7 Theo sách KNTTVCS

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm) Chọn phương án đúng duy nhất cho mỗi câu hỏi dưới đây:

Câu 1. Từ đẳng thức 2.15 = 6.5, lập được tỉ lệ thức nào dưới đây?

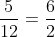
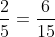
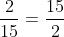
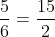
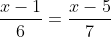
A. x = –27; B. x = –23; C. x = 23; D. x = 27.

Câu 3. Đại lượng y tỉ lệ nghịch với đại lượng x nếu:

A. x = ay với a là hằng số khác 0;

C. y = ax với a là hằng số khác 0;

Câu 4. Trong số các biểu thức dưới đây, biểu thức nào là biểu thức số?

A. 32 − 4;

B. x – 6 + y;

C. x^2 + x;

Câu 5. Xét hai biểu thức: E = 2(a + b) – 4a + 3 và F = 5b – (a – b). Khi a = 5 và b = –1, chọn khẳng định đúng:

A. E = F;

B. E > F;

C. E < F;

D. E ≈ F.

Câu 6. Giá trị x = ‒1 là nghiệm của đa thức nào dưới đây?

A. M(x) = x – 1;

B. N(x) = x + 1;

C. P(x) = x;

D. Q(x) = –x.

Câu 7. Trong một phép thử, bạn An biết được xác suất của biến cố M là 1/3 và của biến cố N là 1/2. Vậy biến cố nào có khả năng xảy ra thấp hơn?

A. Biến cố M;

B. Biến cố N;

C. Cả hai biến cố M và N đều có khả năng xảy ra như nhau;

D. Không thể xác định.

Câu 8. Khẳng định nào sau đây là chính xác?

A. Trong một tam giác, cạnh đối diện với góc lớn hơn luôn là cạnh dài hơn;

B. Trong một tam giác, góc đối diện với cạnh ngắn hơn là góc lớn hơn;

C. Trong một tam giác vuông, cạnh huyền không phải là cạnh ngắn nhất;

D. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh dài nhất.

Câu 9. Cho ∆ABC với AB > BC > AC. Chọn khẳng định không đúng:

A. AB < BC – AC;

B. AB > BC – AC;

C. AC > AB – BC;

D. AC < AB + BC.

Câu 10. Trong tam giác ABC, nếu ba đường trung trực của tam giác đi qua một điểm M, khẳng định nào dưới đây là chính xác?

A. M cách đều ba đỉnh của tam giác ABC;

B. M cách đều ba cạnh của tam giác ABC;

C. M là trọng tâm của tam giác ABC;

D. M là trực tâm của tam giác ABC.

Câu 11. Đặc điểm nào dưới đây không giống nhau giữa hình hộp chữ nhật và hình lập phương?

A. Tất cả các cạnh đều bằng nhau;

B. Các mặt đáy đều song song;

C. Các cạnh bên đều song song với nhau;

D. Có tổng cộng 8 đỉnh.

Câu 12. Một hình hộp chữ nhật có diện tích xung quanh là 180 cm², với chiều dài hai cạnh đáy lần lượt là 8 cm và 10 cm. Tính chiều cao của hình hộp chữ nhật.

A. 2 cm; B. 4 cm; C. 5 cm; D. 10 cm.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (2,0 điểm) Cho đa thức A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Đơn giản hóa và sắp xếp đa thức A(x) theo thứ tự giảm dần của các số mũ, sau đó xác định bậc và hệ số cao nhất của đa thức.

b) Xác định đa thức M(x) sao cho M(x) = A(x) * B(x), với B(x) = x – 1.

c) Tìm các nghiệm của đa thức A(x).

Bài 2. (1,0 điểm) Ba nhóm công nhân cùng làm việc để chuyển một khối lượng gạch như nhau. Thời gian để nhóm thứ nhất, nhóm thứ hai và nhóm thứ ba hoàn thành công việc lần lượt là 2 giờ, 3 giờ và 4 giờ. Xác định số lượng công nhân trong mỗi nhóm, biết rằng nhóm thứ ba có ít hơn nhóm thứ hai 5 công nhân và năng suất lao động của các công nhân là đồng nhất.

Bài 3. (1,0 điểm) Chọn ngẫu nhiên một số từ tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Xác định biến cố nào là biến cố chắc chắn, biến cố không thể xảy ra và biến cố ngẫu nhiên trong số các biến cố sau đây:

A: “Số được chọn là số nguyên tố”; B: “Số được chọn là số có một chữ số”; C: “Số được chọn là số tròn chục”.

b) Tính xác suất của biến cố A.

Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A, với đường phân giác BD (D∈AC). Kẻ từ D một đường DH vuông góc với BC.

a) Chứng minh rằng ΔABD và ΔHBD là hai tam giác vuông đồng dạng.

b) So sánh độ dài của AD và DC.

c) Gọi K là điểm chung của đường thẳng AB và DH, I là trung điểm của đoạn KC. Chứng minh rằng ba điểm B, D, I nằm trên cùng một đường thẳng.

2. Đáp án cho đề thi học kỳ 2 môn Toán lớp 7

PHẦN I. Trắc nghiệm (3,0 điểm)

II. Tự luận Bài 1. (2,0 điểm)

a) Xét đa thức: A(x) = –11x^5 + 4x – 12x^2 + 11x^5 + 13x^2 – 7x + 2

= x^2 – 3x + 2.

Đa thức A(x) có bậc bằng 2 và hệ số của bậc cao nhất là 1.

b) Tính đa thức M(x) = A(x) × B(x)

= (x^2 – 3x + 2) × (x – 1)

= x × (x^2 – 3x + 2) – 1 × (x^2 – 3x + 2)

= x^3 – 3x^2 + 2x – x^2 + 3x – 2

= x^3 – 4x^2 + 5x – 2

= x^2 – 4x + 2

= x^2 – x – 2

= 0 × (x – 1) – 2 × (x – 1)

= 0 × (x – 1)(x – 2) = 0

x = 1 hoặc x = 2.

Vậy, đa thức A(x) có các nghiệm x thuộc {1, 2}.

Bài 2. (1,0 điểm)

Đặt số công nhân của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là x, y và z.

Đội ba có ít công nhân hơn đội hai 5 người, do đó y – z = 5.

Với khối lượng công việc không đổi, số công nhân và thời gian hoàn thành công việc của các đội có mối quan hệ tỷ lệ nghịch.

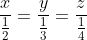
Áp dụng quy tắc tỉ số bằng nhau, ta có:

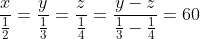
Từ đó, ta tính được x = 60 \times \frac{1}{2} = 30, y = 60 \times \frac{1}{3} = 20, z = 60 \times \frac{1}{4} = 15.

Do đó, số công nhân của đội thứ nhất, đội thứ hai và đội thứ ba lần lượt là 30, 20 và 15 người.

Bài 3. (1,0 điểm) Xét tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Tập hợp M bao gồm cả số nguyên tố và số hợp số, vì vậy biến cố A thuộc loại biến cố ngẫu nhiên.

Trong tập hợp M, mọi số đều là số có một chữ số, vì vậy biến cố B là biến cố chắc chắn. Đồng thời, vì tập hợp M không chứa số nào là số tròn chục, nên biến cố C là biến cố không thể xảy ra.

b) Tập hợp M có tổng cộng 6 số, trong đó có 3 số nguyên tố là 2, 3 và 5.

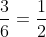
Bài 4. (2,5 điểm)

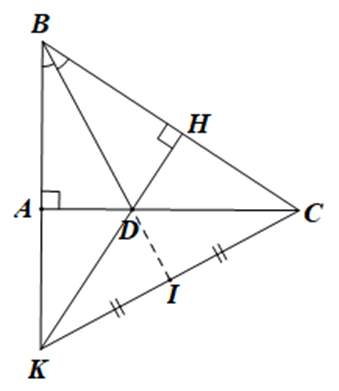
Do đó, tam giác ΔABD đồng dạng với tam giác ΔHBD vì cạnh huyền và góc nhọn tương ứng.

b) Từ việc ΔABD đồng dạng với ΔHBD, ta suy ra AD = HD vì hai cạnh tương ứng. Xét tam giác ΔDHC vuông tại H, với DC là cạnh huyền, chứng tỏ DC lớn hơn HD và AD.

c) Xét tam giác ΔBKC với CA ⊥ BK, KH ⊥ BC, và CA cắt KH tại D. Do đó, D là trực tâm của ΔBKC, và BD ⊥ KC (1).

Vì vậy, tam giác ΔBKJ đồng dạng với ΔBCJ (cạnh góc vuông và góc nhọn kề), từ đó KJ = CJ (hai cạnh tương ứng).

Do đó, J là trung điểm của KC. Vì I cũng là trung điểm của KC nên I và J trùng nhau, do đó ba điểm B, D, I nằm trên một đường thẳng.

Bài 5. (0,5 điểm) Tiến hành chia đa thức 2n² – n + 2 cho đa thức 2n + 1 như sau:

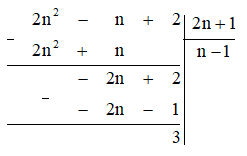
Để đảm bảo rằng 2n² – n + 2 chia hết cho 2n + 1, ta cần kiểm tra các giá trị của (2n + 1) thuộc tập Ư(3) = {1; ‒1; 3; ‒3}. Dưới đây là bảng kết quả:

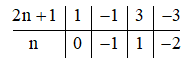
Do đó, n có thể nhận các giá trị thuộc tập {–2; –1; 0; 1}.