Đề thi Toán lớp 10 cho học kỳ 1 của các chương trình Kết nối tri thức, Cánh diều, và Chân trời sáng tạo

Buzz

Nội dung bài viết

1. Đề thi môn Toán lớp 10 học kỳ 1 theo chương trình Kết nối tri thức

2. Đề thi học kỳ 1 lớp 10 môn Toán chân trời sáng tạo

3. Đề kiểm tra toán lớp 10 học kỳ 1 của sách Cánh Diều

Xem thêm

Dưới đây, Mytour cung cấp thông tin chi tiết về đề thi Toán lớp 10 học kỳ 1 cho các chương trình Kết nối tri thức, Cánh diều, và Chân trời sáng tạo. Mong rằng bài viết này sẽ hữu ích cho bạn đọc.

1. Đề thi môn Toán lớp 10 học kỳ 1 theo chương trình Kết nối tri thức

I. Phần trắc nghiệm (7 điểm)

Câu 1: Trong các câu dưới đây, câu nào không phải là một mệnh đề?

A. 2 là một số nguyên âm

B. Bạn có yêu thích môn Toán không?

C. 13 là một số nguyên tố

D. Số 15 không chia hết cho 2

Câu 2: Trong các tập hợp dưới đây, tập hợp nào là tập con của A = { 1; 2; 3; 4; 5 }?

A. A1 = { 1; 6 }

B. A2 = { 0; 1; 3 }

C. A3 = { 4; 5 }

D. A4 = { 0 }

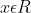
A. ( -5 ; 1 )

B. ( -5 ; 3 )

C. ( -3 ; 1 )

D. ( -3 ; 3 )

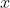
A. ( 0 ; 0 )

B. ( 1 ; 1 )

C. ( -1 ; 1 )

D. ( -1 ; -1 )

Câu 5: Mệnh đề nào dưới đây là chính xác?

A. sin ( 180° - a) = -sin a

B. cos ( 180° - a) = -cos a

C. tan ( 180° - a) = -tan a

D. cot ( 180° - a) = -cot a

Câu 6. Trong tam giác ABC với BC = 1, AC = 3 và góc C là 60 độ, tính độ dài của cạnh AB

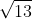
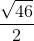
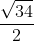
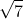
Câu 7: Cho lục giác đều ABCDEF với tâm O như hình vẽ. Vectơ OB có cùng phương với vectơ nào dưới đây?

A. Vectơ OC

B. Vectơ BC

C. Vectơ BE

D. Vectơ OA

Câu 8: Mệnh đề nào dưới đây là sai?

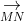
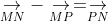
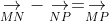
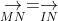
$\underset{MN}{\rightarrow} + \underset{NP}{\rightarrow} = \underset{MP}{\rightarrow}$ $\underset{MN}{\rightarrow} - \underset{MP}{\rightarrow} = \underset{PN}{\rightarrow}$ $\underset{MN}{\rightarrow} - \underset{NP}{\rightarrow} = \underset{MP}{\rightarrow}$ $\underset{MN}{\rightarrow} = \underset{IN}{\rightarrow} + \underset{MI}{\rightarrow}$

Câu 9: Cho hình chữ nhật ABCD với AB = 4 cm, AD = 3 cm. Tính giá trị của |BC + BA|

A. 5 cm

B. 7 cm

C. 9 cm

D. 11 cm

Câu 10: Cho G là trung điểm của tam giác ABC và M là một điểm bất kỳ. Đẳng thức nào dưới đây là đúng?

A. MA + MB + MC = MG

B. MA + MB + MC = 2MG

C. MA + MB + MC = 3MG

D. MA + MB + MC = 4MG

Câu 11: Xét ba điểm A, B, C. Đẳng thức nào dưới đây là chính xác?

A. MB = 3 MA

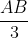
$B. \frac{AB}{3}$

C. AB = 4 MA

D. MB = -3 MA

Câu 12: Trong mặt phẳng tọa độ Oxy, với u = 2i + j. Xác định tọa độ của u.

A. u (2; -1)

B. u (-2; 1)

C. u (2; 1)

D. u (-2; -1)

Câu 13: Trong mặt phẳng tọa độ, vecto nào dưới đây có cùng phương?

A. vecto a = (1; 0) và vecto b = (0; 1)

B. vecto u = (3; -2) và vecto v = (6; 4)

C. vecto i = (2; 3) và vecto j = (-6; -9)

D. vecto c = (2; 3) và vecto d = (-6; 9)

Câu 14: Cho hình thoi ABCD. Vecto không có điểm đầu là A, vậy điểm cuối của vecto đó là:

A. Điểm kết thúc là điểm A

B. Điểm kết thúc là điểm B

C. Điểm kết thúc là điểm C

D. Điểm kết thúc là điểm D

Câu 15: Cho tam giác ABC với các cạnh AB = 3, BC = 4 và AC = 5. Tính giá trị của BA . BC

A. 1

B. 0

C. 12

D. 20

Câu 16: Một lực F có cường độ 60N tác động vào điểm M, làm cho vật di chuyển theo hướng nằm ngang từ N đến M với quãng đường 10m. Biết góc giữa lực F và phương thẳng đứng là 30 độ, tính công do lực F sinh ra.

A. 900 J

B. 800 J

C. 600 J

D. 300 J

Câu 17: Tính giá trị trung bình của tập hợp số liệu sau: 2, 5, 8, 7, 10, 20, 11

A. 8

B. 9

C. 10

D. 11

Câu 18: Xác định trung vị của tập dữ liệu sau: 0, 1, 2, 3, 5, 9, 10

A. 3

B. 5

C. 0

D. 2

Câu 19: Xem xét tập số liệu sau: 5, 2, 9, 10, 15, 5, 20

Tứ phân vị Q1, Q2, Q3 của tập số liệu trên lần lượt là:

A. 2; 5; 9

B. 5; 9; 15

C. 10; 5; 15

D. 2; 9; 15

Câu 20: Xem xét tập số liệu sau: 12; 5; 8; 11; 6; 20; 22

Tính giá trị khoảng biến thiên của tập số liệu này

A. 16

B. 17

C. 18

D. 19

Câu 21: Trong hệ tọa độ Oxy, cho ba điểm A(2; 1), B(1; 10) và C (m ; 2m - 17). Xác định tất cả các giá trị của tham số m để AB vuông góc với OC.

A. m = 9

B. m = -9

D. m = 1

D. m = -1

Câu 22. Xem xét tập số liệu sau: 10; 3; 6; 9; 15. Tính độ lệch chuẩn của tập số liệu này (làm tròn đến hai chữ số thập phân)

A. 3,03

B. 4,03

C. 5,03

D. 6,03

II. Tự luận

Bài 1: Từ hai điểm quan sát A và B của một tòa nhà, người ta nhìn thấy đỉnh C của ngọn núi. Biết rằng khoảng cách AB = 70, góc giữa phương nhìn AC và phương ngang là 30 độ, còn góc giữa phương nhìn BC và phương ngang là 15 độ 30 phút. Tính độ cao của ngọn núi so với mặt đất (làm tròn đến hai chữ số thập phân)

Bài 2: Cho tam giác đều ABC với cạnh dài a. Trên các cạnh BC, CA, AB lần lượt chọn các điểm N, M, P sao cho BN = a / 3, CM = 2a / 3, và AP = x (0 < x < a). Xác định giá trị của x theo a để đường thẳng AN vuông góc với đường thẳng PM.

Đáp án:

I. Kiểm tra kiến thức

1. D	2. B	3. D	4. A	5. B	6. D	7. B	8. C	9. C	10. C	11. C
12. B	13. C	14. C	15. A	16. B	17. C	18. B	19. C	20. A	21. B	22. A

II. Phần tự luận

Bài 1: 13km

Bài 2: x = 5

2. Đề thi học kỳ 1 lớp 10 môn Toán chân trời sáng tạo

I. Đánh giá kiến thức

Câu 1: Trong số các câu sau, câu nào là một mệnh đề?

A. Có ai trong đó không?

B. Bạn có cảm thấy đói không?

C. Đừng lại gần tôi!

D. Số 25 không phải là số nguyên tố

Câu 2: Trong hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Cho biết: CD = 8cm; MN = 6cm. Tìm độ dài của đoạn AB.

A. 2cm B. 4cm C. 6cm D. 8cm

Câu 3: Khẳng định nào sau đây là chính xác?

A) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.

B) Hình bình hành với hai đường chéo bằng nhau là hình chữ nhật

C) Hình thang có một góc vuông là hình chữ nhật

D) Hình thang cân với hai đường chéo bằng nhau là hình chữ nhật.

Câu 4: Hình nào dưới đây luôn có tâm đối xứng?

A) Hình thang B) Hình thang cân

C) Hình bình hành D) Đáp án đúng là A, B, C

Câu 5: Khẳng định nào dưới đây là chính xác?

A) Hình bình hành có một góc vuông sẽ là hình thoi.

B) Tứ giác có hai cặp cạnh đối song song là hình bình hành.

C) Hình thang có một góc vuông sẽ là hình chữ nhật.

D) Hình thoi với một góc 60° không trở thành hình chữ nhật.

Câu 6: Trong tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Tính diện tích S của tam giác ABC nếu diện tích tam giác MNP là 4 (đvdt).

A. S = 12 (đvdt) B. S = 15 (đvdt)

C. S = 20 (đvdt) D. S = 16 (đvdt)

II. Phần tự luận

Câu 1: Xét hình chữ nhật MNPQ. Gọi A là điểm hạ từ P vuông góc đến NQ. Gọi B, C, D lần lượt là trung điểm của PA, AQ, MN.

a) Chứng minh rằng: BC // MN

b) Chứng minh rằng tứ giác CDNB là hình bình hành

c) Gọi E là điểm giao của NB và PC, F là chân đường vuông góc từ D đến NB. Chứng minh rằng tứ giác FDCE là hình chữ nhật

d) Hạ đường thẳng CG vuông góc với MN tại G; BC cắt NP tại H, chứng minh rằng DB cắt GH tại trung điểm của mỗi đoạn đường.

Câu 2: Xét tam giác ABC với ba góc nhọn và AB nhỏ hơn AC. Hai đường cao BE và CF giao nhau tại điểm H. Gọi M là trung điểm của BC. Trên tia đối của MH, lấy điểm K sao cho HM = MK.

a) Chứng minh rằng tứ giác BHCK là hình bình hành.

b) Xét điểm I là điểm đối xứng của H qua BC. Chứng minh rằng tứ giác BIKC là hình thang cân.

Đáp án:

I. Trắc nghiệm

1. A

2. B

3. C

4. B

5. A

6. A

II. Tự luận

Câu 1: Hướng dẫn giải bài toán:

a. Chứng minh rằng MNPQ là hình chữ nhật, tức là MN song song với PQ và BC song song với MN.

b. Chứng minh rằng BC là đường trung bình của tam giác APQ, nên BC song song với DN và CDNB là hình bình hành.

c. Chứng minh rằng BC song song với PQ, nên NB vuông góc với CP; FE vuông góc với CE, từ đó suy ra CDFE là hình chữ nhật.

d. Chứng minh rằng GDHB là hình bình hành, với BH cắt BD tại trung điểm của mỗi đường.

Câu 2:

a. Trong tứ giác BHCK, hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường. Do đó, tứ giác BHCK là hình bình hành.

b. Chứng minh rằng tam giác HIK có JM là đường trung bình, nên JM song song với IK và BC song song với IK, từ đó BIKC là hình thang cân.

3. Đề kiểm tra toán lớp 10 học kỳ 1 của sách Cánh Diều

I. Phần trắc nghiệm

Câu 1: Trong số các câu dưới đây, câu nào không phải là mệnh đề?

A. 12 là một số nguyên tố;

B. n không chia hết cho 2;

$x^{2}$

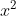
D. 10 là một số nguyên tố.

Câu 2: Với a thuộc (120; 270) thì giá trị lượng giác nào dưới đây là âm?

A. sin a

B. cos a

C. tan a

D. cot a

Câu 3: Trong lớp 10B có 45 học sinh, trong đó 25 em yêu thích môn Văn, 20 em yêu thích môn Toán, 18 em yêu thích môn Sử, 6 em không thích môn nào, 6 em thích cả Sử và Toán, 8 em thích cả Văn và Toán, 5 em thích cả ba môn. Số học sinh yêu thích cả Văn và Sử là

A. 5;

B. 10;

C. 12;

D. 15.

Câu 4: Tính giá trị của biểu thức: cos20 + cos40 + cos60 + ... + cos160 + cos180.

A. – 1;

B. 1;

C. 2;

D. 0.

Câu 5: Xét tam giác ABC với các cạnh AB = 5, BC = 7, CA = 8. Tam giác ABC thuộc loại nào?

A. Tam giác nhọn;

B. Tam giác tù;

C. Tam giác vuông;

D. Tam giác đều.

Câu 6. Với 90 < α < 180. Xác định dấu của biểu thức M = sin(90 – α).cot(180 + α).

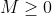
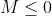
C. M > 0;

D. M < 0.

II. Phần tự luận

Bài 1. Một rạp chiếu phim có sức chứa 1 000 chỗ ngồi. Khi giá vé là 40 000 đồng, trung bình có khoảng 300 người đến xem phim mỗi ngày. Để tăng doanh thu, rạp chiếu phim đã khảo sát và phát hiện rằng mỗi khi giảm giá vé 10 000 đồng, số lượng khách đến xem phim tăng thêm 100 người mỗi ngày.

a) Tìm hàm số R(x) mô tả doanh thu hàng ngày từ việc bán vé khi giá vé là x nghìn đồng.

b) Xác định mức giá vé tối ưu để doanh thu từ việc bán vé hàng ngày là cao nhất.

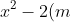
$x^{2} - 2(m + 3)x - 4m + 1$

Kết quả:

I. Trắc nghiệm

1. B

2. B

3. C

4. D

5. A

6. B

II. Phần tự luận

Câu 1:

a, Doanh thu từ việc bán vé hàng ngày của rạp được biểu diễn bằng hàm: R(x) = x(700 - 10x) (nghìn đồng)

b, Với giá vé 35 nghìn đồng, doanh thu từ việc bán vé mỗi ngày sẽ đạt mức cao nhất.

Câu 2:

Nội dung từ Mytour nhằm chăm sóc khách hàng và khuyến khích du lịch, chúng tôi không chịu trách nhiệm và không áp dụng cho mục đích khác.

Nếu bài viết sai sót hoặc không phù hợp, vui lòng liên hệ qua email: [email protected]