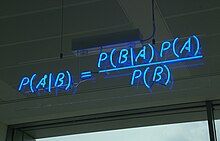
Định lý Bayes

Định lý Bayes (tiếng Anh: Bayes theorem) là một thành tựu quan trọng trong lý thuyết xác suất. Nó mô tả mối liên hệ giữa xác suất của một sự kiện mà không xét đến các yếu tố khác (gọi là xác suất biên hay xác suất tiên nghiệm) và xác suất của sự kiện đó khi một sự kiện khác đã xảy ra (gọi là xác suất có điều kiện hay xác suất hậu nghiệm). Cụ thể hơn, nó liên quan đến phân phối xác suất có điều kiện của một biến ngẫu nhiên A, với giả định:

• thông tin về một biến khác B: phân phối xác suất có điều kiện của B khi biết A, và
• phân phối xác suất của riêng A.

Phát biểu của định lý

Định lý Bayes giúp ta xác định xác suất xảy ra của một sự kiện ngẫu nhiên A dựa trên việc sự kiện liên quan B đã xảy ra. Xác suất này được ký hiệu là P(A|B), đọc là 'xác suất của A khi có B'. Đại lượng này được gọi là xác suất có điều kiện hay xác suất hậu nghiệm, vì nó được tính toán dựa trên thông tin từ B hoặc phụ thuộc vào giá trị của nó.

Theo định lý Bayes, xác suất của A khi biết B phụ thuộc vào 3 yếu tố chính:

• Xác suất xảy ra của A riêng lẻ, không phụ thuộc vào B. Ký hiệu là P(A) và đọc là 'xác suất của A'. Đây được gọi là xác suất biên hoặc xác suất tiên nghiệm, vì nó không dựa vào thông tin từ B.
• Xác suất xảy ra của B riêng lẻ, không liên quan đến A. Ký hiệu là P(B) và đọc là 'xác suất của B'. Đại lượng này còn được gọi là hằng số chuẩn hóa (normalizing constant), vì nó không thay đổi dù có hay không có sự kiện A.
• Xác suất xảy ra của B khi A đã xảy ra. Ký hiệu là P(B|A) và đọc là 'xác suất của B khi có A'. Đại lượng này gọi là khả năng (likelihood) xảy ra của B khi biết rằng A đã xảy ra. Lưu ý không nhầm lẫn giữa khả năng xảy ra của B khi biết A và xác suất xảy ra của A khi biết B.

Khi đã có ba đại lượng trên, xác suất của A khi biết B được tính theo công thức:

$P\left(A|B\right)=\frac{P\left(B|A\right)P\left(A\right)}{P\left(B\right)}=\frac{likelihood\ast <!--\; \ast \; -->prior}{normalizing\mathrm{\_<!--\; \_\; -->}constant}$

Từ đó, ta có thể suy ra

$P\left(A|B\right)P\left(B\right)=P(A\cap <!--\; \cap \; -->B)=P\left(B|A\right)P\left(A\right)$

{\displaystyle P(A|B)P(B)=P(A\cap B)=P(B|A)P(A)\,}

Các biến thể khác của định lý Bayes

Định lý Bayes cũng có thể được biểu diễn theo cách khác như sau

$P\left(B\right)=P(A,B)+P(A^C,B)=P\left(B|A\right)P\left(A\right)+P\left(B|A^C\right)P\left(A^C\right)$

hoặc

$P\left(A|B\right)=\frac{P\left(B|A\right)P\left(A\right)}{P\left(B|A\right)P\left(A\right)+P\left(B|A^C\right)P\left(A^C\right)},$

trong đó A là biến cố bổ sung của A (thường gọi là 'không A'). Đối với một phân hoạch tổng quát {A_i} của không gian các biến cố,

$P\left(A_i|B\right)=\frac{P\left(B|A_i\right)P\left(A_i\right)}{\underset{j}{\sum <!--\; \sum \; -->}P\left(B|A_j\right)P\left(A_j\right)},$

cho mọi A_i trong phân hoạch đó.

Công thức này còn được gọi là công thức xác suất toàn phần.

Định lý Bayes với hàm mật độ xác suất

Có một dạng của định lý Bayes áp dụng cho các phân phối liên tục. Trong trường hợp này, thay vì sử dụng xác suất, chúng ta sử dụng hàm mật độ xác suất. Do đó, các công thức trở nên tương tự như định nghĩa xác suất có điều kiện:

$f\left(x|y\right)=\frac{f\left(y|x\right)f\left(x\right)}{f\left(y\right)}$

và công thức tương tự như công thức xác suất toàn phần:

$f\left(x|y\right)=\frac{f\left(y|x\right)f\left(x\right)}{{\int <!--\; \int \; -->}_{-<!--\; -\; -->\mathrm{\infty <!--\; \infty \; -->}}^{\mathrm{\infty <!--\; \infty \; -->}}f\left(y|x^{\prime }\right)f\left(x^{\prime }\right)d{x}^{\prime }}.$

Các thành phần trong công thức trên được giải thích như sau: f(x, y) là hàm mật độ phân phối chung của các biến ngẫu nhiên X và Y, f(x|y) là hàm mật độ phân phối xác suất hậu nghiệm của X khi Y=y, f(y|x) = L(x|y) là hàm khả năng của X với điều kiện Y=y, và f(x) và f(y) là các hàm mật độ phân phối của X và Y, với f(x) là hàm mật độ phân phối tiền nghiệm của X.

Các công thức giả định rằng hàm f là khả vi và các tích phân trong công thức đều tồn tại.

Ứng dụng của định lý Bayes thường dựa trên quan điểm triết học của xác suất Bayesian, trong đó độ bất định và kỳ vọng được xem như các xác suất có thể tính toán được. Định lý này được đặt theo tên của Reverend Thomas Bayes (1702—1761), người đã nghiên cứu cách tính toán phân phối với tham số là phân phối nhị phân. Công trình của ông được người bạn Richard Price chỉnh sửa và công bố năm 1763, sau khi Bayes qua đời, với tiêu đề An Essay towards solving a Problem in the Doctrine of Chances. Pierre-Simon Laplace đã mở rộng kết quả này trong bài luận năm 1774.

• Bài toán Monty Hall
• Dao cạo của Occam
• Ngụy biện của người khởi tố
• Nghịch lý Hempel
• Cập nhật quan điểm trong thống kê

Các phiên bản gốc của bài luận của Bayes bằng tiếng Anh

• Thomas Bayes (1763), 'An Essay towards solving a Problem in the Doctrine of Chances', Philosophical Transactions of the Royal Society of London, 53.
• Thomas Bayes (1763/1958) 'Studies in the History of Probability and Statistics: IX. Thomas Bayes's Essay Towards Solving a Problem in the Doctrine of Chances', Biometrika 45:296-315 (bài luận của Bayes với ký hiệu hiện đại)
• Thomas Bayes 'An essay towards solving a Problem in the Doctrine of Chances' Lưu trữ 2011-04-10 tại Wayback Machine (bài luận của Bayes với ký hiệu gốc)

Những bình luận và tài liệu bổ sung

• G.A. Barnard. (1958) 'Studies in the History of Probability and Statistics: IX. Thomas Bayes's Essay Towards Solving a Problem in the Doctrine of Chances', Biometrika 45:293-295 (những ghi chú tiểu sử)
• Daniel Covarrubias 'An Essay Towards Solving a Problem in the Doctrine of Chances' Lưu trữ 2005-05-14 tại Wayback Machine (một bản phác thảo và giải thích bài luận của Bayes)
• Stephen M. Stigler (1982) 'Thomas Bayes' Bayesian Inference,' Journal of the Royal Statistical Society, Series A, 145:250-258 (Stigler đề xuất một cách giải thích sửa đổi bài luận -- được khuyến nghị)
• Isaac Todhunter (1865) A History of the Mathematical Theory of Probability from the time of Pascal to that of Laplace, Macmillan. Tái bản năm 1949, 1956 bởi Chelsea và 2001 bởi Thoemmes.

Các tài liệu tham khảo thêm

• Pierre-Simon Laplace (1774), 'Mémoire sur la Probabilité des Causes par les Événements,' Les Savants Étranges 6:621-656, cũng xuất hiện trong Oeuvres 8:27-65.
• Pierre-Simon Laplace (1774/1986), 'Memoir on the Probability of the Causes of Events', Statistical Science, 1(3):364–378.
• Stephen M. Stigler (1986), 'Bài luận của Laplace năm 1774 về xác suất nghịch đảo,' Statistical Science, 1(3):359–378.
• Stephen M. Stigler (1983), 'Ai phát hiện Định lý Bayes?' The American Statistician, 37(4):290-296.
• Jeff Miller. Những Sử Dụng Sớm Nhất Của Một Số Thuật Ngữ Toán Học (B) (rất thông tin -- được khuyến nghị)
• Athanasios Papoulis (1984), Xác Suất, Biến Ngẫu Nhiên, và Quy Trình Ngẫu Nhiên, phiên bản thứ hai. New York: McGraw-Hill.
• James Joyce. 'Định lý Bayes', trong Bách Khoa Toàn Thư Stanford.