1. Định lý Pytago là gì?
Mối liên hệ giữa các cạnh trong tam giác vuông đã được khám phá từ thời cổ đại, trước cả thời của Pytago, từ các nền văn minh như Ai Cập, Lưỡng Hà, Ấn Độ và Trung Hoa cổ đại. Tuy nhiên, định lý này chỉ được chứng minh và áp dụng rộng rãi trong toán học vào thời kỳ của nhà toán học Pytago ở Hy Lạp cổ đại. Định lý Pytago không chỉ có ứng dụng trong hình học cơ bản mà còn trong các lĩnh vực toán học khác như vi phân, tích phân, và hình học không gian, khiến nó trở thành một thành tựu quan trọng trong sự phát triển của toán học.
Định lý Pytago được sử dụng để tính toán độ dài các cạnh trong tam giác vuông. Đây là một liên hệ cơ bản trong hình học Euclid giữa ba cạnh của một tam giác vuông.
Định lý Pytago khẳng định rằng trong một tam giác vuông, bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại.
Ngược lại, định lý Pytago nghịch cho biết nếu bình phương của một cạnh trong tam giác bằng tổng bình phương của hai cạnh còn lại, thì tam giác đó là tam giác vuông.
Định lý Pytago còn được sử dụng để tạo ra các đoạn thẳng vô tỷ lệ, thể hiện các độ dài cạnh của tam giác vuông mà cả ba độ dài này là số nguyên dương.
2. Công thức của định lý Pytago
Xét tam giác ABC vuông tại điểm A, với các cạnh AB = a, AC = b, và BC = c. Theo định lý Pytago, mối quan hệ giữa các cạnh trong tam giác được diễn tả như sau:
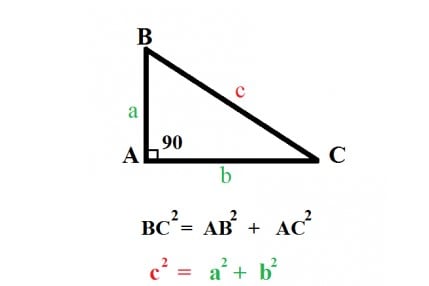
Khi biết độ dài của hai cạnh trong tam giác vuông, ta có thể tính được độ dài của cạnh còn lại nhờ vào định lý Pytago.
Công thức định lý Pytago đảo ngược:
Nếu trong tam giác ABC, bình phương của độ dài cạnh BC bằng tổng bình phương của hai cạnh AB và AC, thì góc BAC là 90 độ.
Định lý Pytago đảo được dùng để nhận diện tam giác vuông. Để giải loại bài tập này, bạn có thể làm theo các bước sau:
- Tính bình phương của ba cạnh trong tam giác.
- So sánh bình phương của cạnh dài nhất với tổng của bình phương hai cạnh còn lại.
- Nếu hai kết quả là như nhau thì tam giác đó là tam giác vuông với cạnh dài nhất là cạnh huyền.
3. Phương pháp chứng minh định lý Pytago
Chúng ta có thể dễ dàng chứng minh định lý Pytago qua hình minh họa dưới đây:
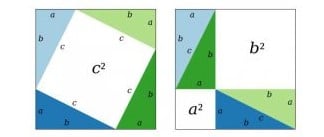
Trong hình trên, chúng ta có hai hình vuông lớn với diện tích bằng nhau là ( a + b ) ^ 2
Mỗi hình bao gồm 4 tam giác vuông có diện tích đồng đều là 1/2 (a.b). Vì vậy, diện tích phần trống giữa hai hình là bằng nhau.
Như vậy, diện tích của hình vuông c sẽ bằng tổng diện tích của hai hình vuông a và b, từ đó ta có: c ^ 2 = a ^ 2 + b ^ 2
Phương pháp này cũng được áp dụng để giải bài 7 trang 129 trong sách giáo khoa Toán lớp 7 tập 1.
4. Bài tập áp dụng định lý Pytago theo chương trình Toán lớp 7
Bài tập 1: Xác định độ dài x trong hình minh họa dưới đây:
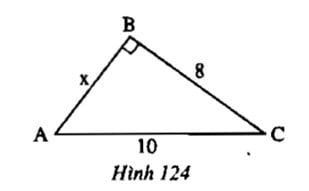
Hướng dẫn giải:
Áp dụng định lý Pytago, ta có công thức sau:
Tam giác ABC vuông tại điểm B
=> x ^ 2 + 8 ^ 2 = 10 ^ 2
=> x ^ 2 = 10 ^ 2 - 8 ^ 2 = 6 ^ 2 = 36
=> x = 6 cm
Bài tập 2: Cho tam giác ABC với AC = 5 cm, BC = 3 cm và AB = 4 cm. Tam giác ABC thuộc loại nào?
Hướng dẫn giải:
Chúng ta có: AC ^ 2 = BC ^ 2 + AB ^ 2 (vì 5 ^ 2 = 3 ^ 2 + 4 ^ 2)
Tam giác ABC là tam giác vuông tại B (theo định lý Pytago đảo).
Bài tập 3: Xem xét tam giác ABC vuông tại A:
1. Nếu cạnh AB dài 4 cm và cạnh BC dài 6 cm, hãy tính chiều dài cạnh AC
2. Nếu cạnh AC dài 2 cm và cạnh BC dài 7 cm, hãy tính chiều dài cạnh AB
3. Nếu cạnh AB dài 3 cm và cạnh AC dài 5 cm, hãy tính chiều dài cạnh BC
Hướng dẫn cách giải:
1. Theo định lý Pytago: BC ^ 2 = AC ^ 2 + AB ^ 2
=> AC ^ 2 = BC ^ 2 - AB ^ 2
=> AC ^ 2 = 6 ^ 2 - 4 ^ 2
=> AC = căn bậc hai của 20 (cm).
2. Theo định lý Pytago: BC ^ 2 = AC ^ 2 + AB ^ 2
=> AB ^ 2 = BC ^ 2 - AC ^ 2
=> AB ^ 2 = 7 ^ 2 - 2 ^ 2
=> AB = căn bậc hai của 45 (cm).
3. Theo định lý Pytago: BC ^ 2 = AC ^ 2 + AB ^ 2
=> BC ^ 2 = 3 ^ 2 + 5 ^ 2
=> BC = căn bậc hai của 34 (cm)
Bài tập 4: Xác định chiều dài cạnh huyền trong các tam giác sau, biết rằng:
a. Tam giác MNO vuông tại M với cạnh MO dài 4 cm và cạnh MN dài 5 cm
b. Tam giác PQR vuông tại P với cạnh PQ dài 7 cm và cạnh PR dài 6 cm
c. Tam giác BCD vuông tại B với cạnh BC dài 8 cm và cạnh BD dài 2 cm
d. Tam giác IKL vuông tại I với cạnh IL dài 4,5 cm và cạnh IK dài 8 cm
Hướng dẫn cách giải:
a. Trong tam giác MNO vuông tại M, NO là cạnh huyền, nên ta sử dụng định lý Pytago để tính toán:
NO ^ 2 = MN ^ 2 + MO ^ 2
=> NO ^ 2 = 4 ^ 2 + 5 ^ 2
=> NO ^ 2 = 41
=> NO = căn bậc hai của 41 (cm), xấp xỉ 6,4 cm
b. Trong tam giác PQR vuông tại P, với QR là cạnh huyền, ta áp dụng định lý Pytago như sau:
QR ^ 2 = PQ ^ 2 + PR ^ 2
=> QR ^ 2 = 7 ^ 2 + 6 ^ 2
=> QR ^ 2 = 85
=> QR = căn bậc hai của 85 (cm), khoảng 9,2 cm
c. Trong tam giác BCD vuông tại B, với CD là cạnh huyền, ta áp dụng định lý Pytago như sau:
CD ^ 2 = BC ^ 2 + BD ^ 2
=> CD ^ 2 = 8 ^ 2 + 2 ^ 2
=> CD ^ 2 = 70
=> CD = căn bậc hai của 70 (cm), xấp xỉ 8,4 cm
d. Trong tam giác IKL vuông tại I, với KL là cạnh huyền, ta áp dụng định lý Pytago như sau:
KL ^ 2 = IL ^ 2 + IK ^ 2
=> KL ^ 2 = 4,5 ^ 2 + 8 ^ 2
=> KL ^ 2 = 84,25
=> KL = căn bậc hai của 84,25 (cm), xấp xỉ 9,2 cm
Bài tập 5: Tính chiều cao của bức tường, biết thang dài 4m và chân thang cách tường 1m.
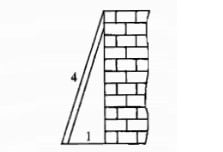
Hướng dẫn cách giải:
Vì mặt đất vuông góc với chân tường, nên góc C là 90 độ
Áp dụng định lý Pytago cho tam giác vuông ABC (vuông tại C), ta có:
AC ^ 2 + BC ^ 2 = AB ^ 2
=> AC ^ 2 = AB ^ 2 - BC ^ 2 = 4 ^ 2 - 1 ^ 2 = 16 - 1 = 15
=> AC = căn bậc hai của 15 (m), xấp xỉ 3,87 (m).
Do đó, chiều cao của bức tường là 3,87 m.
Hy vọng bài viết của Mytour về Định lý Pytago: Công thức và bài tập áp dụng trong Toán lớp 7 đã giúp Quý bạn đọc hiểu rõ hơn và củng cố kiến thức. Mong rằng Mytour sẽ tiếp tục đồng hành cùng Quý bạn đọc trong những bài viết tiếp theo. Xin chân thành cảm ơn!
