Định lý Pythagoras

Trong hình học, định lý Pythagoras (còn gọi là định lý Py-ta-go) mô tả mối quan hệ cơ bản giữa ba cạnh của một tam giác vuông. Theo định lý, bình phương cạnh huyền (cạnh đối diện góc vuông) bằng tổng bình phương của hai cạnh còn lại. Định lý có thể được diễn đạt bằng phương trình liên hệ các độ dài cạnh a, b và c, thường được gọi là 'công thức Pythagoras': Đây là kiến thức cơ bản mà học sinh lớp 7 ở Việt Nam học theo sách giáo khoa chương trình giáo dục phổ thông năm 2006.

$c^2=a^2+b^2;$

với c là độ dài của cạnh huyền, và a, b là độ dài của hai cạnh góc vuông, thường được gọi là cạnh kề.

Mặc dù mối liên hệ này đã được biết đến từ trước thời của Pythagoras, định lý vẫn mang tên ông, nhà toán học Hy Lạp cổ đại (k. 570–495 TCN). Ông được ghi nhận là người đầu tiên chứng minh định lý này dựa trên các tài liệu lịch sử. Có bằng chứng cho thấy các nhà toán học Babylon đã biết đến công thức này, dù không có nhiều tài liệu về việc họ áp dụng nó trong toán học. Các nền văn minh ở Lưỡng Hà, Ấn Độ và Trung Quốc cũng đã tự khám phá định lý này và chứng minh cho một số trường hợp đặc biệt.

Có vô số cách chứng minh định lý này, có thể là nhiều nhất trong toán học. Các phương pháp chứng minh rất đa dạng, bao gồm cả hình học và đại số, nhiều trong số đó có lịch sử hàng nghìn năm. Định lý Pythagoras cũng được mở rộng trong nhiều cách khác nhau, từ không gian nhiều chiều đến các không gian phi Euclid, từ tam giác vuông đến các đối tượng hình học tổng quát. Định lý này cũng thu hút sự chú ý không chỉ trong toán học mà còn trong văn học, âm nhạc, phim ảnh, và các lĩnh vực khác như con tem và hoạt hình.

Chứng minh của Pythagoras

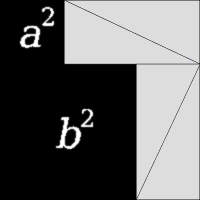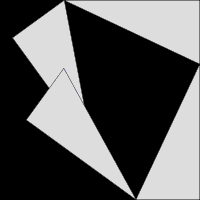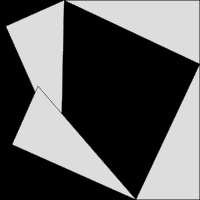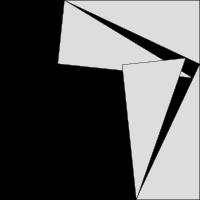
Định lý Pythagoras đã được biết đến từ lâu trước thời Pythagoras, nhưng ông được xem là người đầu tiên đưa ra chứng minh định lý này. Cách chứng minh của ông rất đơn giản, chỉ cần tái sắp xếp các hình vẽ.

Trong hai hình vuông lớn trong hình minh họa bên trái, mỗi hình vuông chứa bốn tam giác vuông giống hệt nhau, chỉ khác nhau ở cách sắp xếp các tam giác vuông. Do đó, diện tích các khoảng trống bên trong mỗi hình vuông phải bằng nhau. Dựa vào hình vẽ, diện tích các vùng trắng bằng nhau giúp chúng ta chứng minh định lý Pythagoras.

Sau này, nhà triết học và toán học Hy Lạp Proclus đã đưa ra một chứng minh đơn giản của Pythagoras trong tác phẩm của ông. Dưới đây là một số cách chứng minh khác, nhưng chứng minh ở trên thuộc về Pythagoras.

Các dạng khác của định lý

Như đã đề cập trong phần giới thiệu, nếu c là chiều dài của cạnh huyền và a và b là chiều dài của hai cạnh kề, định lý Pythagoras có thể được biểu diễn bằng phương trình sau:

$c^2=a^2+b^2$

Nếu bạn đã biết chiều dài của hai cạnh a và b, thì cạnh huyền c có thể tính bằng công thức:

$c=\sqrt{a^2+b^2}.$

Nếu bạn biết chiều dài của cạnh huyền c và một trong các cạnh kề (a hoặc b), bạn có thể tính chiều dài của cạnh còn lại bằng cách sử dụng công thức sau: $a=\sqrt{c^2-b^2}$hoặc $b=\sqrt{c^2-a^2}.$

Phương trình của định lý Pythagoras đơn giản hóa việc tìm chiều dài của các cạnh trong tam giác vuông, cho phép bạn xác định cạnh còn lại khi biết chiều dài của hai cạnh khác. Một hệ quả quan trọng của định lý này là trong mọi tam giác vuông, cạnh huyền luôn lớn hơn hai cạnh còn lại nhưng nhỏ hơn tổng của chúng.

Định lý Pythagoras có thể được mở rộng thành định lý cos cho các tam giác bất kỳ, cho phép tính toán chiều dài của một cạnh khi biết chiều dài của hai cạnh còn lại và góc giữa chúng. Trong trường hợp góc giữa hai cạnh là góc vuông, định lý cos trở thành định lý Pythagoras.

Các phương pháp chứng minh khác

Định lý này nổi bật với số lượng cách chứng minh phong phú; ví dụ, trong cuốn sách The Pythagorean Proposition, có tới 370 phương pháp chứng minh cho định lý Pythagoras.

Chứng minh bằng cách sử dụng các tam giác đồng dạng

Chứng minh này dựa vào tính chất tỉ lệ của các cạnh trong hai tam giác đồng dạng, tức là tỉ lệ giữa các cạnh tương ứng của chúng là không đổi, bất kể kích thước của tam giác.

Xem xét tam giác ACB với góc vuông tại đỉnh A, như trong hình minh họa. Vẽ đường cao từ điểm C và ký hiệu H là chân đường cao trên cạnh AB. Điểm H chia cạnh huyền c thành hai đoạn là AH và BH. Tam giác ACH đồng dạng với tam giác ABC vì cả hai đều có góc vuông và góc chung tại đỉnh A, dẫn đến góc còn lại cũng tương đương, ký hiệu là θ. Tương tự, tam giác CBH cũng đồng dạng với tam giác ABC. Để chứng minh sự đồng dạng, ta dựa vào định lý về tổng góc trong tam giác và tiên đề về hai đường thẳng song song. Sự đồng dạng cho thấy tỷ số của các cạnh tương ứng là bằng nhau.

$\frac{BC}{AB}=\frac{BH}{BC}$ và $\frac{AC}{AB}=\frac{AH}{AC}.$

Tỷ số đầu tiên tương ứng với cosin của góc θ, trong khi tỷ số thứ hai tương ứng với sin của góc này.

Ghi lại các tỷ số này

$B{C}^2=AB\times <!--\; \times \; -->BH$ và $A{C}^2=AB\times <!--\; \times \; -->AH.$

Cộng hai vế của hai phương trình đã cho

$B{C}^2+A{C}^2=AB\times <!--\; \times \; -->BH+AB\times <!--\; \times \; -->AH=AB\times <!--\; \times \; -->(AH+BH)=A{B}^2,$

Và từ đó chúng ta có được định lý Pythagoras:

$B{C}^2+A{C}^2=A{B}^2$

Nhiều ý kiến khác nhau đã được đưa ra về vai trò của chứng minh này trong lịch sử toán học. Một số người đặt câu hỏi tại sao Euclid không sử dụng chứng minh này mà chọn một phương pháp khác. Một giả thuyết cho rằng chứng minh bằng cách sử dụng tam giác đồng dạng liên quan đến định lý về tỷ lệ, một chủ đề chưa được phát triển cho đến khi ông viết cuốn Cơ sở (Elements), và định lý về tỷ lệ cần được phát triển thêm vào thời điểm đó.

Chứng minh theo cách của Euclid

Tóm tắt chứng minh của Euclid như được mô tả trong cuốn Elements. Hình vuông lớn (với cạnh là cạnh huyền) được phân chia thành hai hình chữ nhật nằm ở hai bên (xem hình minh họa).

Xây dựng một tam giác có diện tích bằng một nửa diện tích của hình chữ nhật bên trái. Tiếp theo, xây dựng một tam giác khác có diện tích bằng một nửa diện tích của hình vuông trên cạnh bên trái. Chứng minh hai tam giác này bằng nhau, từ đó cho thấy diện tích của hình vuông bên trái bằng diện tích của hình chữ nhật bên trái. Lặp lại quy trình tương tự cho hình vuông và hình chữ nhật bên phải. Tổng diện tích của hai hình chữ nhật bằng diện tích của hình vuông trên cạnh huyền, và cũng chính bằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông. Chi tiết của chứng minh như sau.

Cho A, B, C là các đỉnh của một tam giác vuông với góc vuông tại A. Kẻ một đường thẳng từ A vuông góc với cạnh huyền. Đường thẳng này chia hình vuông dựng trên cạnh huyền thành hai hình chữ nhật, và chứng minh rằng diện tích của hai hình chữ nhật này lần lượt bằng diện tích của hai hình vuông trên hai cạnh góc vuông.

Để có một chứng minh chặt chẽ, cần dựa vào bốn bổ đề cơ bản dưới đây:

1. Nếu hai tam giác có hai cạnh tương ứng bằng nhau và góc giữa chúng cũng bằng nhau, thì hai tam giác đó bằng nhau (trường hợp cạnh-góc-cạnh).
2. Diện tích của một tam giác bằng một nửa diện tích của hình bình hành có cùng đáy và chiều cao.
3. Diện tích của hình chữ nhật bằng tích của hai cạnh kề.
4. Diện tích của hình vuông bằng bình phương cạnh của nó (hệ quả từ bổ đề 3).

Tiếp theo, mỗi hình vuông được dựng trên các cạnh kề sẽ được liên kết với một tam giác tương đương, mà tam giác này cũng tương đương với một hình chữ nhật vừa được phân chia.

Chứng minh như sau:

1. Gọi tam giác ABC là tam giác vuông tại góc CAB.
2. Trên các cạnh BC, AB và CA, chúng ta dựng các hình vuông CBDE, BAGF và ACIH tương ứng. Việc dựng các hình vuông này dựa trực tiếp vào các định lý đã nêu trong sách của Euclid và tiên đề về các đường thẳng song song.
3. Từ đỉnh A, vẽ một đường thẳng song song với hai cạnh BD và CE. Đường này sẽ vuông góc với BC và DE, cắt chúng tại các điểm K và L.
4. Nối CF và AD để tạo ra hai tam giác BCF và BDA.
5. Góc CAB và BAG đều là các góc vuông, vì vậy các điểm C, A, và G nằm trên cùng một đường thẳng, tương tự đối với các điểm B, A, và H.
6. Góc CBD và FBA đều là góc vuông, từ đó suy ra góc ABD bằng góc FBC vì cả hai đều bằng tổng của một góc vuông với góc ABC.
7. Do AB bằng FB và BD bằng BC, nên hai tam giác ABD và FBC bằng nhau.
8. Vì A-K-L là đường thẳng song song với cạnh BD, hình chữ nhật BDLK có diện tích gấp hai lần diện tích tam giác ABD do chúng cùng có cạnh đáy BD và cùng chiều cao BK, vuông góc với cạnh đáy và nối hai đường thẳng song song BD và AL. (bổ đề 2)
9. Vì C nằm trên cùng đường thẳng với A và G, nên diện tích hình vuông BAGF gấp hai lần diện tích tam giác FBC.
10. Từ đó, diện tích hình chữ nhật BDLK bằng diện tích hình vuông BAGF = AB.
11. Tương tự, hình chữ nhật CKLE có diện tích bằng diện tích hình vuông ACIH = AC.
12. Cộng hai kết quả lại, ta có AB + AC = BD × BK + KL × KC
13. Vì BD = KL, ta có BD × BK + KL × KC = BD(BK + KC) = BD × BC
14. Do đó, AB + AC = BC, vì CBDE là hình vuông.

Chứng minh này được trình bày trong Định đề 47 của tập 1 cuốn Cơ sở của Euclid, chứng minh rằng diện tích hình vuông trên cạnh huyền bằng tổng diện tích của hai hình vuông trên hai cạnh kề. Phương pháp chứng minh này khác biệt so với cách dựa vào tam giác đồng dạng mà Pythagoras đã sử dụng để chứng minh định lý.

Các phương pháp chứng minh bằng cách chia và sắp xếp lại hình

Như đã thảo luận về chứng minh định lý Pythagoras bằng phương pháp sắp xếp lại hình, một ý tưởng tương tự cũng được sử dụng trong chứng minh được mô tả bằng hình động bên trái. Ban đầu có một hình vuông lớn với cạnh bằng a + b, bên trong là bốn tam giác vuông bằng nhau. Hình động cho thấy có hai cách sắp xếp khác nhau của các tam giác này, cách đầu tiên tạo thành hai hình vuông có cạnh lần lượt là a và b, cách thứ hai chỉ tạo thành một hình vuông có cạnh c. Vì hình vuông bao ngoài không thay đổi và diện tích của bốn tam giác là như nhau trong cả hai cách sắp xếp, diện tích của các hình vuông nhỏ màu đen phải bằng nhau, do đó a + b = c.

Cách chứng minh thứ hai được minh họa qua hình động thứ hai. Một hình vuông lớn có diện tích c được tạo thành từ bốn tam giác vuông bằng nhau với các cạnh a, b, và c, xung quanh một hình vuông nhỏ nằm ở trung tâm. Khi sắp xếp lại các tam giác, ta thu được hai hình chữ nhật với các cạnh lần lượt là a và b. Kết hợp hình vuông nhỏ với hai hình chữ nhật này tạo thành hai hình vuông có diện tích tương ứng là a và b, và chúng phải có diện tích bằng hình vuông lớn ban đầu.

Cách thứ ba được mô tả trong hình động ngoài cùng. Hai hình vuông ở trên được chia thành các mảnh màu xanh lục và xanh lam, khi sắp xếp lại các mảnh này có thể vừa khít với hình vuông ở dưới có cạnh là cạnh huyền của tam giác vuông. Ngược lại, hình vuông lớn ở dưới có thể được chia thành các mảnh nhỏ và khi sắp xếp lại các mảnh này có thể vừa khít vào hai hình vuông nằm trên hai cạnh của góc vuông. Phương pháp chia một hình thành các phần nhỏ và sắp xếp chúng lại để tạo thành hình khác được gọi là bài toán phân chia (dissection problem). Từ đó, ta kết luận rằng diện tích của hình vuông lớn phải bằng tổng diện tích của hai hình vuông nhỏ.

Chứng minh của Einstein bằng cách phân tích lập luận

Khi còn 11 tuổi, Albert Einstein đã đưa ra một phương pháp chứng minh bằng phân chia mà không cần di chuyển hay sắp xếp lại các hình. Thay vì dùng một hình vuông trên cạnh huyền và hai hình vuông trên các cạnh kề, ông sử dụng một hình khác bao gồm cạnh huyền và hai hình đồng dạng có một cạnh là cạnh kề thay cho cạnh huyền. Trong chứng minh của Einstein, hình bao gồm cạnh huyền chính là tam giác vuông lớn ban đầu. Khi phân chia tam giác này bằng cách hạ đường cao từ đỉnh góc vuông xuống cạnh huyền, ta thu được hai tam giác vuông nhỏ hơn. Hai tam giác vuông này đồng dạng với tam giác vuông ban đầu, với cạnh huyền là cạnh góc vuông của tam giác ban đầu, và tổng diện tích của chúng bằng diện tích tam giác ban đầu. Bởi vì tỉ lệ diện tích của một tam giác vuông so với diện tích hình vuông dựng trên cạnh huyền của nó là bằng nhau với các tam giác đồng dạng, mối quan hệ diện tích giữa ba tam giác cũng thỏa mãn với các hình vuông dựng trên các cạnh của hình vuông lớn.

Chứng minh bằng đại số

Định lý có thể được chứng minh bằng phương pháp đại số với bốn tam giác vuông bằng nhau có cạnh a, b, và c, được sắp xếp trong một hình vuông có cạnh c như trong hình trên. Các tam giác này có diện tích $\frac{1}{2}ab$, trong khi hình vuông nhỏ có cạnh b − a và diện tích (b − a). Diện tích của hình vuông lớn là:$(b-<!--\; -\; -->a{)}^2+4\frac{ab}{2}=(b-<!--\; -\; -->a{)}^2+2ab=b^2-<!--\; -\; -->2ab+a^2+2ab=a^2+b^2.$

Hình vuông này có cạnh c và diện tích bằng c, vì vậy

$c^2=a^2+b^2.$

Chứng minh cũng có thể thực hiện bằng cách sử dụng bốn tam giác vuông bằng nhau sắp xếp đối xứng quanh một hình vuông với cạnh c, như hình dưới đây. Kết quả cho một hình vuông lớn hơn, với cạnh a + b và diện tích (a + b). Tổng diện tích của bốn tam giác và hình vuông cạnh c bằng diện tích của hình vuông lớn hơn,

${\left(b+a\right)}^2=c^2+4\cdot <!--\; \cdot \; -->\frac{ab}{2}=c^2+2ab,$

do đó

$c^2=(b+a{)}^2-<!--\; -\; -->2ab=b^2+2ab+a^2-<!--\; -\; -->2ab=a^2+b^2.$

Trước khi trở thành Tổng thống Hoa Kỳ, James A. Garfield (khi đó là Hạ nghị sĩ) đã đề xuất một phương pháp chứng minh định lý Pythagoras. Thay vì sử dụng hình vuông, ông đã chọn hình thang, được tạo ra từ hình vuông trong chứng minh trước bằng cách chia nó theo đường chéo của hình vuông bên trong, tạo thành hình thang như trong hình vẽ. Diện tích của hình thang tương đương một nửa diện tích hình vuông, và được tính bằng

$\frac{1}{2}(b+a{)}^2.$

Hình vuông bên trong cũng bị chia đôi diện tích, và chỉ còn lại hai tam giác vuông, nên ta có đẳng thức sau đây:

$\frac{1}{2}{\left(b+a\right)}^2=\frac{1}{2}{c}^2+2\left(\frac{1}{2}ab\right)$

Sau khi rút gọn đẳng thức, ta có được điều cần chứng minh.

Chứng minh bằng phương pháp vi tích phân

Có thể chứng minh định lý Pythagoras bằng cách khảo sát sự thay đổi của cạnh kề và ảnh hưởng của nó đối với cạnh huyền, áp dụng phương pháp vi tích phân để phân tích.

Tam giác vuông ABC có cạnh huyền BC. Ban đầu, cạnh huyền có độ dài y, cạnh kề AC dài x, và cạnh AB dài a, như minh họa trong hình dưới đây.

Nếu x được kéo dài thêm một lượng vi phân dx bằng cách mở rộng AC đến điểm D, thì y cũng tăng thêm một lượng vi phân dy. Hai cạnh mới tạo thành một tam giác CDE, trong đó (với E được chọn sao cho CE vuông góc với cạnh huyền) là tam giác gần đồng dạng với ABC. Vì vậy, tỉ số giữa các cạnh phải gần như bằng nhau, tức là:

$\frac{dy}{dx}=\frac{x}{y}.$

Biểu thức có thể được viết lại thành $ydy=xdx$, đây là phương trình vi phân có thể giải bằng cách thực hiện tích phân hai vế.

$\int <!--\; \int \; -->ydy=\int <!--\; \int \; -->xdx,$

và thu được

$y^2=x^2+C.$

Hằng số tích phân được xác định khi x = 0, thì y = a, từ đó ta có phương trình

$y^2=x^2+a^2.$

Chứng minh trên chỉ là minh họa trực quan để dễ hiểu. Để có chứng minh chặt chẽ hơn (nhưng có thể khó đọc hơn đối với người không chuyên về vi tích phân), ta có thể chuyển từ tích phân không xác định sang tích phân xác định.

Định lý đảo

Định lý đảo của định lý Pythagoras cũng đúng:

Với ba số thực dương bất kỳ a, b, và c sao cho a + b = c, có thể tạo ra một tam giác với ba cạnh lần lượt là a, b và c, và trong tam giác đó, góc giữa hai cạnh a và b luôn là góc vuông.

Một cách phát biểu khác của định lý đảo:

Đối với bất kỳ tam giác nào có ba cạnh a, b, và c, nếu a + b = c, thì góc giữa hai cạnh a và b sẽ là 90°.

Định lý đảo cũng được Euclid đề cập trong cuốn Cơ sở (tập I, mệnh đề 48):

'Nếu trong một tam giác, bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại, thì góc được tạo bởi hai cạnh này là góc vuông.'

Có thể chứng minh định lý đảo của Pythagoras bằng cách áp dụng định lý cos hoặc qua cách chứng minh dưới đây:

Xét tam giác ABC với các cạnh a, b, và c, trong đó a + b = c. Ta dựng một tam giác khác với hai cạnh bằng a và b, và một góc vuông giữa chúng. Theo định lý Pythagoras thuận, cạnh huyền của tam giác vuông này sẽ là c = √a + b, bằng với cạnh huyền của tam giác đầu tiên. Vì hai tam giác đều có ba cạnh tương ứng bằng a, b và c, chúng là bằng nhau. Do đó, góc giữa hai cạnh a và b trong tam giác đầu tiên là góc vuông.

Chứng minh định lý đảo nêu trên dựa vào định lý Pythagoras. Cũng có thể thực hiện chứng minh này mà không cần sử dụng định lý Pythagoras thuận.

Một hệ quả của định lý Pythagoras đảo là cách dễ dàng để xác định tam giác là vuông hay không, hoặc nó thuộc loại nhọn hay tù. Xét c là cạnh dài nhất của tam giác và đảm bảo rằng a + b > c (nếu không, tam giác sẽ không tồn tại do đây là bất đẳng thức tam giác). Các phát biểu sau đây sẽ đúng:

• Nếu a + b = c, tam giác là tam giác vuông.
• Nếu a + b > c, tam giác là tam giác nhọn.
• Nếu a + b < c, tam giác là tam giác tù.

Edsger W. Dijkstra đã trình bày các định lý về tam giác nhọn, vuông và tù bằng các ký hiệu sau đây:

sgn(α + β − γ) = sgn(a + b − c),

Trong đó, α là góc đối diện với cạnh a, β là góc đối diện với cạnh b, γ là góc đối diện với cạnh c, và sgn là hàm signum.

Các hệ quả và ứng dụng

Những bộ số Pythagoras

Một bộ ba số Pythagoras là ba số nguyên dương a, b, và c, sao cho a + b = c. Nói cách khác, đây là các độ dài của ba cạnh của một tam giác vuông mà tất cả các cạnh đều là số nguyên dương. Các khám phá khảo cổ học ở miền bắc châu Âu cho thấy rằng các bộ ba này đã được biết đến từ thời cổ đại trước khi có các tài liệu ghi chép. Những bộ ba này thường được biểu diễn dưới dạng (a, b, c). Ví dụ về các bộ ba phổ biến là (3, 4, 5) và (5, 12, 13).

Một bộ ba số Pythagoras được gọi là bộ ba nguyên thủy khi các số a, b và c không có ước số chung lớn hơn 1 (tức là ước số chung lớn nhất của a, b và c bằng 1).

Dưới đây là danh sách các bộ ba số Pythagoras nguyên thủy nhỏ hơn 100 (tổng cộng 16 bộ):

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Vẽ đoạn thẳng không đo được

Một hệ quả quan trọng của định lý Pythagoras là khả năng dựng các đoạn thẳng vô tỷ (tỉ số của chúng không phải là một số hữu tỉ) bằng thước và compa. Định lý cho phép thực hiện điều này nhờ vào việc tính toán căn bậc hai của cạnh huyền trong tam giác vuông, từ đó liên hệ với hai cạnh kề.

Hình bên phải minh họa cách tạo ra các đoạn thẳng có độ dài là căn bậc hai của một số nguyên dương bất kỳ. Mỗi tam giác có một cạnh (được đánh dấu là '1') có độ dài bằng một đơn vị. Trong mỗi tam giác vuông, định lý Pythagoras cho phép xác định cạnh huyền dựa trên độ dài đơn vị của cạnh kề. Nếu cạnh huyền tương ứng với căn bậc hai của một số nguyên dương không phải là số chính phương, tức là độ dài của nó là vô tỷ so với chiều dài đơn vị, như √2, √3, √5. Xem thêm về số vô tỉ bậc hai.

Độ dài vô tỷ gây mâu thuẫn với quan niệm của trường phái Pythagoras về các số hoàn thiện. Trường phái này chỉ xem xét các tỷ số giữa các số nguyên với một đơn vị chung. Theo truyền thuyết, triết gia Hippasus của Metapontum (khoảng 470 trước Công nguyên) đã bị trừng phạt bằng cách bị ném xuống biển vì phát hiện ra sự tồn tại của số vô tỉ hay đoạn thẳng vô tỷ.

Số phức

Xét một số phức bất kỳ

$z=x+iy,$

thì trị tuyệt đối hay mô-đun của số phức đó được tính bằng

$r=|z|=\sqrt{x^2+y^2}.$

Vì vậy, ba đại lượng r, x và y được liên kết qua phương trình Pythagoras,

$r^2=x^2+y^2.$

Lưu ý rằng r luôn là một số thực dương hoặc bằng 0, trong khi x và y có thể là số dương hoặc âm. Về mặt hình học, r chính là khoảng cách từ z đến điểm gốc tọa độ O trong mặt phẳng phức.

Dựa trên định nghĩa trên, chúng ta có thể tính khoảng cách giữa hai điểm, chẳng hạn như z₁ và z₂. Khoảng cách này được tính bằng

$|z_1-<!--\; -\; -->z_2|=\sqrt{(x_1-<!--\; -\; -->x_2{)}^2+(y_1-<!--\; -\; -->y_2{)}^2},$

Đây chính là phương trình Pythagoras dưới một dạng khác,

$|z_1-<!--\; -\; -->z_2{|}^2=(x_1-<!--\; -\; -->x_2{)}^2+(y_1-<!--\; -\; -->y_2{)}^2.$

Khoảng cách Euclid trong các hệ tọa độ khác nhau

Khoảng cách giữa hai điểm trong hệ tọa độ Descartes được xác định dựa trên định lý Pythagoras. Nếu (x₁, y₁) và (x₂, y₂) là tọa độ của hai điểm trên mặt phẳng, khoảng cách giữa chúng được tính bằng, hay còn gọi là khoảng cách Euclid:

$\sqrt{(x_1-<!--\; -\; -->x_2{)}^2+(y_1-<!--\; -\; -->y_2{)}^2}.$

Trong không gian Euclid n chiều, khoảng cách Euclid giữa hai điểm, A và B, được tính dựa trên định lý Pythagoras mở rộng. Điểm A có tọa độ (a₁, a₂, …, aₙ) và điểm B có tọa độ (b₁, b₂, …, bₙ).

Khoảng cách Euclid giữa hai điểm A và B trong không gian n chiều được tính bằng công thức tổng quát hóa định lý Pythagoras: √((a₁−b₁)² + (a₂−b₂)² + … + (aₙ−bₙ)²).

Khi không sử dụng hệ tọa độ Descartes mà áp dụng hệ tọa độ cực cho không gian hai chiều, hoặc hệ tọa độ cong tổng quát hơn, công thức tính khoảng cách Euclid sẽ trở nên phức tạp hơn so với định lý Pythagoras. Tuy nhiên, công thức vẫn có thể được suy ra bằng cách sử dụng định lý Pythagoras kết hợp với phép biến đổi từ hệ tọa độ cong sang hệ tọa độ Descartes. Ví dụ, trong hệ tọa độ cong (r, θ), mối quan hệ với tọa độ Descartes là:

Trong hệ tọa độ cong, tọa độ Descartes của điểm (r, θ) được tính bằng x = r * cos(θ) và y = r * sin(θ).

Và khoảng cách giữa hai điểm có tọa độ (r₁, θ₁) và (r₂, θ₂) là s.

Khoảng cách giữa hai điểm trong hệ tọa độ Descartes và hệ tọa độ cực có thể được tính bằng công thức sau: s² = (x₁ − x₂)² + (y₁ − y₂)² = (r₁ cos θ₁ − r₂ cos θ₂)² + (r₁ sin θ₁ − r₂ sin θ₂)².

Sau khi khai triển bình phương và kết hợp các hạng tử, công thức Pythagoras cho khoảng cách trong hệ tọa độ Descartes có thể chuyển thành công thức khoảng cách trong hệ tọa độ cực như sau:

Khoảng cách giữa hai điểm trong hệ tọa độ cực có thể được tính bằng công thức: s² = r₁² + r₂² − 2r₁r₂ (cos θ₁ cos θ₂ + sin θ₁ sin θ₂) = r₁² + r₂² − 2r₁r₂ cos (θ₁ − θ₂) = r₁² + r₂² − 2r₁r₂ cos Δθ.

Bằng cách áp dụng định lý cos để chuyển đổi từ dạng tích thành dạng tổng, ta có công thức tổng quát cho định lý Pythagoras. Trong trường hợp hai bán kính tạo thành góc vuông, tức là Δθ = π/2, công thức Pythagoras sẽ trở thành: s² = r₁² + r₂². Đây là trường hợp đặc biệt của định lý cos, áp dụng cho tam giác vuông.

Đẳng thức lượng giác của định lý Pythagoras

Trong tam giác vuông với hai cạnh kề là a và b, cùng với cạnh huyền c, ta có thể xác định giá trị sin và cos của góc θ giữa cạnh a và cạnh huyền như sau:

Kết quả từ đó là:

Kết luận cuối cùng là áp dụng định lý Pythagoras. Mối liên hệ giữa sin và cos thường được gọi là đồng nhất thức lượng giác cơ bản của định lý Pythagoras. Trong các tam giác đồng dạng, tỉ lệ giữa các cạnh luôn giống nhau, bất kể kích thước của tam giác, và tỉ lệ chỉ phụ thuộc vào góc giữa chúng. Do đó, trong hình vẽ, tam giác có cạnh huyền bằng đơn vị thì các cạnh kề sẽ là sin θ và cos θ tính theo đơn vị của cạnh huyền.

Liên quan đến tích vectơ

Định lý Pythagoras cũng kết nối tích vectơ (hay tích trực tiếp) và tích vô hướng theo cách tương tự:

$\Vert <!--\; \Vert \; -->a\times <!--\; \times \; -->b{\Vert <!--\; \Vert \; -->}^2+(a\cdot <!--\; \cdot \; -->b{)}^2=\Vert <!--\; \Vert \; -->a{\Vert <!--\; \Vert \; -->}^2\Vert <!--\; \Vert \; -->b{\Vert <!--\; \Vert \; -->}^2.$

Kết quả này có thể được nhận ra từ định nghĩa của tích trực tiếp và tích vô hướng

Trong đó, n là vectơ pháp tuyến đơn vị của cả a và b. Mối liên hệ này phù hợp với các định nghĩa và kết quả từ định lý Pythagoras.

Mối liên hệ này cũng có thể được sử dụng để định nghĩa tích trực tiếp. Khi sắp xếp lại, chúng ta thu được phương trình

$\Vert <!--\; \Vert \; -->a\times <!--\; \times \; -->b{\Vert <!--\; \Vert \; -->}^2=\Vert <!--\; \Vert \; -->a{\Vert <!--\; \Vert \; -->}^2\Vert <!--\; \Vert \; -->b{\Vert <!--\; \Vert \; -->}^2-<!--\; -\; -->(a\cdot <!--\; \cdot \; -->b{)}^2.$

Phương trình này có thể được coi là điều kiện để xác định tích trực tiếp, cũng như định nghĩa của nó, ví dụ trong không gian bảy chiều.

Mở rộng khái niệm

Các hình đồng dạng trên ba cạnh của tam giác

Nhà toán học Hippocrates của Chios vào thế kỷ V TCN đã mở rộng định lý Pythagoras, không chỉ áp dụng cho các hình vuông trên ba cạnh của tam giác mà còn cho các đa giác đồng dạng. Điều này đã được Euclid đưa vào trong cuốn Cơ sở:

Khi dựng các hình đồng dạng (theo hình học Euclid) trên các cạnh của một tam giác vuông, tổng diện tích của hai hình trên hai cạnh kề sẽ bằng diện tích của hình dựng trên cạnh huyền.

Sự mở rộng này giả định rằng các cạnh của tam giác ban đầu tương ứng với các cạnh của ba hình đồng dạng (với tỷ lệ chung giữa các cạnh là a:b). Trong khi chứng minh của Euclid chỉ áp dụng cho các đa giác lồi, định lý này cũng đúng với các đa giác lõm và cả các hình đồng dạng có biên cong (miễn là một cạnh bằng cạnh của tam giác vuông ban đầu).

Ý tưởng cốt lõi của sự mở rộng này là diện tích của một hình phẳng tỷ lệ với bình phương của bất kỳ độ dài nào, đặc biệt là tỷ lệ với bình phương của độ dài các cạnh của tam giác. Do đó, nếu dựng các hình đồng dạng với diện tích lần lượt là A, B, và C trên các cạnh của tam giác vuông a, b, và c, thì:

Theo định lý Pythagoras, a + b = c, nên A + B = C.

Ngược lại, nếu có thể chứng minh rằng A + B = C cho ba hình đồng dạng mà không cần sử dụng định lý Pythagoras, thì có thể sử dụng chứng minh đó để chứng minh định lý Pythagoras. Ví dụ, ta có thể dựng lại tam giác vuông ở trung tâm, đặt tam giác C lên cạnh huyền, và hai tam giác (A và B) dựng trên hai cạnh kề, bằng cách chia tam giác trung tâm bằng đường cao từ đỉnh góc vuông. Tổng diện tích của hai tam giác đồng dạng nhỏ sẽ bằng diện tích tam giác thứ ba, tức là A + B = C, và ngược lại điều này dẫn đến định lý Pythagoras a + b = c.

Định lý cosine

Định lý Pythagoras là một trường hợp đặc biệt của định lý tổng quát hơn liên quan đến các cạnh của một tam giác bất kỳ, được gọi là định lý cos:

$a^2+b^2-<!--\; -\; -->2ab\cos <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}=c^2,$

với θ là góc tạo bởi hai cạnh a và b.

Khi θ bằng 90 độ (π/2 radian), thì cosθ = 0, và công thức trở thành công thức Pythagoras.

Tam giác tùy ý

Xét một tam giác tùy ý với ba cạnh a, b, c, chọn một đỉnh của tam giác, và dựng một cạnh đối diện sao cho thu được một tam giác cân có góc cân bằng góc θ của đỉnh đã chọn. Giả sử góc θ chọn nằm đối diện với cạnh có độ dài c. Quy trình dựng như sau: dựng tam giác ABD với điểm D nằm trên cạnh BC, có góc ADB bằng θ và cạnh BD bằng r. Tương tự, dựng một tam giác thứ hai với góc θ đối diện cạnh b và độ dài cạnh s dọc cạnh c, như minh họa trong hình bên. Nhà toán học trung cổ Thābit ibn Qurra phát hiện rằng các cạnh của những tam giác này có mối liên hệ như sau:

$a^2+b^2=c(r+s)$

Khi góc θ tiến gần đến π/2, cạnh của tam giác cân sẽ thu hẹp lại, và độ dài r và s sẽ ít chồng lên nhau hơn. Khi θ = π/2, tam giác ADB trở thành tam giác vuông, và r + s = c, dẫn đến định lý trở về định lý Pythagoras.

Việc chứng minh định lý này khá đơn giản. Vì tam giác ABC và ABD có hai góc giống nhau, một góc chung tại đỉnh B, và hai góc bằng θ, nên tam giác ABC đồng dạng với tam giác ABD. Xét tỷ số giữa hai cạnh kề góc θ và cạnh chung của hai tam giác,

Áp dụng tương tự cho tam giác còn lại, ta có

Thực hiện biến đổi hai tỷ số trên và cộng chúng lại,

$cr+cs=a^2+b^2$

Vậy ta đã chứng minh được điều cần chứng minh.

Định lý này vẫn áp dụng cho tam giác có góc tù $\mathrm{\theta <!--\; \theta \; -->}$, khi đó hai đoạn r và s không bị chồng lên nhau.

Tam giác bất kỳ và các hình bình hành dựng trên các cạnh

Định lý diện tích Pappus là một cách mở rộng khác, áp dụng cho bất kỳ tam giác nào, thông qua việc dựng các hình bình hành trên ba cạnh của tam giác (với hình vuông là trường hợp đặc biệt khi tam giác là tam giác vuông và hình bình hành trở thành hình vuông). Hình minh họa bên phải cho thấy cách dựng các hình bình hành: Đầu tiên, dựng hai hình bình hành bất kỳ trên hai cạnh của tam giác, sau đó dựng hình bình hành thứ ba (với hai cạnh ngoài cùng của hai hình bình hành cắt nhau tại một điểm, và dựng hình bình hành thứ ba có cạnh bằng độ dài của mũi tên màu đen). Định lý cho rằng diện tích của hình bình hành thứ ba bằng tổng diện tích của hai hình bình hành ban đầu. Việc thay thế hình vuông bằng hình bình hành tạo ra sự tương đồng rất gần gũi với định lý Pythagoras gốc. Định lý này được đặt tên theo nhà toán học Pappus của Alexandria sống vào thế kỷ IV sau Công Nguyên.

Hình minh họa dưới đây mô tả cách chứng minh định lý này. Trước tiên, hãy tập trung vào hình bình hành bên trái. Hình bình hành màu lục có diện tích bằng diện tích của hình bình hành màu lam do cùng có cạnh đáy b và chiều cao h. Đồng thời, hình bình hành màu lục cũng giống như hình bình hành đầu tiên ở trên, vì chúng cùng có cạnh đáy (là cạnh của tam giác) và cùng chiều cao. Lặp lại lập luận tương tự cho hình bình hành bên phải, sau đó cộng các diện tích lại để hoàn tất chứng minh.

Hình học không gian

Trong không gian hình học, định lý Pythagoras được áp dụng như sau: Xem một hình hộp chữ nhật như hình minh họa. Theo định lý Pythagoras, đường chéo BD có giá trị là:

${\stackrel{¯<!--\; ¯\; -->}{BD}}^2={\stackrel{¯<!--\; ¯\; -->}{BC}}^2+{\stackrel{¯<!--\; ¯\; -->}{CD}}^2$

vì ba cạnh này tạo thành tam giác vuông BCD. Sử dụng đường chéo BD và cạnh đứng AB trong tam giác vuông ABD, ta có thể tính được chiều dài đường chéo AD bằng cách áp dụng định lý Pythagoras thêm một lần nữa:

${\stackrel{¯<!--\; ¯\; -->}{AD}}^2={\stackrel{¯<!--\; ¯\; -->}{AB}}^2+{\stackrel{¯<!--\; ¯\; -->}{BD}}^2$

và kết hợp với kết quả trước đó để có:

${\stackrel{¯<!--\; ¯\; -->}{AD}}^2={\stackrel{¯<!--\; ¯\; -->}{AB}}^2+{\stackrel{¯<!--\; ¯\; -->}{BC}}^2+{\stackrel{¯<!--\; ¯\; -->}{CD}}^2$

Kết quả này cho thấy độ lớn của vectơ v (đường chéo AD) được biểu diễn qua các thành phần trực giao của nó {v_k} (dưới đây là ba thành phần trực giao):

$\Vert <!--\; \Vert \; -->v{\Vert <!--\; \Vert \; -->}^2=\underset{k=1}{\overset{3}{\sum <!--\; \sum \; -->}}\Vert <!--\; \Vert \; -->v_k{\Vert <!--\; \Vert \; -->}^2.$

Dựa vào công thức trên, chúng ta có thể xem đây là một phiên bản tổng quát của định lý Pythagoras cho không gian nhiều chiều. Tuy nhiên, kết quả này thực chất là sự áp dụng lại của định lý Pythagoras cho các tam giác vuông trong các mặt phẳng trực giao.

Một phiên bản mở rộng của định lý Pythagoras trong không gian ba chiều là định lý de Gua, được đặt theo tên Jean Paul de Gua de Malves: Nếu một tứ diện có một góc khối vuông (giống như góc của một hình lập phương), thì bình phương diện tích của mặt đối diện với góc khối vuông bằng tổng bình phương diện tích của ba mặt còn lại. Điều này có thể được mở rộng cho 'định lý Pythagoras n chiều':

Giả sử $x_1,x_2,\dots <!--\; \dots \; -->,x_n$ là các vectơ trực giao trong ℝ. Xem xét một đơn hình n chiều S với các đỉnh $0,x_1,\dots <!--\; \dots \; -->,x_n$. (Xem đơn hình (n − 1) chiều với các đỉnh $x_1,\dots <!--\; \dots \; -->,x_n$ không bao gồm gốc như là 'cạnh huyền' của S và phần còn lại các mặt (n − 1) chiều S như là các 'chân' của nó.) Khi đó, bình phương thể tích của 'cạnh huyền' của S bằng tổng bình phương thể tích của n chân của nó.

Nhận định này được minh họa trong không gian ba chiều bằng tứ diện như trong hình. 'Cạnh huyền' chính là mặt đáy của tứ diện nằm ở mặt sau của hình, và 'các chân' là ba mặt xuất phát từ đỉnh của góc khối vuông. Khi chiều cao từ đỉnh xuống mặt đáy thay đổi, diện tích của ba mặt bên cũng thay đổi, trong khi mặt đáy giữ nguyên. Định lý gợi ý rằng khi chiều cao đạt giá trị phù hợp tạo ra góc vuông ở đỉnh thì định lý Pythagoras tổng quát có thể được áp dụng. Diễn đạt theo cách khác:

Cho một đơn hình n-hộp chữ nhật trong không gian n chiều, bình phương của diện tích của mặt đối diện với góc vuông sẽ bằng tổng bình phương của diện tích của các mặt còn lại trong cùng không gian.

Không gian tích trong

Định lý Pythagoras có thể được mở rộng trong không gian tích trong, khái niệm này là sự tổng quát của không gian Euclid hai và ba chiều. Ví dụ, một hàm số có thể được coi là một vectơ với các thành phần vô hạn trong không gian tích trong, như trong giải tích hàm.

Trong không gian tích trong, khái niệm vuông góc được thay thế bằng khái niệm trực giao: hai vectơ v và w được coi là trực giao nếu tích trong $⟨<!--\; ⟨\; -->v,w⟩<!--\; ⟩\; -->$ bằng không. Tích trong là một dạng tổng quát của tích vô hướng vectơ. Tích vô hướng thường được gọi là tích trong tiêu chuẩn hay tích trong Euclid, tuy nhiên có thể định nghĩa nhiều loại tích trong khác nhau.

Khái niệm độ dài được thay thế bằng chuẩn ||v|| của một vectơ v, được định nghĩa như sau:

$\Vert <!--\; \Vert \; -->v\Vert <!--\; \Vert \; -->\equiv <!--\; \equiv \; -->\sqrt{⟨<!--\; ⟨\; -->v,v⟩<!--\; ⟩\; -->}.$

Trong không gian tích trong, định lý Pythagoras khẳng định rằng đối với hai vectơ trực giao bất kỳ v và w có

${\Vert v+w\Vert }^2={\Vert v\Vert }^2+{\Vert w\Vert }^2.$

Tại đây, các vectơ v và w có thể được xem như là hai cạnh kề của một tam giác vuông, với cạnh huyền được xác định bởi phép cộng vectơ v + w. Dạng của định lý Pythagoras này là một hệ quả từ các tính chất của không gian tích trong:

${\Vert v+w\Vert }^2=⟨<!--\; ⟨\; -->v+w,v+w⟩<!--\; ⟩\; -->=⟨<!--\; ⟨\; -->v,v⟩<!--\; ⟩\; -->+⟨<!--\; ⟨\; -->w,w⟩<!--\; ⟩\; -->+⟨<!--\; ⟨\; -->v,w⟩<!--\; ⟩\; -->+⟨<!--\; ⟨\; -->w,v⟩<!--\; ⟩\; -->={\Vert v\Vert }^2+{\Vert w\Vert }^2,$

với tích trong của các số hạng chéo bằng không, vì chúng là trực giao với nhau.

Định lý Pythagoras có thể được mở rộng trong không gian tích trong, không chỉ áp dụng cho các vectơ trực giao mà còn liên quan đến định lý hình bình hành:

$2\Vert <!--\; \Vert \; -->v{\Vert <!--\; \Vert \; -->}^2+2\Vert <!--\; \Vert \; -->w{\Vert <!--\; \Vert \; -->}^2=\Vert <!--\; \Vert \; -->v+w{\Vert <!--\; \Vert \; -->}^2+\Vert <!--\; \Vert \; -->v-<!--\; -\; -->w{\Vert <!--\; \Vert \; -->}^2$

Điều này chứng tỏ rằng gấp đôi tổng bình phương độ dài các cạnh của hình bình hành chính là tổng bình phương độ dài của các đường chéo của nó. Bất kỳ chuẩn nào thỏa mãn phương trình này đều là chuẩn trong không gian tích trong.

Định lý Pythagoras cũng có thể áp dụng cho nhiều vectơ trực giao hơn hai. Nếu v₁, v₂,..., v_n là các vectơ trực giao trong không gian tích trong, thì khi áp dụng định lý Pythagoras liên tiếp cho từng cặp vectơ này (giống như với các cạnh của hình hộp chữ nhật trong hình học không gian), ta có phương trình sau:

${\Vert \underset{k=1}{\overset{n}{\sum <!--\; \sum \; -->}}{v}_k\Vert }^2=\underset{k=1}{\overset{n}{\sum <!--\; \sum \; -->}}\Vert <!--\; \Vert \; -->v_k{\Vert <!--\; \Vert \; -->}^2$

Hình học không Euclid

Định lý Pythagoras xuất phát từ các tiên đề của hình học Euclid, và thực tế, nó không áp dụng trong hình học không Euclid. (Có thể chứng minh rằng định lý Pythagoras tương đương với tiên đề về đường thẳng song song của Euclid - tiên đề thứ năm). Nói cách khác, trong hình học không Euclid, mối liên hệ giữa các cạnh của một tam giác không còn tuân theo công thức Pythagoras. Ví dụ, trong hình học cầu, các cạnh của một tam giác vuông (là a, b, và c) chiếm một phần tám của mặt cầu đơn vị với chiều dài bằng nhau là π/2, và tất cả các góc đều là góc vuông, hoặc không tuân theo định lý Pythagoras vì a + b ≠ c.

Chúng ta xem xét hai loại hình học không Euclid là hình học cầu và hình học hyperbolic; trong mỗi trường hợp, tương tự như hình học Euclid đối với tam giác không vuông, công thức Pythagoras được thay thế bằng định lý cos phù hợp.

Tuy nhiên, định lý Pythagoras vẫn áp dụng trong hình học hyperbolic và hình học elliptic nếu điều kiện tam giác vuông được thay bằng điều kiện tổng của hai góc bằng góc còn lại, như A+B = C. Khi đó, ba cạnh có mối liên hệ như sau: tổng diện tích của hai hình tròn với đường kính a và b bằng diện tích của hình tròn có đường kính c.

Hình học cầu

Đối với bất kỳ tam giác vuông nào trên mặt cầu có bán kính R (chẳng hạn, nếu γ trong hình là góc vuông), với các cạnh là a, b, và c, các cạnh này liên hệ theo công thức sau:

$\cos <!--\; \; -->\left(\frac{c}{R}\right)=\cos <!--\; \; -->\left(\frac{a}{R}\right)\cos <!--\; \; -->\left(\frac{b}{R}\right).$

Công thức này là một trường hợp đặc biệt của định lý cos trên mặt cầu, áp dụng cho tất cả các tam giác trên mặt cầu:

$\cos <!--\; \; -->\left(\frac{c}{R}\right)=\cos <!--\; \; -->\left(\frac{a}{R}\right)\cos <!--\; \; -->\left(\frac{b}{R}\right)+\sin <!--\; \; -->\left(\frac{a}{R}\right)\sin <!--\; \; -->\left(\frac{b}{R}\right)\cos <!--\; \; -->\mathrm{\gamma <!--\; \gamma \; -->}$

Thông qua việc sử dụng chuỗi Maclaurin cho hàm cos với khai triển tiệm cận và ký hiệu O lớn cho số hạng còn lại,

$\cos <!--\; \; -->x=1-<!--\; -\; -->\frac{x^2}{2}+O\left(x^4\right)\text{ khi }x\to <!--\; \to \; -->0$

Khi bán kính R trở nên rất lớn và các đối số a/R, b/R, và c/R tiến gần về 0, thì công thức liên hệ giữa các cạnh của tam giác vuông trên mặt cầu sẽ gần giống như công thức Pythagoras trong hình học Euclid. Thay thế khai triển tiệm cận vào từng hàm cos trong công thức tam giác cầu, ta có được

$1-<!--\; -\; -->\frac{1}{2}{\left(\frac{c}{R}\right)}^2+O\left(\frac{1}{R^4}\right)=\left[1-<!--\; -\; -->\frac{1}{2}{\left(\frac{a}{R}\right)}^2+O\left(\frac{1}{R^4}\right)\right]\left[1-<!--\; -\; -->\frac{1}{2}{\left(\frac{b}{R}\right)}^2+O\left(\frac{1}{R^4}\right)\right]\text{ khi }R\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}$

Do các hằng số a, b, và c không phụ thuộc vào bán kính R, chúng được gộp vào số hạng O lớn còn lại. Liên hệ tiệm cận này có thể được đơn giản hóa thêm bằng cách thực hiện khai triển tích đã nêu, loại bỏ các số hạng không cần thiết, nhân hai vế với −2 và sắp xếp lại các số hạng.

${\left(\frac{c}{R}\right)}^2={\left(\frac{a}{R}\right)}^2+{\left(\frac{b}{R}\right)}^2+O\left(\frac{1}{R^4}\right)\text{ khi }R\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}$

Sau khi nhân với R, ta thu được công thức Pythagoras trong hình học Euclid: c = a + b khi bán kính R trở nên vô hạn lớn (vì các số hạng khác trở nên không đáng kể):

$c^2=a^2+b^2+O\left(\frac{1}{R^2}\right)\text{ khi }R\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}$

Đối với một tam giác nhỏ với các cạnh a, b đều nhỏ hơn nhiều so với R, có thể bỏ qua hàm cos để tránh hiện tượng mất ý nghĩa (loss of significance), và thu được:

${\sin }^2<!--\; \; -->\frac{c}{2R}={\sin }^2<!--\; \; -->\frac{a}{2R}+{\sin }^2<!--\; \; -->\frac{b}{2R}-<!--\; -\; -->2{\sin }^2<!--\; \; -->\frac{a}{2R}{\sin }^2<!--\; \; -->\frac{b}{2R}.$

Hình học hyperbolic

Trong không gian hyperbolic với độ cong đều −1/R, tam giác vuông có hai cạnh kề là a, b và cạnh huyền là c, có mối quan hệ giữa các cạnh như sau:

$\cosh <!--\; \; -->\frac{c}{R}=\cosh <!--\; \; -->\frac{a}{R}\cosh <!--\; \; -->\frac{b}{R}$

Hàm cosh là hàm cos hyperbolic. Công thức này là một dạng đặc biệt của định lý cos hyperbolic áp dụng cho mọi tam giác trong không gian hyperbolic.

$\cosh <!--\; \; -->\frac{c}{R}=\cosh <!--\; \; -->\frac{a}{R}\cosh <!--\; \; -->\frac{b}{R}-<!--\; -\; -->\sinh <!--\; \; -->\frac{a}{R}\sinh <!--\; \; -->\frac{b}{R}\cos <!--\; \; -->\mathrm{\gamma <!--\; \gamma \; -->}$

Trong đó γ là góc đối diện với cạnh c.

Sử dụng chuỗi Maclaurin cho hàm cos hyperbolic, cosh x ≈ 1 + x/2, có thể chứng minh rằng khi tam giác hyperbolic trở nên cực kỳ nhỏ (tức là, khi a, b, và c gần bằng zero), liên hệ hyperbolic cho tam giác vuông gần giống như định lý Pythagoras.

Đối với một tam giác vuông rất nhỏ (a, b << R), hàm sinh hyperbolic có thể được viết theo cách sau mà không mất độ chính xác đáng kể

${\sinh }^2<!--\; \; -->\frac{c}{2R}={\sinh }^2<!--\; \; -->\frac{a}{2R}+{\sinh }^2<!--\; \; -->\frac{b}{2R}+2{\sinh }^2<!--\; \; -->\frac{a}{2R}{\sinh }^2<!--\; \; -->\frac{b}{2R}.$

Tam giác cực kỳ nhỏ

Dành cho mọi độ cong K (có thể là dương, bằng 0, hoặc âm), trong một tam giác cực kỳ nhỏ (với |K|a, |K|b << 1) và cạnh huyền là c, có thể chứng minh được mối liên hệ như sau:

Hình học vi phân

Trong không gian ba chiều, định lý Pythagoras mô tả khoảng cách giữa hai điểm rất gần nhau:

$d{s}^2=d{x}^2+d{y}^2+d{z}^2,$

Trong đó, ds là yếu tố khoảng cách và (dx, dy, dz) là các thành phần của vectơ nối hai điểm. Những không gian như vậy được gọi là không gian Euclid. Tuy nhiên, trong hình học Riemann, công thức tổng quát áp dụng cho mọi hệ tọa độ toàn cục và không gian tổng quát có dạng:

$d{s}^2=\underset{i,j}{\overset{n}{\sum <!--\; \sum \; -->}}{g}_{ij}d{x}_{i}d{x}_j$

Mà các nhà toán học thường gọi là tensor metric. (Đôi khi thuật ngữ này được dùng để chỉ tập hợp các hệ số g_ij.) Đây là một hàm số phụ thuộc vào vị trí và dùng để mô tả các không gian cong. Ví dụ đơn giản là khoảng cách trong không gian phẳng (không gian Euclid) được diễn tả trong hệ tọa độ cong, như trong hệ tọa độ cực:

$d{s}^2=d{r}^2+r^{2}d{\mathrm{\theta <!--\; \theta \; -->}}^2$

Trong không-thời gian phẳng theo thuyết tương đối hẹp, tenxơ mêtric Minkowski được biểu diễn như sau:

$\mathrm{\Delta <!--\; \Delta \; -->}{s}^2=-<!--\; -\; -->c^2\mathrm{\Delta <!--\; \Delta \; -->}{t}^2+\mathrm{\Delta <!--\; \Delta \; -->}{x}^2+\mathrm{\Delta <!--\; \Delta \; -->}{y}^2+\mathrm{\Delta <!--\; \Delta \; -->}{z}^2=d{s}^2=-<!--\; -\; -->c^{2}d{t}^2+d{x}^2+d{y}^2+d{z}^2={\mathrm{\eta <!--\; \eta \; -->}}_{\mathrm{\mu <!--\; \mu \; -->}\mathrm{\nu <!--\; \nu \; -->}}d{x}^{\mathrm{\mu <!--\; \mu \; -->}}d{x}^{\mathrm{\nu <!--\; \nu \; -->}}$

Trong không-thời gian cong theo thuyết tương đối rộng, tenxơ mêtric là giải của phương trình trường Einstein và các điều kiện biên, ví dụ điển hình là mêtric Schwarzschild trong hệ tọa độ cầu $x^{\mathrm{\mu <!--\; \mu \; -->}}\to <!--\; \to \; -->(ct,r,\mathrm{\theta <!--\; \theta \; -->},\mathrm{\varphi <!--\; \varphi \; -->})$ với hệ số mêtric (-, +, +, +):

$d{s}^2=c^2{d\mathrm{\tau <!--\; \tau \; -->}}^2=-<!--\; -\; -->\left(1-<!--\; -\; -->\frac{r_s}{r}\right)c^2+\left(\mathrm{r}+rsin\mathrm{\theta <!--\; \theta \; -->})\right)+\left(rsin\mathrm{\theta <!--\; \theta \; -->})\right)d^{\mathrm{\theta <!--\; \theta \; -->}}=d^r+-<!--\; -\; -->r^{2}d{\mathrm{\theta <!--\; \theta \; -->}}^2$

Lịch sử

Có nhiều tranh cãi về việc định lý Pythagoras được phát hiện một lần duy nhất hay nhiều lần ở các nền văn hóa khác nhau, và ngày phát hiện cùng thời điểm chứng minh đầu tiên không được xác định rõ. Nhà sử học toán học Joran Friberg cho rằng các nhà toán học của triều đại Babylon thứ nhất (khoảng thế kỷ XX đến thế kỷ XVI TCN) đã biết đến định lý này, sớm hơn 1000 năm trước khi Pythagoras xuất hiện. Do đó, nhà thống kê học Stephen Stigler đã đưa ra định luật rằng không có khám phá khoa học nào được đặt tên theo người đầu tiên phát hiện ra nó (định luật Stigler về đặt tên khám phá khoa học). Những nguồn tài liệu khác, như sách của Leon Lederman và Dick Teresi, cho rằng Pythagoras là người đã phát hiện ra định lý, mặc dù Teresi sau đó cho biết người Babylon đã phát triển định lý này ít nhất mười lăm thế kỷ trước khi Pythagoras sinh ra. Có thể chia lịch sử định lý Pythagoras thành bốn giai đoạn: khám phá và hiểu biết về bộ ba số Pythagoras, hiểu về mối quan hệ giữa các cạnh của tam giác vuông, hiểu mối quan hệ giữa các cạnh chung một góc trong tam giác, và chứng minh định lý dựa trên phương pháp suy diễn từ hệ tiên đề.

Bartel Leendert van der Waerden (1903–1996) đã giả thuyết rằng các nhà toán học Babylon đã phát hiện bộ ba Pythagoras bằng phương pháp đại số. Vào khoảng năm 2000 và 1786 TCN, trong 'cuộn giấy cói Berlin 6619' của Trung Vương quốc Ai Cập có chứa một bài toán có nghiệm là bộ ba số Pythagoras 6:8:10, mặc dù bài toán này không liên quan đến tam giác vuông. Phiến đất sét Lưỡng Hà Plimpton 322, được viết trong khoảng thời gian từ 1790 đến 1750 TCN dưới triều đại vua Hammurabi, chứa nhiều đoạn mô tả có liên hệ mật thiết với bộ ba số Pythagoras.

Tại Ấn Độ, đoạn kinh Sulba Sutra Baudhayana, từ khoảng giữa thế kỷ VIII đến V TCN, liệt kê các bộ ba số Pythagoras được phát hiện bằng phương pháp đại số, đưa ra phát biểu về định lý Pythagoras, và chứng minh định lý này bằng phương pháp hình học đối với trường hợp tam giác vuông cân. Đoạn kinh Sutra Sulba Apastamba (khoảng năm 600 TCN) cung cấp phương pháp chứng minh định lý Pythagoras bằng số đối với bất kỳ tam giác vuông nào, sử dụng tính diện tích hình học. Van der Waerden cho rằng 'nó chắc chắn dựa trên các truyền thống trước đó'. Carl Boyer cho rằng định lý Pythagoras trong kinh Śulba-sũtram có thể đã bị ảnh hưởng bởi toán học của người Lưỡng Hà cổ đại, nhưng không có bằng chứng rõ ràng để xác nhận hoặc bác bỏ giả thuyết này.

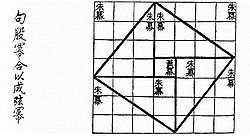
Tài liệu từ thế kỷ I TCN, quyển Chu bễ toán kinh (周髀算经) của Trung Hoa cổ đại, được phương Tây dịch là The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven, giải thích định lý Pythagoras qua bộ ba số (3, 4, 5) của tam giác vuông—ở Trung Quốc gọi là 'định lý Gougu' (勾股定理). Trong triều đại nhà Hán (202 TCN đến 220 SCN), bộ ba Pythagoras cũng xuất hiện trong Cửu chương toán thuật cùng với các tam giác vuông. Một số nhà lịch sử toán học cho rằng định lý này xuất hiện lần đầu ở Trung Quốc với tên gọi khác là 'định lý Thương Cao' (商高定理), theo tên của nhà toán học và thiên văn học thời nhà Chu, người đã cùng Chu Công Đán biên soạn Chu bễ toán kinh. Tác phẩm cũng được các học giả sau này như Lưu Huy và Lý Thuần Phong bổ sung và chỉnh sửa.

Pythagoras (khoảng 569–475 TCN) đã áp dụng phương pháp đại số để xây dựng các bộ ba số Pythagoras, theo lời bình luận của Proclus về các công trình của Euclid. Tuy nhiên, Proclus cho rằng tác phẩm được viết vào khoảng năm 410 đến 485 AD. Theo Thomas L. Heath (1861–1940), không có tài liệu cụ thể về sự tồn tại của định lý Pythagoras trong các văn bản Hy Lạp từ 5 thế kỷ sau thời của Pythagoras. Dù vậy, khi Plutarchus và Cicero ghi nhận công lao của Pythagoras đối với định lý này, họ viết như thể những đóng góp của ông đã được công nhận rộng rãi. 'Liệu công thức này có đúng thuộc về Pythagoras hay không, [...] có thể an tâm rằng nó thuộc về giai đoạn rất sớm của toán học Pythagoras.'

Khoảng năm 400 TCN, theo Proclus, Plato đã phát triển phương pháp tìm các bộ ba Pythagoras bằng cách kết hợp đại số và hình học. Vào khoảng năm 300 TCN, cuốn Cơ sở của Euclid đã ghi lại chứng minh toán học cổ xưa nhất cho định lý này.

Ứng dụng

Định lý Pythagoras giúp xác định chiều dài của một cạnh trong tam giác vuông khi đã biết độ dài của hai cạnh còn lại, mà không cần biết chu vi của tam giác.

Định lý Pythagoras có thể được sử dụng để kiểm tra xem một tam giác có phải là tam giác vuông hay không (hoặc không phải là tam giác vuông), chỉ dựa trên độ dài của ba cạnh mà không cần phải đo góc vuông.

Định lý Pythagoras chỉ áp dụng cho tam giác vuông.