Định lý

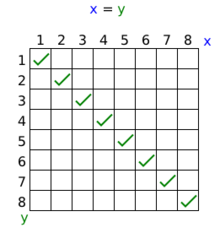
Trong toán học, định lý biểu thị mối quan hệ giữa hai đại lượng hoặc hai biểu thức, khẳng định rằng chúng có giá trị bằng nhau, tức là chúng đại diện cho cùng một đối tượng toán học. Định lý giữa $a$ và $b$ được viết là $a=b$ và đọc là $a$ bằng $b$, trong đó $a$ và $b$ là hai phần của định lý. Ví dụ:

• $x=y$ có nghĩa là $x$ và $y$ biểu thị cùng một đối tượng.
• $(x+1$
  ) 2 = x 2 + 2 x + 1 {\displaystyle (x+1)^{2}=x^{2}+2x+1} cho thấy rằng nếu $x$ là một số bất kỳ, hai biểu thức này vẫn có giá trị như nhau. Điều này cũng có thể hiểu là hai phần của định lý đại diện cho cùng một hàm số.

Nguồn gốc

Thuật ngữ 'định lý' xuất phát từ hai phần trong Hán-Việt: định ('bằng nhau') và lý ('quy tắc').

Các tính chất

Tính chất chuyển tiếp

• $a=b;b=c\Rightarrow <!--\; \Rightarrow \; -->a=c$

Tính chất liên quan đến phép cộng và phép trừ

• $a=b\Rightarrow <!--\; \Rightarrow \; -->a+c=b+c$ ($a,b\in <!--\; \in \; -->R$)
• $a=b\Rightarrow <!--\; \Rightarrow \; -->a-<!--\; -\; -->c=b-<!--\; -\; -->c$ ($a,b\in <!--\; \in \; -->R$)

Tính chất liên quan đến phép nhân và phép chia

• $a=b\Rightarrow <!--\; \Rightarrow \; -->ac=bc$ ($a,b\in <!--\; \in \; -->R$)
• $a=b\Rightarrow <!--\; \Rightarrow \; -->\frac{a}{c}=\frac{b}{c}$ ($a,b\in <!--\; \in \; -->R$)

Các khái niệm liên quan

Đối tỷ lệ

Tỷ lệ thức là một đẳng thức trong đó hai tỷ lệ (hay tỷ số) được so sánh với nhau, được biểu diễn bằng công thức A:B = C:D hoặc dưới dạng phân số như {A/B = C/D}.

Trong một tỷ lệ thức {A/B = C/D}, các số A và D gọi là các số hạng ngoài hay ngoại tỷ, còn B và C là các số hạng trong hay trung tỷ. Việc hoán đổi các số hạng ngoài và trong hoặc nghịch đảo tỷ lệ thức ban đầu sẽ tạo ra các tỷ lệ thức mới.

• {D/B = C/A}
• {A/C = B/D}
• {B/A = D/C}

Nếu nhân các số hạng ngoài và các số hạng trong của tỷ lệ thức, chúng ta có được đẳng thức: {A × D = B × C}.

Khi ba hay nhiều tỷ lệ được nối với nhau bằng dấu '=' như A:B = C:D = E:F, chúng tạo thành một dãy tỷ lệ thức hay còn gọi là dãy tỉ lệ thức.

Đồng nhất thức

Khi a và b đều là các hàm số, thì a = b cho thấy a và b là những hàm số giống hệt nhau. Một đẳng thức như vậy giữa các hàm số thường được gọi là đồng nhất thức. Ví dụ: (y + 1)² = y² + 2y + 1. Đôi khi, đồng nhất thức cũng được viết dưới dạng: (y + 1)² ≡ y² + 2y + 1.

Phương trình

Phương trình là bài toán tìm giá trị cho một hoặc nhiều biến số, gọi là ẩn số, sao cho đẳng thức trong phương trình được thỏa mãn.

• Bất đẳng thức
• Bảy hằng đẳng thức quan trọng

Tài liệu tham khảo

Các liên kết hữu ích

• Hazewinkel, Michiel (biên tập) (2001). “Equality axioms”, Bách khoa toàn thư Toán học, Springer. ISBN 978-1-55608-010-4