Định nghĩa, tính chất và dấu hiệu nhận biết Hình thoi và các bài tập liên quan Lý thuyết và bài tập Hình thoi lớp 8

Để hỗ trợ học sinh lớp 8, Mytour giới thiệu Chuyên đề Hình thoi. Tài liệu này tổng hợp kiến thức lý thuyết như: định nghĩa, tính chất, dấu hiệu nhận biết và bài tập về hình thoi. Dưới đây là nội dung chi tiết, mời các bạn tham khảo và tải tài liệu tại đây.

Tổng hợp Lý thuyết về Hình thoi

Định nghĩa của Hình thoi

Tính chất cơ bản của Hình thoi

Hình thoi là một loại hình có

• Các góc đối diện bằng nhau.
• Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
• Hai đường chéo chia các góc trong hình thoi thành 2 góc bằng nhau (đường phân giác).
• Hình thoi có tất cả các tính chất của hình bình hành.

Dấu hiệu nhận biết Hình thoi

Hình thoi là một loại hình tứ giác đặc biệt

• Tứ giác có bốn cạnh bằng nhau là hình thoi.
• Tứ giác có hai đường chéo là đường phân giác của cả bốn góc là hình thoi.
• Tứ giác có hai đường chéo là đường trung trực của nhau là hình thoi.

Hình thoi là một dạng đặc biệt của Hình bình hành

Do hình thoi là một biến thể đặc biệt của hình bình hành, nên nó sẽ có tất cả các đặc tính của hình bình hành cùng với một số đặc tính bổ sung như:

• Hình bình hành có hai cạnh bên bằng nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

Ví dụ minh họa

Ví dụ số 1:

Cho hình thoi ABCD, mỗi cạnh đều dài 13cm. Gọi O là điểm giao của hai đường chéo. Vẽ đoạn OH vuông góc với AD. Biết OH = 6cm, tính tỉ số của đường chéo BD và AC.

Giải bài toán

* Phương pháp giải quyết

Vẽ thêm đoạn BK vuông góc với AD để áp dụng định lý về đường trung trực trong tam giác, định lý Pythagoras để tính bình phương của độ dài từng đoạn đường chéo.

* Bước giải chi tiết

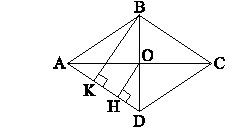
Vẽ đoạn BK vuông góc với AD.

Xét tam giác DBKD có OH // BK (do cùng vuông góc với AD) và OB = OD nên KH = HD.

Do đó OH là đường trung bình của tam giác DBKD.

Kết luận được BK = 12cm.

Xét tam giác DABK vuông tại K có AK² = AB² – BK² = 13² – 12² = 25 ⇒ AK = 5cm, do đó KD = 8cm.

Xét tam giác DBKD vuông tại K có BD² = BK² + KD² = 12² + 8² = 208.

Xét tam giác DAOH vuông tại H có OA² = OH² + AH² = 6² + 9² = 117.

Ví dụ số 2:

Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đoạn thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G lên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.

*Phương pháp giải quyết

Sử dụng định lý về đường trung trực trong tam giác, ta chứng minh được tứ giác DNGM là hình bình hành. Sau đó, chứng minh hai cạnh kề bằng nhau.

*Bước giải chi tiết

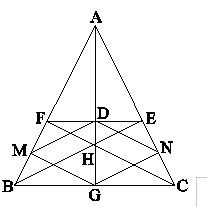
DABE = DACF (đối diện nhau, góc nhọn)

⇒ AE = AF và BE = CF.

Vì H là trực tâm của tam giác DABC, nên AH là đường cao, đồng thời cũng là đường trung tuyến, từ đó GB = GC và DE = DF.

Do H là trực tâm của tam giác DABC, nên AH là đường cao, cũng là đường trung trực, từ đó GB = GC và DE = DF.

Xét tam giác DEBC có GN // BE (cùng vuông góc với AC) và GB = GC nên NE = NC.

Chứng minh tương tự, ta có MF = MB.

Áp dụng định lý về đường trung trực trong tam giác, ta chứng minh được DM // GN và DM = GN nên tứ giác DNGM là hình bình hành.

Bài tập Ôn tập về Hình thoi

Bài 1. Một hình thoi có một góc nhọn là 30^o. Khoảng cách từ giao điểm của hai đường chéo đến mỗi cạnh là h. Hãy tính độ dài mỗi cạnh của hình thoi.

Bài 2. Cho hình thoi ABCD có chu vi bằng 8cm. Tìm giá trị lớn nhất của tích của hai đường chéo.

Bài 3. Trong hình thoi ABCD, góc A đo 40 độ. Gọi M là trung điểm của AB. Vẽ đoạn DH vuông góc với đoạn CM. Hãy tính số đo của góc MHB.

Bài 4. Cho hình thoi ABCD. Trên nửa mặt phẳng chứa đoạn BD mà có C là trên đó, hãy vẽ hình bình hành BDEF có độ dài DE bằng DC. Chứng minh rằng C là trực tâm của tam giác AEF.

............

Tải tài liệu để biết thêm thông tin chi tiết