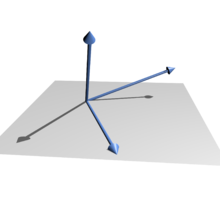
 Các vectơ độc lập tuyến tính trong không gian ba chiều.
Các vectơ độc lập tuyến tính trong không gian ba chiều. Các vectơ phụ thuộc tuyến tính trên một mặt phẳng trong không gian ba chiều.
Các vectơ phụ thuộc tuyến tính trên một mặt phẳng trong không gian ba chiều.
Trong đại số tuyến tính, độc lập tuyến tính là một thuộc tính chỉ sự liên hệ giữa các vectơ.
Độc lập tuyến tính và phụ thuộc tuyến tính
- Một tập hợp các vectơ {v1,...,vn} trong không gian vectơ V được gọi là phụ thuộc tuyến tính,
nếu có tồn tại các số: k1,..., kn không đồng thời bằng 0 sao cho:
- k1 v1 +... + kn vn = 0.
- tập hợp các vectơ là độc lập tuyến tính khi và chỉ khi phương trình vectơ:
- k1 v1 +... + kn vn = 0
chỉ có duy nhất một nghiệm: k1 = k2 =... = kn = 0
Đặc tính
Cho V là một không gian vector trên trường K:
| Phụ thuộc tuyến tính | Độc lập tuyến tính |
|---|---|
| Mọi tập hợp chứa vectơ 0v đều phụ thuộc tuyến tính, tức là nếu 0v ∈ S thì S phụ thuộc tuyến tính. | Mọi tập hợp độc lập tuyến tính thì không chứa vectơ 0v, tức là nếu S là tập con độc lập tuyến tính của V thì 0vS. |
| Mọi tập hợp chứa tập con phụ thuộc tuyến tính thì nó phụ thuộc tuyến tính, tức là nếu E F và E phụ thuộc tuyến tính thì F phụ thuộc tuyến tính. | Mọi tập con khác rỗng của một tập độc lập tuyến tính thì độc lập tuyến tính. Tức là ≠ E F và F độc lập tuyến tính thì E độc lập tuyến tính. |
| Tập S={u1,u2,...,um} (m≥2) phụ thuộc tuyến tính khi và chỉ khi tồn tại vectơ ui ∈ S sao cho ui là tổ hợp tuyến tính của các vectơ còn lại trong S. | Tập S ≠ độc lập tuyến tính khi và chỉ khi mỗi vectơ bất kỳ u ∈ S đầu không thể là tổ hợp tuyến tính của các vectơ còn lại trong S. |
| Mọi tập khác rỗng S V thì hoặc S độc lập tuyến tính hoặc S phụ thuộc tuyến tính. | |
Ý nghĩa hình học
- Trong không gian các vector trên mặt phẳng, một hệ gồm hai vector được coi là độc lập tuyến tính khi và chỉ khi chúng không cùng phương.
- Trong không gian ba chiều, một hệ ba vector được coi là độc lập tuyến tính khi và chỉ khi chúng không cùng mặt phẳng.
Ví dụ minh họa
- Đối với vectơ (1,2,3,4) và (-3,-6,-9,5), chúng là độc lập tuyến tính.
- (1,2) và (-2,-4) không độc lập tuyến tính vì có tồn tại λ1 = 1 và λ2 = 2 sao cho λ1(-2,-4) + λ2(1,2) = 0.
Độc lập tuyến tính trong không gian (hoặc )
- Trong không gian R, một hệ chứa nhiều hơn n vectơ {v1,...,vm} luôn bị phụ thuộc tuyến tính.
- Nếu hệ các vectơ {v1,...,vm} là độc lập tuyến tính trong không gian R, thì tất cả các vectơ có dạng sau:
- k1 v1 +... + km vm
- là một không gian con tương đương với R.
- Một bộ n vector {v1,...,vn} là độc lập tuyến tính trong không gian R nếu và chỉ nếu ma trận được tạo thành từ các vector này có định thức khác không (det A ≠ 0).
- Một bộ n vector {v1,...,vn} là phụ thuộc tuyến tính trong không gian R nếu và chỉ nếu ma trận được tạo thành từ các vector này có định thức bằng không (det A = 0).
