Đường cong ROC

Buzz

Nội dung bài viết

Hoàn cảnh ra đời

Tính chất

Ứng dụng

Liên kết ngoài

Phần mềm

Xem thêm

Đọc tóm tắt

- Đường cong ROC là biểu đồ để xác định tín hiệu và nhiễu trong hệ thống phân loại nhị phân.
- Đường cong ROC được sử dụng rộng rãi trong nghiên cứu và ứng dụng, từ tâm lý vật lý đến y học.
- Đường cong ROC thể hiện độ chính xác của kiểm tra và khả năng phân biệt tốt hay xấu.
- Diện tích dưới đường cong ROC được sử dụng để so sánh giữa các phép kiểm tra và đánh giá hiệu quả của chúng.
- Đường cong ROC cũng được sử dụng để tóm tắt thống kê và đánh giá khả năng dự đoán của các thuật toán.

Trong lý thuyết phát hiện tín hiệu, đường cong ROC, tiếng Anh receiver operating characteristic (ROC), còn được gọi là receiver operating curve (đường cong đặc trưng hoạt động của bộ thu nhận - để xác định xem có tín hiệu hay chỉ là nhiễu), là một biểu đồ với trục hoành là Độ nhạy và trục tung là (1 - Đặc trưng) cho một hệ thống phân loại nhị phân khi ngưỡng phân loại thay đổi (giá trị ngưỡng nằm trên trục hoành, đường thẳng đứng biểu thị sự phân tách: phần bên trái được xem là không có thuộc tính cần kiểm tra, phần bên phải được xem là có thuộc tính cần kiểm tra) (xem hình).

Giá trị của ngưỡng sẽ quyết định số lượng: true positives, true negatives, false positives, false negatives (xem trong phân loại nhị phân).

Đường cong ROC cũng có thể được biểu diễn dưới dạng vẽ phần true positive (TP) theo phần false positive (FP).

Hiệu số (1 - Đặc trưng) bằng false positive (FP), ví dụ: đặc trưng=0,9 thì FP=0,1.
Ứng với mỗi ngưỡng, sẽ cho ta một điểm (true positive, false positive).
Vì vậy với nhiều ngưỡng khác nhau, ta sẽ có một tập hợp các điểm trên đồ thị TP-FP.
Tập hợp các điểm này sẽ tạo thành đường cong ROC.

Cách biểu diễn đường cong ROC

Hoàn cảnh ra đời

Việc sử dụng đường cong ROC cũng rất phổ biến.

Đường cong ROC được sử dụng để đánh giá kết quả của các dự đoán và ứng dụng đầu tiên của nó là trong việc nghiên cứu các hệ thống nhận diện tín hiệu radio khi có sự hiện diện của nhiễu từ những năm 1940, sau sự kiện tấn công Pearl Harbor. Công trình nghiên cứu đầu tiên nhằm mục đích xác định lý do tại sao các 'bộ điều khiển thu nhận' của quân đội Mỹ lại bỏ qua tín hiệu từ máy bay Nhật.

Vào những năm 1960, đường cong ROC bắt đầu được sử dụng trong lĩnh vực tâm lý vật lý (tiếng Anh:

psychophysics) để đánh giá khả năng phát hiện của con người (và thường là của động vật) đối với các tín hiệu yếu. Chúng cũng chứng minh hiệu quả trong việc đánh giá kết quả của máy học, như việc đánh giá các công cụ tìm kiếm trên Internet. Đường cong ROC cũng được sử dụng mạnh mẽ trong dịch tễ học và nghiên cứu y khoa, thường được áp dụng trong điều trị bệnh dựa trên triệu chứng.

Phương pháp dự đoán tốt nhất có thể sẽ cho ra đồ thị là một điểm ở góc trên bên trái của không gian ROC, ví dụ: 100% Độ nhạy (mọi true positives đều được tìm thấy) và 100% Đặc trưng (không có false positives nào cả). Bộ dự đoán ngẫu nhiên sẽ cho kết quả là một đường thẳng tạo một góc 45 độ với trục hoành, tính từ phía dưới bên trái đến phía trên bên phải: điều này là vì, khi ngưỡng tăng, sẽ có cùng số lượng true positives và false positives giảm đi.

Tính chất

Đường cong đi theo biên trái và rồi đi theo biên phía trên của không gian ROC, thể hiện kết quả kiểm tra càng chính xác.
Đường cong tiến tới thành đường chéo 45 độ trong không gian ROC, thể hiện độ chính xác của kiểm tra kém đi.
Hệ số góc của đường thẳng tiếp tuyến tại một điểm cutpoint cho ta tỉ lệ likelihood ratio (LR) của giá trị cutpoint đó của bài kiểm tra.
Diện tích phía dưới đường cong trong không gian ROC là thước đo cho độ chính xác của bài kiểm tra, ví dụ: 1 là tối ưu, 0.5 là kém. Phần diện tích này là thước đo cho khả năng phân biệt tốt hay xấu.

Để tính diện tích này, có 2 phương pháp thường dùng (không dùng tham số - non-parametric và có dùng tham số - parametric), thường được thực hiện thành các chương trình máy tính. Kết quả cho ra là diện tích và sai số chuẩn dùng để so sánh giữa các phép kiểm tra khác nhau, hoặc trong cùng một phép kiểm tra với số lượng cá thể khác nhau.

Ứng dụng

Đôi khi, đường cong ROC được sử dụng để tóm tắt thống kê. Có ba dạng chính thường được áp dụng:

Giao điểm của đường cong ROC với đường thẳng vuông góc 90 độ với đường phân loại (no-discrimination line)
Diện tích dưới đường cong ROC và đường phân loại (no-discrimination line)
Diện tích dưới đường cong ROC, hay gọi là AUC
d ' (phát âm tiếng Anh là 'd-prime'), được tính bằng khoảng cách giữa giá trị trung bình của phân phối hoạt động trong hệ thống dưới điều kiện có nhiễu và phân phối của nó dưới điều kiện tín hiệu và nhiễu, chia cho độ lệch chuẩn của chúng, với giả thiết là cả hai phân phối này là chuẩn với cùng độ lệch chuẩn.

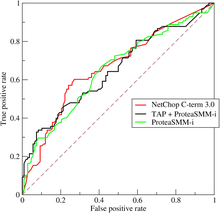
Đường cong ROC của ba hệ thống dự đoán epitope

Tuy nhiên, nếu cố gắng biến đường cong ROC thành một giá trị số duy nhất thì sẽ mất đi thông tin về mô hình của các sự đánh đổi cụ thể trong thuật toán phân loại.

Trong kỹ thuật, diện tích giữa đường cong ROC và đường thẳng tham chiếu thường được sử dụng nhiều nhất, do tính chất toán học hữu ích của nó trong thống kê không tham số. Diện tích này thường được gọi đơn giản là khác biệt (discrimination.) Trong lĩnh vực psychophysics, d ' là chỉ số đánh giá phổ biến nhất.

Hình minh họa bên chỉ ra việc sử dụng đồ thị ROC để biểu thị sự khác biệt giữa các thuật toán dự đoán epitope khác nhau. Để phát hiện ít nhất 60% epitope trong protein của một virus, người dùng có thể sử dụng đồ thị để nhận biết rằng khoảng 1/3 dữ liệu được đánh dấu nhầm là epitope.

Liên kết ngoài

Receiver Operating Characteristic bibliography Lưu trữ 2006-02-16 tại Wayback Machine
Một ví dụ đơn giản về đường cong ROC
Một phần xử lý chi tiết hơn về đường cong ROC và lý thuyết phát hiện tín hiệu Lưu trữ 2010-07-02 tại Wayback Machine

Phần mềm

AccuROC
Các ứng dụng đồ thị ROC
MedCalc Lưu trữ 2005-11-05 tại Wayback Machine
Công cụ tính toán đồ thị ROC trên web Lưu trữ 2006-03-08 tại Wayback Machine
ROCKIT Lưu trữ 2006-05-11 tại Wayback Machine

Theovi.wikipedia.org

Copy link

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]

Các câu hỏi thường gặp

Đường cong ROC là gì và có ý nghĩa gì trong phát hiện tín hiệu?

Đường cong ROC (Receiver Operating Characteristic) là biểu đồ thể hiện mối quan hệ giữa độ nhạy và (1 - đặc trưng) của hệ thống phân loại nhị phân, giúp đánh giá khả năng phát hiện tín hiệu khi có nhiễu.

Tại sao đường cong ROC được sử dụng trong các hệ thống nhận diện tín hiệu?

Đường cong ROC rất quan trọng trong hệ thống nhận diện tín hiệu vì nó giúp phân tích hiệu suất của các dự đoán, cho phép xác định mức độ chính xác trong việc phân loại tín hiệu và nhiễu.

Diện tích dưới đường cong ROC (AUC) có ý nghĩa gì trong đánh giá mô hình?

Diện tích dưới đường cong ROC (AUC) là thước đo cho độ chính xác của mô hình, với giá trị 1 thể hiện mô hình hoàn hảo và 0.5 thể hiện mô hình không có khả năng phân biệt.

Các ứng dụng thực tế của đường cong ROC trong y tế và tâm lý học là gì?

Trong y tế, đường cong ROC được sử dụng để đánh giá khả năng chẩn đoán bệnh dựa trên triệu chứng. Trong tâm lý học, nó giúp phân tích khả năng phát hiện tín hiệu yếu từ đối tượng thử nghiệm.

Làm thế nào để tính diện tích dưới đường cong ROC trong các nghiên cứu?

Có hai phương pháp chính để tính diện tích dưới đường cong ROC: phương pháp không tham số và có tham số. Những phương pháp này thường được thực hiện qua phần mềm máy tính để so sánh giữa các kiểm tra khác nhau.