Đường parabol

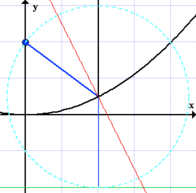
Trong toán học, parabol (tiếng Anh là parabola, từ tiếng Hy Lạp παραβολή) là một đường conic được hình thành từ giao điểm giữa một hình nón và một mặt phẳng song song với đường sinh của hình nón. Một parabol cũng có thể được định nghĩa là tập hợp các điểm trên mặt phẳng cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn).

Trường hợp đặc biệt xảy ra khi mặt phẳng cắt tiếp xúc với mặt nón. Trong tình huống này, giao tuyến trở thành một đường thẳng.

Khái niệm parabol rất quan trọng trong toán học trừu tượng. Tuy nhiên, nó cũng thường xuất hiện trong thực tế, đặc biệt là trong kỹ thuật, vật lý và nhiều lĩnh vực khác.

Các phương trình hình học của parabol

Trong hệ tọa độ Descartes, nếu một parabol có trục đối xứng song song với trục $y$ và đỉnh của nó là $(h,k)$, tiêu cự là $(h,k+p)$, và đường chuẩn là $y=k-<!--\; -\; -->p$, trong đó $p$ là khoảng cách từ đỉnh tới tiêu cự, thì phương trình của parabol sẽ như sau:

$(x-<!--\; -\; -->h{)}^2=4p(y-<!--\; -\; -->k)$

hoặc, với trục song song với trục x

$(y-<!--\; -\; -->k{)}^2=4p(x-<!--\; -\; -->h)=h(x-<!--\; -\; -->h)/4$

Một parabol tổng quát là một đường cong trên mặt phẳng Descartes được xác định bởi một phương trình đơn giản với dạng

$A{x}^2+Bxy+C{y}^2+Dx+Ey+F=0$

trong đó $B^2=4AC$, tất cả các hệ số đều là số thực và $A\ne 0$ hoặc $C\ne 0$, và phương trình có nhiều hơn một nghiệm, xác định tất cả các cặp (x;y) nằm trên parabol, được gọi là phương trình đơn giản nếu nó không thể phân tích thành tích của hai phương trình tuyến tính (không cần phải khác nhau).

Các định nghĩa hình học khác

Một parabol cũng có thể được coi là một đường conic có độ tâm sai bằng 1. Theo định nghĩa này, tất cả các parabol đều đồng dạng với nhau. Một cách để tạo ra một parabol là xem xét giới hạn của một dãy các elip, trong đó một tiêu điểm cố định trong khi tiêu điểm còn lại dời xa. Theo cách hiểu này, parabol có thể xem như là một elip với một tiêu cự vô hạn. Parabol cũng có thể được coi là một ảnh nghịch đảo của một cardioid (đường hình tim).

Một parabol chỉ có một trục đối xứng duy nhất, chạy qua tiêu điểm và vuông góc với đường chuẩn của nó. Giao điểm của trục này với parabol gọi là đỉnh. Nếu một parabol được quay quanh trục của nó trong không gian ba chiều, nó sẽ tạo ra một hình paraboloid.

Parabol xuất hiện trong nhiều tình huống của thế giới vật lý (xem chi tiết dưới đây).

Các phương trình

(với đỉnh (h, k) và khoảng cách p giữa đỉnh và tiêu điểm - lưu ý rằng nếu đỉnh nằm dưới tiêu điểm và trên đường chuẩn thì p sẽ dương, ngược lại thì p sẽ âm; tương tự, đối với trục đối xứng ngang, p dương nếu đỉnh nằm bên trái tiêu điểm và bên phải đường chuẩn).

$(x-<!--\; -\; -->h{)}^2=4p(y-<!--\; -\; -->k)$

$y=a(x-<!--\; -\; -->h{)}^2+k$

$y=a{x}^2+bx+c$

trong đó:$a=\frac{1}{4p};b=\frac{-<!--\; -\; -->h}{2p};c=\frac{h^2}{4p}+k;$

$h=\frac{-<!--\; -\; -->b}{2a};k=\frac{4ac-<!--\; -\; -->b^2}{4a}$.

$x\left(t\right)=2pt+h;y\left(t\right)=p{t}^2+k$

$(y-<!--\; -\; -->k{)}^2=4p(x-<!--\; -\; -->h)$

$x=a(y-<!--\; -\; -->k{)}^2+h$

$x=a{y}^2+by+c$

Trong đó:$a=\frac{1}{4p};b=\frac{-<!--\; -\; -->k}{2p};c=\frac{k^2}{4p}+h;$

$h=\frac{4ac-<!--\; -\; -->b^2}{4a};k=\frac{-<!--\; -\; -->b}{2a}$.

$x\left(t\right)=p{t}^2+h;y\left(t\right)=2pt+k$

Dạng tổng quát của phương trình parabol là:

$(Ax+By{)}^2+Cx+Dy+E=0$

được rút ra từ phương trình tổng quát của các đường conic và đặc điểm của parabol $B^2=4AC$.

Trong hệ tọa độ cực, một parabol có tiêu điểm ở gốc và đường chuẩn nằm trên trục dương x có phương trình là

$r(1+\cos <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->})=l$

trong đó, l là bán tiêu: khoảng cách từ tiêu điểm đến chính parabol, đo dọc theo đường thẳng vuông góc với trục đối xứng. Chú ý rằng khoảng cách này gấp đôi khoảng cách từ tiêu điểm đến đỉnh của parabol và bằng một nửa bán kính qua tiêu.

Bán kính qua tiêu và một đoạn dây cung đi qua tiêu điểm chính và vuông góc với trục đối xứng có độ dài bằng 4a.

Theo biểu thức Gauss-mapped: $({\tan }^2<!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->},2\tan <!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->})$ với pháp tuyến $(\cos <!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->},\sin <!--\; \; -->\mathrm{\varphi <!--\; \varphi \; -->})$.

Xác định tiêu điểm

Xem xét một parabol có đỉnh tại (0,0) và phương trình như sau

$y=a{x}^2,\left(1\right)$

Với điểm tọa độ (0,f) — tiêu điểm — thì bất kỳ điểm P trên parabol luôn có khoảng cách bằng từ điểm đó đến tiêu điểm và từ điểm đó đến đường thẳng vuông góc với trục đối xứng của parabol (đường chuẩn), đường này song song với trục x. Nếu điểm P trùng với đỉnh, thì đường chuẩn sẽ đi qua điểm tọa độ (0,-f). Do đó, với điểm P=(x,y), khoảng cách từ điểm này tới (0,f) và tới (x,-f) là như nhau. Cần tính giá trị f để thỏa mãn điều kiện này.

Giả sử điểm F là tiêu điểm và điểm Q có tọa độ (x,-f). Khoảng cách từ điểm P đến điểm F bằng khoảng cách từ điểm P đến điểm Q.

$\Vert <!--\; \Vert \; -->FP\Vert <!--\; \Vert \; -->=\sqrt{x^2+(y-<!--\; -\; -->f{)}^2},$

Bình phương cả hai vế của phương trình,

$x^2+a^2{x}^4+f^2-<!--\; -\; -->2a{x}^{2}f=a^2{x}^4+f^2+2a{x}^{2}f$

Rút gọn hai vế phương trình, ta có:

$x^2-<!--\; -\; -->2a{x}^{2}f=2a{x}^{2}f,$

$x^2=4a{x}^{2}f.$

Chia cả hai vế cho x² (với x khác không),

$1=4af$

$f=\frac{1}{4a}$

Đặt p=f và công thức của parabol trở thành

$x^2=4py$

Công thức tổng quát cho mọi parabol, ở dạng chuẩn

$y=a{x}^2+bx+c$,

tọa độ của điểm cực trị là

có thể được diễn tả lại như sau

và đường chuẩn được tính theo công thức sau:

có thể được diễn đạt như sau

Tính phản xạ tại điểm tiếp xúc

Về mặt toán học, mọi tia phát xuất từ một điểm cụ thể và song song với trục đối xứng của parabol đều phản chiếu đối xứng với tia phát xuất từ điểm đó đi qua đỉnh và vuông góc với tiếp tuyến tại điểm đó.

Xét về góc độ vật lý, bất kỳ tia sáng nào đi dọc theo trục đối xứng vào phần lõm của một gương parabol đều sẽ phản xạ qua tiêu điểm.

Khi thay đổi giá trị của b

Xác định tung độ của đỉnh parabol

Chúng ta đã biết hoành độ của đỉnh parabol là , và ta có thể thay vào phương trình $y=a{x}^2+bx+c$

$y=a{\left(-<!--\; -\; -->\frac{b}{2a}\right)}^2+b\left(-<!--\; -\; -->\frac{b}{2a}\right)+c$ Được đơn giản hóa

Do đó, tọa độ đỉnh của đồ thị là…

$\left(-<!--\; -\; -->\frac{b}{2a},-<!--\; -\; -->\frac{D}{4a}\right)$

Đường parabol trong thực tế vật lý

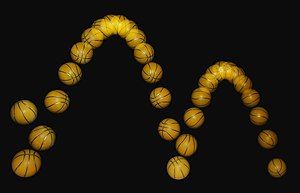
Trong tự nhiên, hình dạng gần giống parabol và các vật thể có hình dạng paraboloid xuất hiện phổ biến. Ví dụ nổi tiếng nhất về hình parabol trong vật lý là quỹ đạo của vật ném xiên dưới tác động của trọng lực khi không có lực cản không khí (như một quả bóng chày bay trong không khí, bỏ qua lực cản của không khí). Đường bay hình parabol được phát hiện bởi Galileo vào đầu thế kỷ XVII qua các thí nghiệm về chuyển động của quả bóng trên mặt phẳng nghiêng. Ông đã chứng minh điều này bằng phương pháp toán học trong cuốn 'Đối thoại về hai ngành khoa học mới'. Đối với vật thể lớn, như một vận động viên nhảy cầu, mặc dù vật thể có thể quay và di chuyển phức tạp, trọng tâm của nó vẫn theo hình parabol. Dù có lực cản không khí, quỹ đạo chuyển động của vật vẫn gần giống hình parabol. Ở tốc độ cao hơn, như với viên đạn, quỹ đạo sẽ bị biến dạng và không còn giống hình parabol.

Một số ví dụ khác về hình parabol trong tự nhiên bao gồm quỹ đạo của các thiên thể như tiểu hành tinh dưới ảnh hưởng của trọng lực mặt trời. Quỹ đạo hình parabol là một trường hợp hiếm gặp, thường thì quỹ đạo là hình elip hoặc hyperbol. Quỹ đạo parabol là dạng chuyển tiếp giữa hai loại quỹ đạo này, nơi vật thể di chuyển với tốc độ tới hạn để thoát khỏi vật thể mà nó quay quanh, với tốc độ này nhanh hơn hình elip nhưng chậm hơn hình hyperbol.

Các cầu treo có cáp tạo thành hình dạng gần giống parabol. Mặc dù các cáp đỡ ban đầu có hình vòng cung, dưới tác động của trọng lực và các lực khác, chúng sẽ dần dần bị biến dạng thành hình parabol.

Hình paraboloid xuất hiện trong một số trường hợp đặc biệt. Ví dụ điển hình nhất là gương paraboloid, là các tấm gương hoặc mảnh kim loại có khả năng phản chiếu và hội tụ ánh sáng hoặc sóng điện từ tại một điểm. Archimedes vào thế kỉ III trước Công Nguyên đã phát hiện tính chất này và ghi lại truyền thuyết về việc sử dụng gương paraboloid để bảo vệ Syracuse khỏi quân La Mã bằng cách hội tụ ánh sáng mặt trời để đốt cháy tàu chiến của họ. Tính chất này cũng được áp dụng để chế tạo kính viễn vọng vào thế kỷ XVII. Ngày nay, gương paraboloid được sử dụng rộng rãi trong các ăng ten vi sóng và chảo vệ tinh.

Các hình paraboloid xoay có thể được quan sát trên bề mặt các chất lỏng trong bình chứa xoay quanh một trục trung tâm. Trong tình huống này, lực li tâm khiến chất lỏng dâng lên phía thành bình, tạo thành mặt parabol. Nguyên lý này được ứng dụng trong gương chất lỏng.

Các máy bay tạo môi trường không trọng lực cho thí nghiệm, chẳng hạn như các 'Vomit Comet' của NASA, bay theo quỹ đạo parabol đứng trong thời gian ngắn để tạo ra môi trường phi trọng lực.

• Đường cô-nic
• Elip
• Hyperbol
• Gương Paraboloid
• Paraboloid

Chú thích

Liên kết ngoài

• Khám Phá Parabol của Apollonius tại
• Weisstein, Eric W., 'Parabola' từ MathWorld.
• Chế độ kéo thả parabola tương tác, xem trục đối xứng, đường chính, các dạng chuẩn và đỉnh
• Tam giác Archimedes và Phép Đo Parabol tại Cut-The-Knot
• Hai tiếp tuyến của Parabol tại Cut-The-Knot
• Parabol Là Đường Bao Của Các Đường Thẳng tại Cut-The-Knot
• Gương Parabol tại Cut-The-Knot
• Ba tiếp tuyến của Parabol tại Cut-The-Knot
• Module cho Parabol Tiếp Tuyến
• Thuộc Tính Tiêu Điểm Của Parabol tại Cut-The-Knot
• Parabol Là Đường Bao II tại Cut-The-Knot
• Xây Dựng Parabol - Một bản vẽ tương tác cho thấy cách vẽ parabol. (Cần Java.)
• Xây Dựng Bezier Quadratic Lưu trữ 2007-11-06 tại Wayback Machine - Một bản vẽ tương tác cho thấy cách vẽ đường Bezier quadratic (một đoạn parabol). (Cần Java.)
• Thêm Xây Dựng Parabol Tương Tác (Yêu cầu Java)