Đường thẳng Simson

Trong hình học, định lý về đường thẳng Simson được diễn đạt như sau:

Cho tam giác $ABC$ và một điểm $P$ nằm trên đường tròn ngoại tiếp của tam giác. Các hình chiếu của điểm $P$ lên các cạnh của tam giác nằm trên một đường thẳng. Đường thẳng đi qua các hình chiếu này được gọi là Đường thẳng Simson' của điểm $P$ đối với tam giác $ABC$. Đường thẳng này được đặt theo tên của nhà toán học Robert Simson, mặc dù khái niệm này được công bố lần đầu bởi William Wallace.

Mệnh đề đảo của định lý này cũng đúng: Nếu các hình chiếu của một điểm $P$ trên các cạnh của một tam giác nằm trên một đường thẳng, thì điểm $P$ phải nằm trên đường tròn ngoại tiếp của tam giác đó.

Đường thẳng Simson của một điểm tương đương với tam giác bàn đạp của điểm đó, ngoại trừ trường hợp tam giác trở thành đường thẳng.

Tính chất

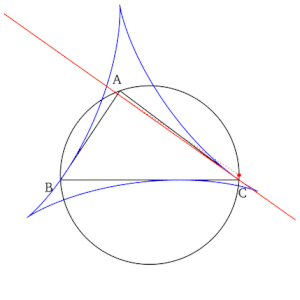
Xét tam giác $ABC$ nội tiếp đường tròn $\left(O\right)$.

Xem xét các đường thẳng Simson của các điểm trên đường tròn $\left(O\right)$.

• Đường thẳng Simson của đỉnh $A$ của tam giác là đường cao từ đỉnh đó, trong khi đường thẳng Simson của điểm $A^{\prime }$, đối xứng với đỉnh $A$
  {\displaystyle A} qua tâm $O$, chính là cạnh $BC$ của tam giác.

Phát triển

Phát triển 1

Cho điểm P {\displaystyle P} trên đường tròn ngoại tiếp của tam giác A B C {\displaystyle ABC} , và một đường thẳng d {\displaystyle d} đi qua tâm của đường tròn đó. Ba đường thẳng A P , B P , C P {\displaystyle AP,BP,CP} cắt đường thẳng d {\displaystyle d} tại ba điểm phân biệt A p , B p , C p {\displaystyle A_{p},B_{p},C_{p}} . Khi đó, các hình chiếu của ba điểm A p , B p , C p {\displaystyle A_{p},B_{p},C_{p}} tương ứng trên ba cạnh B C , C A , A B {\displaystyle BC,CA,AB} sẽ thẳng hàng. Đã có bốn chứng minh cho sự phát triển này.

Mở rộng 2

Cho một điểm $P$ trong mặt phẳng và một đường conic, ba đường thẳng khác nhau đi qua $P$. Đường thẳng đầu tiên cắt conic tại các điểm $A$, $A^{\prime }$. Định nghĩa các điểm $B$, $B^{\prime }$ và $C$, $C^{\prime }$ tương tự. Đặt $S$ là điểm trong mặt phẳng, và gọi $A_0$, $B_0$, $C_0$ là ba điểm giao của ba đường thẳng $S{A}^{\prime }$, $S{B}^{\prime }$, $S{C}^{\prime }$ với ba cạnh tam giác $BC$, $CA$, $AB$ của tam giác $ABC$ thì bốn điểm $P$, $S$, $A$, $B$ và $C$ cùng nằm trên một đường thẳng.

Mở rộng này của Lazare Carnot, một nhà toán học nổi tiếng người Pháp.

Giả sử D là một điểm trên đường tròn ngoại tiếp tam giác ABC, và các điểm A0, B0, C0 nằm lần lượt trên các cạnh BC, CA, AB. Khi đó, nếu góc tạo bởi các đường thẳng DA0, DB0, DC0 với ba cạnh BC, CA, AB là bằng nhau, thì ba điểm A0, B0, C0 sẽ nằm trên một đường thẳng.

• Tam giác bàn đạp
• Robert Simson
• Định lý Sondat
• Định lý Đào (Conic)
• Định lý Carnot
• Định lý Đào (mở rộng đường thẳng Simson)

Ghi chú

Các liên kết bên ngoài

• Đường Simson
• F. M. Jackson và Weisstein, Eric W., 'Đường Simson', MathWorld.
• Mở rộng của định lý Neuberg và đường Simson-Wallace Lưu trữ 2011-07-18 tại Wayback Machine ở Dynamic Geometry Sketches Lưu trữ 2009-03-21 tại Wayback Machine