Đường tròn Euler

Trong hình học, đường tròn chín điểm (tiếng Anh: nine-point circle) là một đường tròn được xây dựng từ bất kỳ tam giác nào. Đường tròn này đi qua chín điểm đặc biệt của tam giác, bao gồm:

• Trung điểm của mỗi cạnh của tam giác
• Chân của các đường cao từ mỗi đỉnh của tam giác
• Trung điểm của đoạn thẳng nối đỉnh của tam giác với trực tâm (nơi ba đường cao giao nhau)

Đường tròn chín điểm còn được gọi với các tên khác như đường tròn của Feuerbach (theo tên nhà toán học Karl Wilhelm Feuerbach), đường tròn của Euler (theo tên nhà toán học Leonhard Euler), đường tròn của Terquem (theo tên nhà toán học Olry Terquem), đường tròn sáu điểm, đường tròn mười hai điểm, đường tròn n-điểm, hay đường tròn trung bình. Tâm của đường tròn này được gọi là tâm chín điểm của tam giác.

Chín điểm quan trọng

Hình bên phải minh họa chín điểm quan trọng trên đường tròn Euler. Các điểm D, E và F là trung điểm của ba cạnh của tam giác, trong khi các điểm G, H và I là chân của ba đường cao. Các điểm J, K và L là trung điểm của các đoạn nối giữa ba đỉnh của tam giác và trực tâm của nó.

Đối với tam giác nhọn, sáu trong số chín điểm (trung điểm các cạnh và chân các đường cao) nằm ngay trên tam giác đó. Đối với tam giác tù, hai chân của đường cao có thể nằm ngoài tam giác, nhưng chúng vẫn nằm trên đường tròn Euler.

Khám phá

Dù được đặt tên theo Karl Wilhelm Feuerbach, người đã không chứng minh hoàn toàn đường tròn chín điểm mà chỉ chứng minh sáu điểm (trung điểm các cạnh và chân đường cao) trên một đường tròn, việc chứng minh đầy đủ về đường tròn chín điểm được thực hiện sau đó bởi Olry Terquem. Ông là người đầu tiên nhận ra rằng các trung điểm của đoạn nối đỉnh tam giác và trực tâm cũng nằm trên đường tròn này, và vì vậy ông đã đặt tên cho nó là đường tròn chín điểm như ngày nay.

Đường tròn tiếp xúc

Năm 1822, Karl Feuerbach đã chứng minh rằng đường tròn chín điểm của một tam giác giao với ba đường tròn bàng tiếp và đường tròn nội tiếp của tam giác đó. Kết quả này được gọi là định lý Feuerbach, theo đó ông phát biểu rằng:

Đường tròn đi qua các chân của đường cao trong tam giác, tiếp xúc với bốn đường tròn lần lượt tiếp xúc với các cạnh của tam giác.

Điểm mà đường tròn chín điểm giao với đường tròn nội tiếp được gọi là điểm Feuerbach.

Đặc điểm

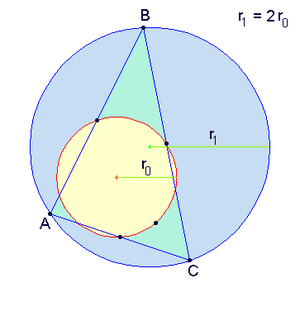
• Đường tròn Euler của một tam giác có bán kính bằng một nửa bán kính đường tròn ngoại tiếp (R/2) và tâm của nó là trung điểm của đoạn nối giữa trực tâm và tâm đường tròn ngoại tiếp.
• Khi có một hệ trực giao của 4 điểm, các tam giác có đỉnh là 3 trong số 4 điểm đó đều chia sẻ cùng một đường tròn Euler.
• Các tâm của đường tròn nội tiếp và các đường tròn bàng tiếp tạo thành một hệ trực giao, trong đó đường tròn Euler chính là đường tròn ngoại tiếp của tam giác gốc.
• Với bất kỳ bốn điểm phân biệt nào A, B, C, D, các đường tròn Euler của các tam giác ABC, BCD, CDA, DAB đều gặp nhau tại một điểm chung.

Định lý liên quan

• Định lý Feuerbach về các đường tròn nội tiếp và bàng tiếp: Đường tròn Euler của một tam giác tiếp xúc với cả đường tròn nội tiếp và ba đường tròn bàng tiếp của tam giác đó.
• Định lý Feuerbach đối với đường hyperbol chữ nhật trong tam giác: Tất cả các đường hyperbol chữ nhật đều có tâm nằm trên đường tròn Euler.

• Định lý Bliss: Ba đường thẳng song song đi qua ba trung điểm của ba cạnh trong tam giác khi đối xứng của ba cạnh qua các đường thẳng này sẽ đồng quy tại đường tròn chín điểm của tam giác đó.
• Định lý Thebault: Trong tam giác ABC với các đường cao AA', BB', CC', các đường thẳng Euler của các tam giác AB'C', A'BC', và A'B'C sẽ đồng quy tại điểm trên đường tròn Euler của tam giác ABC sao cho một trong các khoảng cách PA', PB', PC' bằng tổng của hai khoảng cách còn lại.

Hệ thức

Thêm

• Đường hyperbol
• Định lý Fontene

Liên kết bên ngoài

(tiếng Anh)

• Bách khoa toàn thư về Trung tâm Tam giác của Clark Kimberling. Trung tâm chín điểm được chỉ mục là X(5), điểm Feuerbach là X(11), trung tâm của hyperbol Kiepert là X(115), và trung tâm của hyperbol Jerabek là X(125).
• Trung tâm Chín Điểm của Antonio Gutierrez từ Geometry Step by Step từ vùng đất của người Inca.
• Lịch sử về đường tròn chín điểm dựa trên bài viết của J.S. MacCay từ năm 1892: Lịch sử của Đường tròn Chín điểm Lưu trữ 2013-09-20 tại Wayback Machine
• Đường tròn chín điểm trên Java tại Cut-The-Knot
• Định lý Feuerbach: một chứng minh tại Cut-The-Knot
• Các đường thẳng và đường tròn đặc biệt trong tam giác Lưu trữ 2006-04-05 tại Wayback Machine (cần Java)
• Ứng dụng Java tương tác cho thấy nhiều trung tâm tam giác nằm trên Đường tròn Chín điểm Lưu trữ 2016-04-04 tại Wayback Machine.