Đường tròn nội tiếp và đường tròn ngoại tiếp

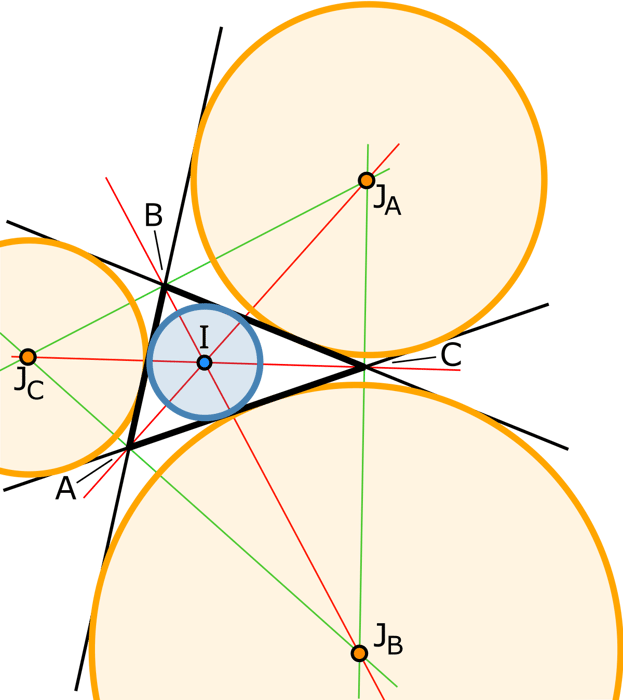
Trong hình học, đường tròn nội tiếp của tam giác là đường tròn lớn nhất nằm bên trong tam giác, tiếp xúc với ba cạnh của tam giác. Tâm của đường tròn nội tiếp là điểm giao của ba đường phân giác trong tam giác.

Một đường tròn ngoại tiếp của tam giác là một đường tròn nằm ngoài tam giác, tiếp xúc với một cạnh của tam giác và với phần mở rộng của hai cạnh còn lại. Mọi tam giác đều có ba đường tròn ngoại tiếp, mỗi đường tròn tiếp xúc với một cạnh. Tâm của một đường tròn ngoại tiếp là điểm giao của đường phân giác trong của một góc với các đường phân giác ngoài của hai góc còn lại.

Công thức bán kính

Xét tam giác ABC có các cạnh lần lượt là a, b, c và diện tích S; r, r_a, r_b, r_c lần lượt là bán kính đường tròn nội tiếp và các đường tròn ngoại tiếp với các cạnh a, b, c. Đặt p = (a + b + c) / 2. Khi đó có các công thức cơ bản sau: r = 2S / (a + b + c) = S / p = (p - a)tan(A/2) = (p - b)tan(B/2) = (p - c)tan(C/2) = √((p-a)(p-b)(p-c)/p).

Bán kính đường tròn nội tiếp với cạnh a của tam giác ABC được tính bằng công thức ra là ra = 2S / (b + c - a) = S / (p - a) = p.tan(A/2).

Bán kính đường tròn ngoại tiếp với cạnh b của tam giác ABC được tính bằng công thức ra là rb = 2S / (c + a - b) = S / (p - b) = p.tan(B/2).

$\begin{array}{c}{r}_c=\frac{2S}{a+b-<!--\; -\; -->c}=\frac{S}{p-<!--\; -\; -->c}=p.\tan <!--\; \; -->\frac{C}{2}\end{array}$

Một số tính chất của các tâm

• Tâm của bốn đường tròn này cách đều các cạnh của tam giác
• Đường tròn nội tiếp và các đường tròn bàng tiếp đều tiếp xúc với đường tròn chín điểm. Tiếp điểm của đường tròn nội tiếp với đường tròn chín điểm gọi là điểm Feuerbach.
• Các tâm của đường tròn nội tiếp và các đường tròn bàng tiếp lập thành một hệ thống trực giao có đường tròn chín điểm chính là đường tròn ngoại tiếp của tam giác.
• Cho tam giác ABC, đường tròn nội tiếp tiếp xúc với ba cạnh tam giác tại ba điểm A', B', C' khi đó ba đường thẳng AA', BB'. CC' đồng quy. Điểm này gọi là điểm Gergonne của tam giác
• Cho tam giác ABC, đường tròn bàng tiếp ứng với cạnh BC, CA, AB lần lượt tiếp xúc với các cạnh này tại A', B', C' khi đó ba đường thẳng AA', BB'. CC' đồng quy. Điểm này gọi là điểm Nagel của tam giác ABC.

Biểu thức tọa độ

Trên mặt phẳng tọa độ Đề-các, nếu một tam giác có 3 đỉnh có tọa độ là $({\mathrm{x\; <div\; class="min-w-[250px]\; max-w-[94vw]\; md:max-w-[770px]">\; <ins\; class="adsbygoogle"\; style="display:block;\; text-align:center;"\; data-ad-layout="in-article"\; data-ad-format="fluid"\; data-ad-client="ca-pub-9247024304160346"\; data-ad-slot="4115752014"></ins>\; </div>}}_a,y_a)$, $(x_b,y_b)$, $(x_c,y_c)$ ứng với độ dài các cạnh đối diện là $a$, $b$, $c$ thì tâm đường tròn nội tiếp tam giác đó có tọa độ là:

$(\frac{a{x}_a+b{x}_b+c{x}_c}{P},\frac{a{y}_a+b{y}_b+c{y}_c}{P})=\frac{a}{P}(x_a,y_a)+\frac{b}{P}(x_b,y_b)+\frac{c}{P}(x_c,y_c)$.

ở đó $P=a+b+c$