Đường trung tuyến là gì? Tính chất, công thức và bài tập tính đường trung tuyến

Đường trung tuyến là một khái niệm phổ biến trong hình học không gian và thường được áp dụng trong tam giác. Với kiến thức về định nghĩa và công thức tính toán, chúng ta có thể áp dụng chúng để giải quyết các bài toán hình học liên quan đến tam giác một cách dễ dàng. Hãy cùng khám phá về đường trung tuyến là gì và một số bài tập để nắm vững chủ đề này.

Đường trung tuyến là gì?

Đường trung tuyến là một đường thẳng đi qua trung điểm của một đoạn thẳng. Trong tam giác, nó là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến và chúng giao nhau tại trọng tâm của tam giác. Trọng tâm có những tính chất đặc biệt như cách mỗi đỉnh một khoảng bằng hai phần ba độ dài của đường trung tuyến tương ứng.

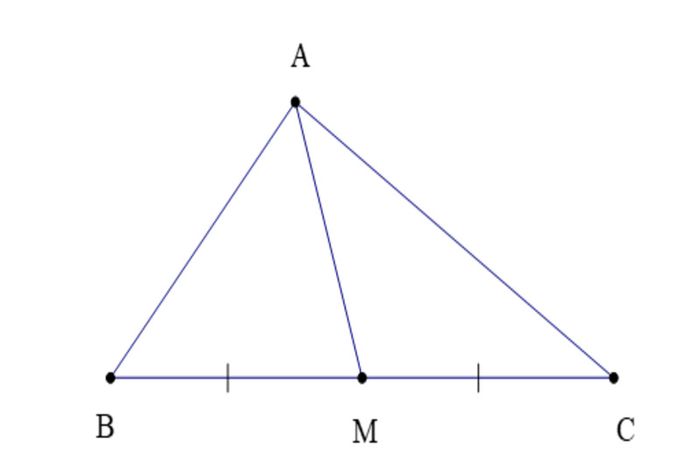
Đường trung tuyến cũng có một đặc điểm quan trọng khác là nó chia diện tích của tam giác thành hai phần bằng nhau. Ba đường trung tuyến cũng chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau. Điều này có thể chứng minh bằng định lý Apollonius hoặc các công thức về diện tích tam giác.

Đường trung tuyến là gì cũng có một số đặc trưng đặc biệt trong các loại tam giác như tam giác vuông, tam giác cân hoặc tam giác đều. Ví dụ, trong tam giác vuông, đường trung tuyến của cạnh huyền bằng một nửa cạnh huyền. Trong tam giác cân, đường trung tuyến của cạnh đáy vuông góc với cạnh đáy và chia tam giác thành hai tam giác bằng nhau. Trong tam giác đều, mỗi đường trung tuyến cũng là đường cao, đường phân giác và đường trung trực của tam giác.

Tính chất của đường trung tuyến là gì?

Tính chất của đường trung tuyến là một trong những khía cạnh quan trọng trong hình học tam giác. Khám phá tính chất của đường trung tuyến giúp chúng ta hiểu sâu hơn về cấu trúc và mối quan hệ trong tam giác. Đường trung tuyến có những tính chất đặc biệt trong từng loại tam giác khác nhau. Dưới đây là một số thông tin cụ thể về tính chất của đường thẳng này:

Trong tam giác cân, đường trung tuyến của cạnh đáy sẽ vuông góc với cạnh đáy và chia tam giác thành hai tam giác bằng nhau. Trong tam giác đều, ba đường trung tuyến đều vuông góc với cạnh đối diện và chia tam giác thành sáu tam giác đều nhỏ.

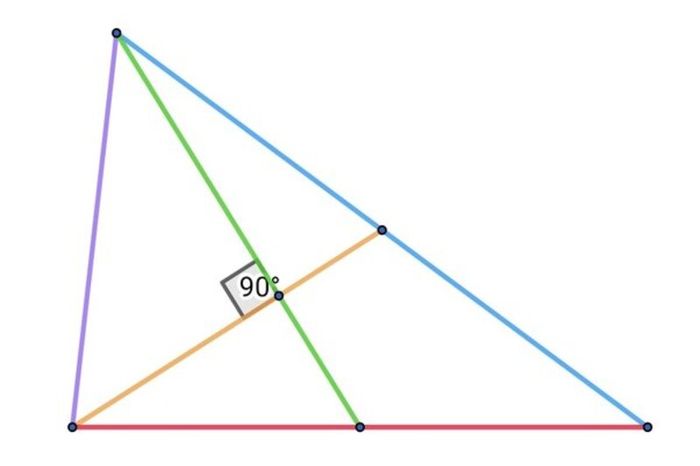
Trong tam giác vuông, đường trung tuyến của cạnh huyền sẽ bằng một nửa độ dài cạnh huyền và chia tam giác vuông thành hai tam giác đồng dạng với tam giác ban đầu. Đường trung tuyến của một cạnh góc vuông sẽ bằng trung bình cộng của độ dài cạnh huyền và cạnh góc vuông đối diện.

Đối với tam giác đồng dạng, tỉ số độ dài của đường trung tuyến của cạnh đối diện sẽ bằng tỉ số độ dài các cạnh tương ứng của hai tam giác. Nghĩa là, nếu tam giác ABC đồng dạng với tam giác A’B’C’ thì AD/BC = A’D’/B’C’.

Những định lí của đường trung tuyến trong hình học

Sau khi nghiên cứu sâu về đường trung tuyến trong tam giác, ta nhận thấy đoạn thẳng này đóng vai trò quan trọng và liên quan đến nhiều định lí hình học. Dưới đây là ba định lí cơ bản về đường trung tuyến trong tam giác.

Hai đường trung tuyến trong tam giác chia nhau một nửa về độ dài.

Định lí này khẳng định rằng hai đường trung tuyến trong tam giác chia nhau thành hai phần bằng nhau về độ dài. Điều này có nghĩa là đường trung tuyến từ một đỉnh của tam giác đến trung điểm của cạnh đối diện có độ dài bằng một nửa đường trung tuyến từ đỉnh còn lại đến trung điểm của cạnh đối diện. Định lí này làm rõ mối quan hệ giữa các đường trung tuyến và các cạnh của tam giác.

Để hiểu sâu hơn về định lí này, hãy xem xét một tam giác bất kỳ. Giả sử ta có tam giác ABC. Đường trung tuyến từ đỉnh A đến trung điểm của cạnh BC sẽ có độ dài bằng một nửa đường trung tuyến từ đỉnh B đến trung điểm của cạnh AC. Tương tự, đường trung tuyến từ đỉnh A đến trung điểm của cạnh AC sẽ có độ dài bằng một nửa đường trung tuyến từ đỉnh C đến trung điểm của cạnh AB. Điều này cho thấy rằng hai đường trung tuyến này chia nhau một nửa về độ dài.

Đoạn thẳng trung tuyến và cạnh tương ứng của tam giác là song song với nhau.

Định lí này xác định mối quan hệ giữa đường trung tuyến và các cạnh của tam giác. Theo đó, đoạn thẳng trung tuyến và cạnh tương ứng của tam giác là hai đường thẳng song song với nhau. Vì vậy, đường trung tuyến từ một đỉnh của tam giác đến trung điểm của cạnh đối diện là song song với cạnh tương ứng. Định lí này làm nổi bật tính chất quan trọng của đường trung tuyến và mối quan hệ của nó với các cạnh của tam giác.

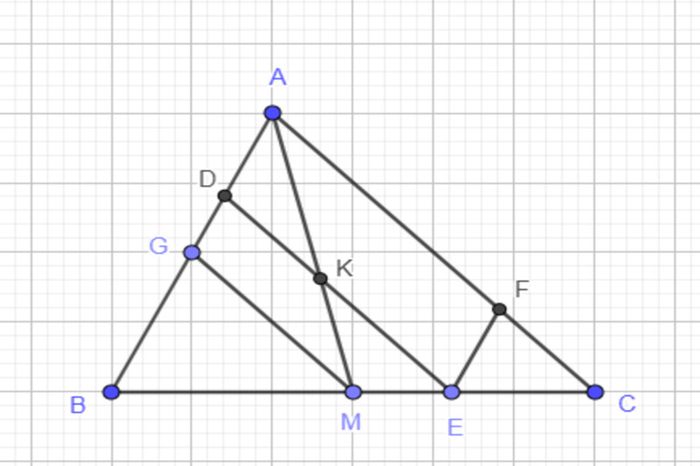
Để hiểu rõ hơn, xét tam giác ABC và đường trung tuyến AH từ đỉnh A đến trung điểm M của cạnh BC. Đường trung tuyến AH và cạnh tương ứng BC tạo thành một đường thẳng duy nhất. Định lí này khẳng định rằng đường này là một đoạn thẳng song song.

Ba đường trung tuyến của tam giác giao nhau tại một điểm duy nhất.

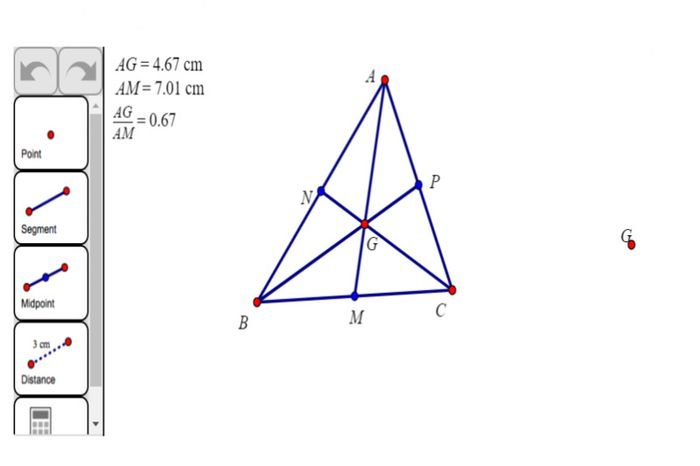
Ba đường trung tuyến của tam giác giao nhau tại một điểm duy nhất, đó chính là trọng tâm của tam giác. Trọng tâm được xác định là trung điểm của các đoạn thẳng nối các đỉnh của tam giác với trung điểm của các cạnh đối diện. Đây là một điểm đặc biệt trong tam giác với những tính chất đáng chú ý.

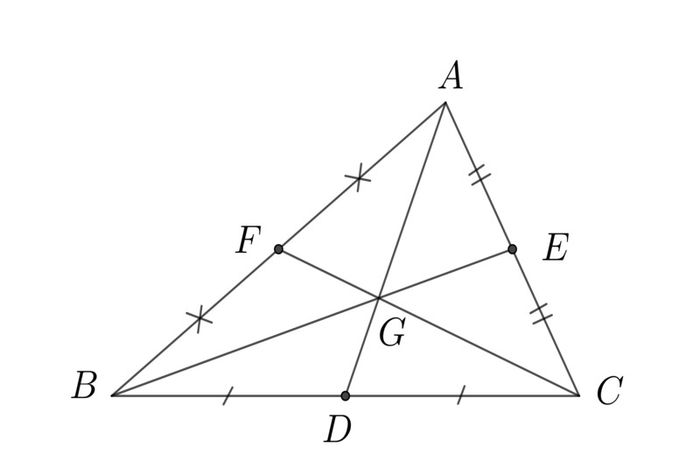
Trọng tâm có một tính chất độc đáo là tổng các vectơ từ trọng tâm đến các đỉnh của tam giác bằng vectơ không. Điều này có nghĩa là nếu ta vẽ các vectơ từ trọng tâm đến các đỉnh và cộng chúng lại, kết quả sẽ là vectơ không. Điều này thể hiện sự cân bằng của tam giác và cho thấy trọng tâm nằm ở trung tâm hình học của tam giác.

Ngoài ra, trọng tâm cũng đặc biệt vì nó chia ba đường trung tuyến thành tỷ lệ 1:2. Điều này có nghĩa là đường trung tuyến từ trọng tâm đến một đỉnh bất kỳ có độ dài gấp đôi so với đường trung tuyến từ trọng tâm đến trung điểm của cạnh đối diện. Tỷ lệ này thể hiện mối quan hệ đặc biệt giữa trọng tâm và các đường trung tuyến, tạo ra sự phân bổ đều và cân bằng trong tam giác.

Công thức tính toán đường trung tuyến là gì?

Để tính toán đường trung tuyến trong tam giác, ta cần biết các thông tin cơ bản về tam giác như độ dài các cạnh và tọa độ các đỉnh. Công thức tính toán đường trung tuyến phụ thuộc vào những thông tin này và có thể áp dụng một cách dễ dàng.

Công thức tính toán tọa độ điểm chính giữa cạnh BC là gì?

Giả sử ta có tam giác ABC với tọa độ các đỉnh lần lượt là A(x1, y1), B(x2, y2), C(x3, y3). Để tính toán tọa độ của điểm D là trung điểm của cạnh BC, ta sử dụng công thức sau:

Tọa độ x của D là trung bình cộng của tọa độ x của B và C, tức là: xD = (x2 + x3) / 2.

Tọa độ y của D là trung bình cộng của tọa độ y của B và C, tức là: yD = (y2 + y3) / 2.

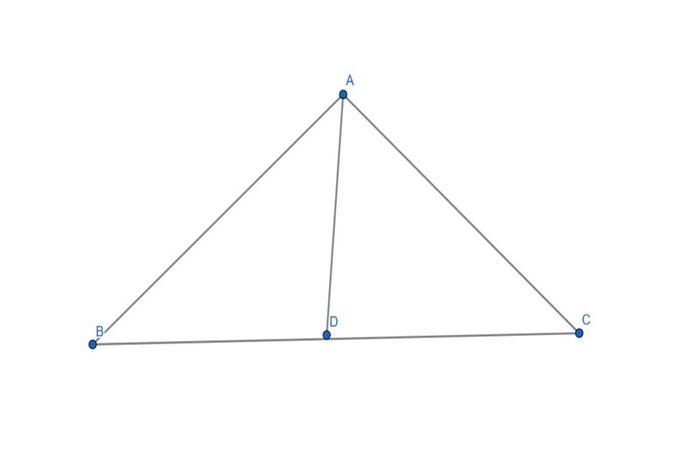
Với x là hoành độ của điểm chính giữa cạnh BC và y là tung độ của điểm chính giữa cạnh BC, ta có tọa độ của D là D((x2 + x3) / 2, (y2 + y3) / 2).

Công thức tính toán tọa độ điểm chính giữa các cạnh còn lại là gì?

Tương tự như trên, dựa vào định nghĩa đường trung tuyến và một số thông tin khác, ta có thể tính toán tọa độ của các điểm E và F là trung điểm của các cạnh AC và AB bằng cách sử dụng công thức sau:

Tọa độ x của E bằng trung bình cộng của tọa độ x của A và C, tức là: xE = (x1 + x3) / 2.

Tọa độ y của E bằng trung bình cộng của tọa độ y của A và C, tức là: yE = (y1 + y3) / 2.

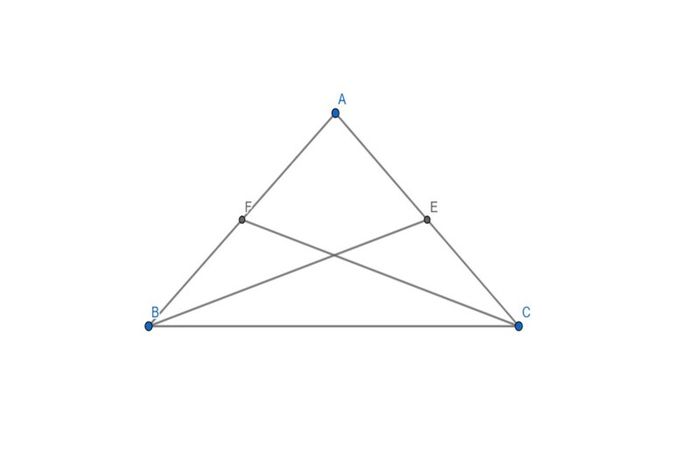
Tọa độ x của F bằng trung bình cộng của tọa độ x của A và B, tức là: xF = (x1 + x2) / 2.

Tọa độ y của F bằng trung bình cộng của tọa độ y của A và B, tức là: yF = (y1 + y2) / 2.

Vậy tọa độ của E là E((x1 + x3) / 2, (y1 + y3) / 2), và tọa độ của F là F((x1 + x2) / 2, (y1 + y2) / 2).

Bài tập áp dụng về đường trung tuyến

Để nắm vững kiến thức về đường trung tuyến và áp dụng chúng vào thực tế, chúng ta cần thực hành qua các bài tập. Với những kiến thức về đường trung tuyến là gì và công thức tính toán của nó, sau đây chúng ta sẽ áp dụng và giải quyết hai bài tập liên quan đến đường trung tuyến.

Bài tập số 1: Tính tọa độ điểm chính giữa cạnh BC và cạnh AC

Cho tam giác ABC có tọa độ các đỉnh là A(1;2), B(3;4) và C(5;6). Tính tọa độ điểm chính giữa cạnh BC và cạnh AC.

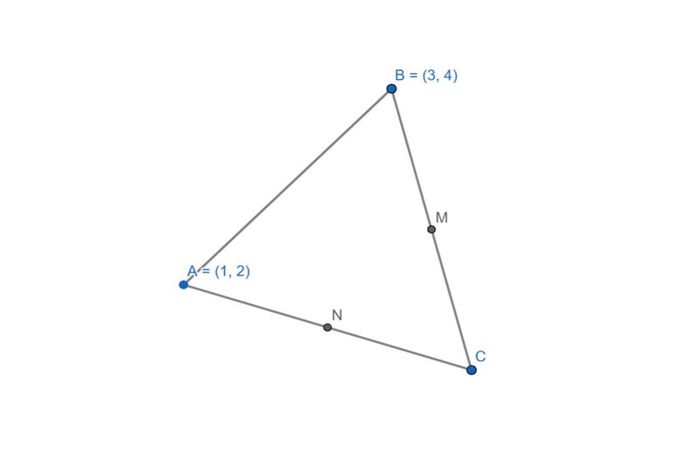
Lời giải:

Để tính tọa độ điểm chính giữa cạnh BC, ta lấy trung bình cộng của tọa độ x và y của hai đỉnh B và C. Ta được: M((3+5)/2; (4+6)/2) = M(4;5).

Để tính tọa độ điểm chính giữa cạnh AC, ta lấy trung bình cộng của tọa độ x và y của hai đỉnh A và C. Ta được: N((1+5)/2; (2+6)/2) = N(3;4)

Vậy tọa độ điểm chính giữa cạnh BC là M(4;5) và tọa độ điểm chính giữa cạnh AC là N(3;4).

Bài tập số 2: Tính tọa độ đỉnh B và đỉnh C dựa trên đường trung tuyến AM

Cho tam giác ABC có tọa độ đỉnh A là A(2;3) và tọa độ trung điểm của cạnh BC là M(4;5). Biết rằng đường trung tuyến AM có phương trình là y = 2x – 1. Tính tọa độ đỉnh B và đỉnh C.

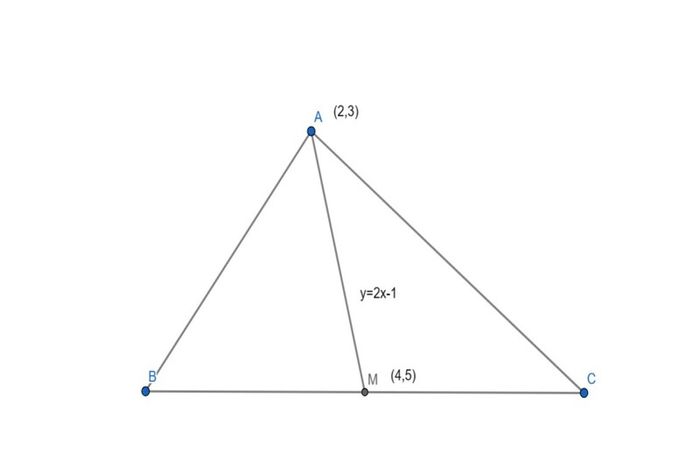
Lời giải:

Để tính tọa độ đỉnh B và đỉnh C, ta cần tìm phương trình của cạnh BC. Ta có những thông tin sau:

• Cạnh BC vuông góc với đường trung tuyến AM, nên hệ số góc của cạnh BC là -1/2 (lấy nghịch đảo đối của hệ số góc của AM).
• Cạnh BC đi qua điểm M(4;5), nên phương trình của cạnh BC có dạng y = -1/2x + b.
• Thay tọa độ điểm M vào phương trình, ta được b = 7. Vậy phương trình của cạnh BC là y = -1/2x + 7.

Bây giờ, ta có thể giải hệ phương trình của cạnh BC và đường trung tuyến AM để tìm tọa độ các đỉnh B và C. Ta có y = -1/2x + 7 y = 2x – 1 và ta được x = 2 và y = 3. Do đó, tọa độ của đỉnh B hoặc đỉnh C là (2;3).

Để tìm tọa độ của đỉnh còn lại, ta dùng tính chất của điểm trung điểm. Ta có: M là trung điểm của BC, nên tọa độ x và y của M bằng trung bình cộng của tọa độ x và y của B và C. Từ đó suy ra 4 = (2 + x)/2 5 = (3 + y)/2

Giải hệ, ta được x = 6 và y = 7 là tọa độ của đỉnh còn lại. Vậy tọa độ đỉnh B là (2;3) và tọa độ đỉnh C là (6;7) hoặc ngược lại.

Kết luận

Qua bài viết này, chúng ta đã nắm được đường trung tuyến là gì và một số thông tin chi tiết khác về đoạn thẳng này. Để nắm vững kiến thức về đường trung tuyến, chúng ta cần ôn tập và luyện tập thường xuyên các bài tập về đường thẳng này, đặc biệt là các dạng bài tập thường gặp. Hy vọng bài viết này sẽ giúp ích cho các bạn trong việc học tập và nâng cao kỹ năng giải toán về hình học.

Công thức tính diện tích của hình vuông một cách chính xác nhất

Khái niệm số thực và các dạng toán học phổ biến liên quan đến số thực