Đường trung tuyến

Đường trung tuyến của một đoạn thẳng là đường thẳng đi qua điểm giữa của đoạn thẳng đó.

Trong hình học, đường trung tuyến của một tam giác là đoạn thẳng kéo dài từ một đỉnh của tam giác đến điểm giữa của cạnh đối diện. Mỗi tam giác đều có ba đoạn trung tuyến.

Đối với tam giác cân và tam giác đều, mỗi đoạn trung tuyến sẽ chia đôi các góc ở đỉnh, tạo thành hai cạnh kề có chiều dài bằng nhau.

Trong không gian hình học, khái niệm tương tự là mặt trung tuyến trong tứ diện.

Đặc điểm của đường trung tuyến

Giao nhau tại một điểm

Ba đường trung tuyến của một tam giác giao nhau tại một điểm duy nhất, gọi là trọng tâm. Khoảng cách từ trọng tâm đến các đỉnh của tam giác bằng 2/3 chiều dài của đường trung tuyến tương ứng với đỉnh đó.

Phân chia diện tích thành các phần bằng nhau

Mỗi đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau. Ba đường trung tuyến chia tam giác thành sáu phần nhỏ, mỗi phần có diện tích tương đương.

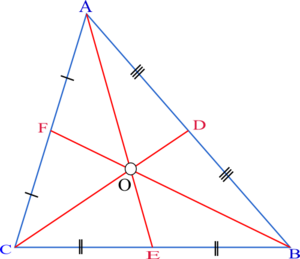
Xem xét tam giác ABC (như trong hình), với D là trung điểm của $\stackrel{¯<!--\; ¯\; -->}{AB}$, E là trung điểm của $\stackrel{¯<!--\; ¯\; -->}{BC}$, F là trung điểm của $\stackrel{¯<!--\; ¯\; -->}{AC}$, và O là trọng tâm của tam giác.

Theo định nghĩa, $AD=DB,AF=FC,BE=EC$. Do đó, các tam giác $\left[ADO\right]=\left[BDO\right],\left[AFO\right]=\left[CFO\right],\left[BEO\right]=\left[CEO\right],$ và $\left[ABE\right]=\left[ACE\right]$, với $\left[ABC\right]$ là diện tích của tam giác $\mathrm{△<!--\; △\; -->}ABC$; điều này đúng bởi trong mỗi trường hợp, hai tam giác có đáy bằng nhau và cùng đường cao từ đáy, vì vậy diện tích của chúng bằng nửa tích của đáy với chiều cao.

Ta có:

$\left[ABO\right]=\left[ABE\right]-<!--\; -\; -->\left[BEO\right]$

$\left[ACO\right]=\left[ACE\right]-<!--\; -\; -->\left[CEO\right]$

Vì vậy, $\left[ABO\right]=\left[ACO\right]$

{\displaystyle [ABO]=[ACO]\,} và $\left[ADO\right]=\left[DBO\right],\left[ADO\right]=\frac{1}{2}\left[ABO\right]$

Vì $\left[AFO\right]=\left[FCO\right],\left[AFO\right]=\frac{1}{2}ACO=\frac{1}{2}\left[ABO\right]=\left[ADO\right]$, ta có thể kết luận rằng $\left[AFO\right]=\left[FCO\right]=\left[DBO\right]=\left[ADO\right]$. Áp dụng cách này, ta có thể chứng minh rằng $\left[AFO\right]=\left[FCO\right]=\left[DBO\right]=\left[ADO\right]=\left[BEO\right]=\left[CEO\right]$.

Công thức liên quan đến độ dài của trung tuyến

Chiều dài của trung tuyến có thể được tính bằng định lý Apollonius như sau:

$m_c=\sqrt{\frac{2a^2+2b^2-<!--\; -\; -->c^2}{4}},$

Trong đó, a, b, và c là các cạnh của tam giác với các trung tuyến tương ứng m_a, m_b, và m_c nối từ các trung điểm.

Do đó, chúng ta có các mối liên hệ sau đây:

$a=\frac{2}{3}\sqrt{-<!--\; -\; -->m_a^2+2m_b^2+2m_c^2}=\sqrt{2(b^2+c^2)-<!--\; -\; -->4m_a^2}=\sqrt{\frac{b^2}{2}-<!--\; -\; -->c^2+2m_b^2}=\sqrt{\frac{c^2}{2}-<!--\; -\; -->b^2+2m_c^2\stackrel{¯<!--\; ¯\; -->}{},}$

• Đường cao trong tam giác
• Đường phân giác của tam giác
• Đường trung trực của tam giác

Chú thích

Liên kết

• Các đường trung tuyến và phân giác trong tam giác
• Đường trung tuyến tại cut-the-knot
• Diện tích của tam giác đường trung tuyến tại cut-the-knot
• Đường trung tuyến của tam giác với hoạt hình tương tác
• Hướng dẫn vẽ đường trung tuyến của tam giác bằng compa và thước kẻ với hoạt hình minh họa
• Weisstein, Eric W., 'Đường Trung Tuyến Tam Giác' từ MathWorld.