 Once you grasp the basics, factor trees become quite straightforward. damircudic / Getty Images
Once you grasp the basics, factor trees become quite straightforward. damircudic / Getty ImagesAs you progress in mathematics, you'll inevitably encounter the idea of factors. Although it might seem intimidating initially, especially if it's unfamiliar, you'll soon master the process of identifying all the factors for any given number.
Here, we'll focus on examining the factors of 36.
What Is a Factor?
In math, a factor refers to a number that divides another number evenly, leaving no remainder. Typically, you'll come across factors when given a specific number—whether by a teacher, in a homework assignment, on a test, or in a real-world scenario—and asked to identify all its factors.
Factors of 36
The factors of 36, listed in ascending order, are 1, 2, 3, 4, 6, 9, 12, 18, and 36. These are the only numbers that can divide 36 completely, resulting in whole numbers without any remainders.
That covers all the factors of 36! There are no additional factors, making this a perfect example to demonstrate how factors work. Factors can also be used or classified in various ways, offering multiple perspectives on their application.
Factors of 36: Examples of Factors at Work
Below are examples demonstrating how each factor of 36 operates:
36 ÷ 1 = 36
Here, we’re using the smallest and largest factors of 36. Dividing 36 by 1 yields 36, with no remainder, and returns the original number—an ideal starting point.
36 ÷ 2 = 18
When 36 is divided by 2, the result is 18. This division leaves no remainder, as 18 is exactly half of 36. Similarly, multiplying 18 by 2 brings us back to 36.
36 ÷ 3 = 12
Dividing 36 by 3 gives 12. Reversing the operation, multiplying 12 by 3 returns 36. Since there’s no remainder, 3 is confirmed as the third factor of 36.
36 ÷ 4 = 9
Dividing 36 by 4 results in 9. Naturally, multiplying 9 by 4 restores the original number, 36.
36 ÷ 6 = 6
Multiplying 6 by 6 results in 36, and dividing 36 by 6 gives 6. As expected, there are no remainders in this operation.
36 ÷ 9 = 4
This might feel familiar, and that’s a good sign! As previously shown, multiplying 4 by 9 equals 36, so dividing 36 by 4 naturally yields 9.
36 ÷ 12 = 3
We’re revisiting familiar territory here. Multiplying 12 by 3 gives 36, and dividing 36 by 12 returns 3.
36 ÷ 18 = 2
If this feels repetitive, that’s perfectly fine. Repetition in math aids memorization and deepens understanding. To ensure thoroughness, we’re highlighting that 18 fits into 36 exactly twice.
36 ÷ 36 = 1
We’ve come full circle! Any number divided by itself equals 1, which is why 36 is included as one of its own factors.
How to Determine the Factors of 36
Now that you’re familiar with the factors of 36 inside and out, you might feel confident about the concept. But what if you didn’t already know them? To identify factors from scratch, you’ll need to perform some division.
To find the factors of 36, divide it by every natural number from 1 to 9. Numbers like 1, 2, 3, and 4 will divide evenly into 36. However, when you reach 5, you’ll notice a remainder appears.
Multiplying 5 by 7 gives 35, which is the closest you can get to 36 without exceeding it. This leaves a remainder of 1, so 36 ÷ 5 = 7 with a remainder of 1.
Since 5 doesn’t divide evenly into 36, it’s not a factor. The same applies to 7 and 8. Through this basic division process, you’ve successfully identified all the factors of 36.
Positive and Negative Factor Pairs of 36
Another approach to listing factors is by organizing them into pairs. These pairs consist of numbers that, when multiplied together, result in 36.
Positive Factor Pairs
Having already identified all the factors of 36, we can now group them into pairs that, when multiplied, equal 36.
- 1 and 36 (1 x 36 = 36)
- 2 and 18 (2 x 18 = 36)
- 3 and 12 (3 x 12 = 36)
- 4 and 9 (4 x 9 = 36)
- 6 and 6 (6 x 6 = 36)
It’s worth noting that these factor pairs of 36 can also be reversed, such as 4 x 9 being the same as 9 x 4.
Negative Factor Pairs
Up until now, we’ve focused solely on the positive factors of 36. However, remember that multiplying two negative numbers yields a positive result. This means you can also identify negative factor pairs.
Therefore, the negative factors of 36 are essentially the opposites of the positive factor pairs. By converting each positive factor to its negative counterpart, you’ll have the complete list.
- -1 and -36 (-1 x -36 = 36)
- -2 and -18 (-2 x -18 = 36)
- -3 and -12 (-3 x -12 = 36)
- -4 and -9 (-4 x -9 = 36)
- -6 and -6 (-6 x -6 = 36)
What Are the Prime Factors of 36?
The prime factors of 36 are simply 2 and 3. That’s all there is to it.
However, it’s important to define our terms clearly, as prime factorization loses its meaning without understanding what prime numbers are.
A prime number is a natural number greater than 1 that cannot be evenly divided by any number other than itself and 1. Examples include 2, 3, 5, 7, and 11, among others.
It’s worth noting that the other factors of 36, which are not prime, are referred to as composite numbers. A composite number is defined as a number with more than two factors.
Having already identified the factors of 36, we now need to determine which of these factors are prime numbers. From the list of factors, it’s clear that only 2 and 3 qualify as prime factors.
Prime Factorization of 36
In addition to the comparison method we’ve discussed, there’s a specific step-by-step process for solving prime factorization.
- Start by dividing 36 by the smallest prime factor, which is 2: 36 ÷ 2 = 18.
- Next, divide 18 by 2. Continue this process until it’s no longer possible. Since 18 ÷ 2 = 9, we’re left with 9.
- At this point, 9 cannot be divided evenly by 2. Move to the next prime number, which is 3: 9 ÷ 3 = 3.
- Since 3 can only be divided by itself and 1, it’s a prime factor, and we’ve now reduced the problem to prime factors only.
- Thus, the prime factors of 36 are 2 and 3.
The prime factorization of 36 can be expressed as:
Alternatively, it can be expressed as:
In both representations, the prime factors of 36 are confirmed to be 2 and 3.
Factor Tree: Another Method for Prime Factorization
Another method to identify the prime factors of 36 is by using a factor tree. Factor trees provide a visual representation of the prime factorization process described earlier.
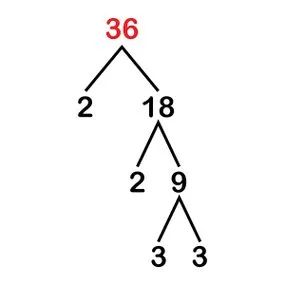 Prime factorization of 36.
zizou7 / Shutterstock
Prime factorization of 36.
zizou7 / ShutterstockTo create a factor tree, begin with the number 36. Then, follow the prime factorization steps detailed in the previous section. The process remains the same, but you’ll write each factor pair beneath the preceding numbers.
For example, 36 ÷ 2 = 18: You’ll write 2 and 18 below 36. Below 18, you’ll write 9 and 2. Below 9, you’ll write 3 and 3. This visual representation clearly displays the prime factors of 36.
Alternatively, you could divide 36 by other factors, like 4 and 9, and continue breaking them down until you identify all the prime factors. Regardless of the path you take, you’ll still arrive at the same prime factors for 36.
Common Factors
Another common math problem involves finding the common factors of two numbers. To solve this, we can apply the methods we’ve already discussed.
For instance, what are the shared factors of 36 and 14?
We already know the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. Using the same approach, we can determine that the factors of 14 are 1, 2, 7, and 14.
As a result, the shared factors of 36 and 14 are 1 and 2. These two numbers have only these two factors in common.
