Cách tỷ lệ tự nhiên có thể được áp dụng cho đầu tư

Melissa Ross / Getty Images
Tồn tại một tỷ lệ đặc biệt có thể được sử dụng để mô tả tỷ lệ của mọi thứ từ các khối xây dựng nhỏ nhất trong tự nhiên, như nguyên tử, đến các mẫu hình phức tạp nhất trong vũ trụ, như các hành tinh vô cùng lớn. Tự nhiên dựa vào tỷ lệ bẩm sinh này để duy trì sự cân bằng, nhưng thị trường tài chính cũng dường như tuân theo 'tỷ lệ vàng' này.
Tỷ lệ vàng được rút ra từ dãy Fibonacci, một chuỗi số mà mỗi số hạng là tổng của hai số hạng liền trước. Mặc dù chuỗi này được liên kết với Leonardo của Pisa, các số Fibonacci thực ra đã được sáng lập lần đầu tiên bởi nhà toán học Ấn Độ, Virahanka, cách đây 600 năm so với khi chúng được giới thiệu vào thế giới phương Tây.
Ở đây, chúng ta sẽ tìm hiểu về một số công cụ phân tích kỹ thuật đã được phát triển để tận dụng mẫu mực này.
Những điểm nhấn chính
- Tỷ lệ vàng là một số vô tỉ bằng (1+√5)/2, hoặc gần bằng 1,618...
- Tỷ lệ này được rút ra từ một công thức toán học cổ Ấn Độ mà xã hội phương Tây đặt tên cho Leonardo Fibonacci, người giới thiệu khái niệm này vào châu Âu.
- Thiên nhiên sử dụng tỷ lệ này để duy trì sự cân bằng, và thị trường tài chính cũng có vẻ thế.
- Dãy Fibonacci có thể được áp dụng vào tài chính bằng bốn kỹ thuật chính: phục hồi, cung đường, quạt và vùng thời gian.
- Số Fibonacci đã trở nên nổi tiếng trong văn hóa phổ thông, mặc dù một số chuyên gia cho rằng vai trò của chúng đã được phóng đại.
Lịch sử của Toán học
Các nhà toán học, nhà khoa học và nhà tự nhiên học đã biết về tỷ lệ vàng trong nhiều thế kỷ. Nó được rút ra từ dãy Fibonacci, được đặt theo tên nhà toán học Pisa Leonardo Fibonacci, người sống từ khoảng năm 1175 đến khoảng năm 1250.
Mặc dù Fibonacci giới thiệu những số này cho thế giới phương Tây, chúng thực ra đã được các nhà toán học Ấn Độ phát hiện ra hàng trăm năm trước. Nhà thơ Pingala đã sử dụng chúng để đếm số âm tiết trong thơ Sanskrit vào khoảng năm 200 trước Công nguyên, và phương pháp tính toán chúng đã được nhà toán học Ấn Độ Virahanka công thức hóa khoảng 800 năm sau đó.
Trong chuỗi này, mỗi số đơn giản là tổng của hai số liền trước (1, 1, 2, 3, 5, 8, 13, v.v.).
Fibonacci mượn nhiều từ các nguồn Ấn Độ và Ả Rập. Trong cuốn sách Liber Abaci, ông mô tả hệ thống số chữ số Hin-Ấn-A Rập biểu diễn bởi các số từ 0 đến 9. Ông gọi đây là 'Modus Indorum,' hoặc phương pháp của người Ấn Độ.
Nhưng chuỗi này không quá quan trọng. Phần quan trọng là khi các số càng lớn, thương của mỗi cặp số Fibonacci liên tiếp xấp xỉ 1,618, hoặc nghịch đảo của nó là 0,618. Tỉ lệ này được biết đến với nhiều tên gọi: tỉ lệ vàng, tỉ lệ vàng, ϕ và tỉ lệ thần thánh, trong số các tên khác.
Vậy tại sao con số này lại quan trọng? Có rất nhiều thứ trong tự nhiên có các tính chất chiều không gian tuân thủ tỉ lệ 1,618, vì vậy dường như nó có một chức năng cơ bản cho các khối xây dựng của tự nhiên.
Giá trị chính xác của tỉ lệ vàng có thể được tính bằng cách:
ϕ = (1+√5) / 2
Ví dụ về Tỉ lệ Vàng
Bạn không tin? Hãy xem ong mật, ví dụ. Nếu bạn chia số ong cái cho số ong đực trong bất kỳ tổ ong nào, bạn sẽ có một con số xung quanh 1,618. Hoa hướng dương, có các xoắn ốc hạt ngược nhau, có tỉ lệ 1,618 giữa đường kính của mỗi vòng quay. Cùng tỉ lệ này có thể được nhìn thấy trong các mối quan hệ giữa các thành phần khác nhau khắp tự nhiên.
Tỉ lệ vàng cũng xuất hiện trong nghệ thuật, bởi vì nó hấp dẫn hơn so với các tỉ lệ khác về mặt thẩm mỹ. Parthenon tại Athens, Kim tự tháp lớn tại Giza và Mona Lisa của Da Vinci đều tích hợp các hình chữ nhật có kích thước dựa trên tỉ lệ vàng. Dường như nó là không thể tránh khỏi.
Nhưng liệu điều đó có có ý nghĩa trong tài chính không? Thực tế, thị trường tài chính có cùng cơ sở toán học như các hiện tượng tự nhiên này. Bên dưới, chúng ta sẽ xem xét một số cách mà tỉ lệ vàng có thể được áp dụng vào tài chính, và chúng ta sẽ trình bày một số biểu đồ làm chứng minh.
Giao dịch và Đầu tư với Tỉ lệ Vàng
Tỉ lệ vàng thường được sử dụng bởi các nhà giao dịch và phân tích kỹ thuật, họ sử dụng nó để dự đoán các biến động giá cả được thúc đẩy bởi thị trường. Điều này bởi vì các số Fibonacci và tỉ lệ vàng có một ý nghĩa tâm lý mạnh mẽ trong hành vi bầy đàn. Các nhà giao dịch có khả năng lớn hơn để thu lợi nhuận hoặc phủ nhận các khoản lỗ tại các điểm giá cả nhất định, mà chính là được đánh dấu bởi tỉ lệ vàng.
Thú vị thay, việc sử dụng rộng rãi tỉ lệ vàng trong phân tích giao dịch hình thành một phép màu tự làm hiện thực: càng nhiều nhà giao dịch dựa vào chiến lược giao dịch dựa trên Fibonacci, thì các chiến lược đó sẽ có xu hướng hiệu quả hơn.
Nhờ những cuốn sách như The Da Vinci Code của Dan Brown, tỉ lệ vàng đã được nâng lên gần như là một thần thánh trong văn hóa phổ thông. Tuy nhiên, một số nhà toán học đã cho rằng sự quan trọng của tỉ lệ này đã được phóng đại quá mức.
Tỉ lệ Vàng và Phân Tích Kỹ Thuật
Khi được sử dụng trong phân tích kỹ thuật, tỉ lệ vàng thường được dịch thành ba phần trăm: 38,2%, 50%, và 61,8%. Tuy nhiên, có thể sử dụng nhiều bội số hơn khi cần thiết, như 23,6%, 161,8%, 423%, và cứ thế. Trong khi đó, có bốn cách mà dãy Fibonacci có thể được áp dụng vào biểu đồ: rút gọn, hình cung, quạt và múi giờ. Tuy nhiên, không phải tất cả đều có sẵn, phụ thuộc vào ứng dụng biểu đồ đang được sử dụng.
1. Rút Gọn Fibonacci
Rút gọn Fibonacci sử dụng các đường ngang để chỉ ra khu vực hỗ trợ hoặc kháng cự. Các mức được tính bằng cách sử dụng điểm cao và thấp của biểu đồ. Sau đó vẽ năm đường: đường đầu tiên tại 100% (cao nhất trên biểu đồ), đường thứ hai tại 61,8%, đường thứ ba tại 50%, đường thứ tư tại 38,2%, và đường cuối cùng tại 0% (thấp nhất trên biểu đồ). Sau một đợt biến động giá đáng kể lên hoặc xuống, các mức hỗ trợ và kháng cự mới thường nằm ở hoặc gần các đường này.
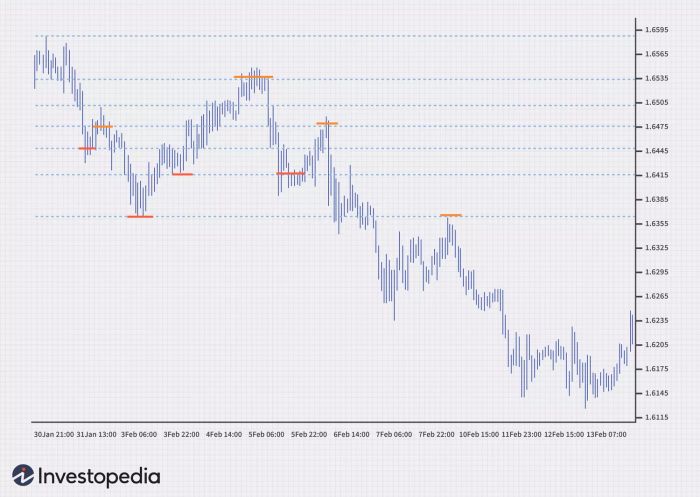
2. Cung Fibonacci
Tìm điểm cao và thấp của biểu đồ là bước đầu tiên để tạo nên các cung Fibonacci. Sau đó, với sự di chuyển giống như la bàn, ba đường cong được vẽ tại 38,2%, 50% và 61,8% từ điểm mong muốn. Những đường này dự đoán các mức hỗ trợ và kháng cự, cũng như các phạm vi giao dịch.
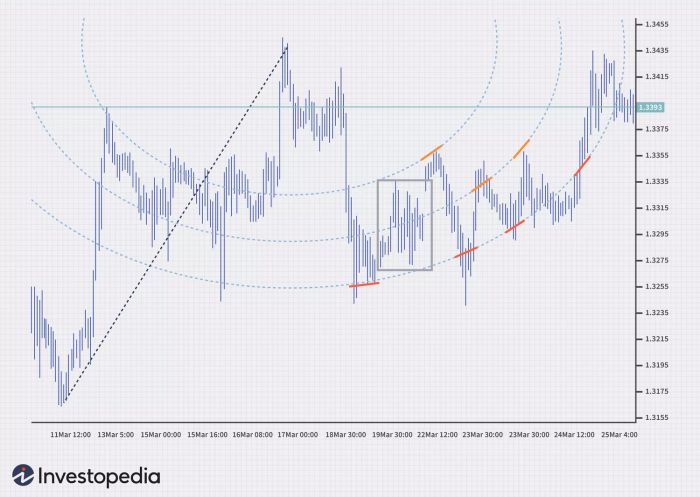
3. Các quạt Fibonacci
Các quạt Fibonacci bao gồm các đường chéo. Sau khi xác định cao điểm và thấp điểm của biểu đồ, một đường ngang vô hình được vẽ qua điểm phải nhất. Đường ngang vô hình này sau đó được chia thành 38,2%, 50% và 61,8%, và các đường được vẽ từ điểm trái nhất qua mỗi điểm này. Những đường này chỉ ra các khu vực hỗ trợ và kháng cự.
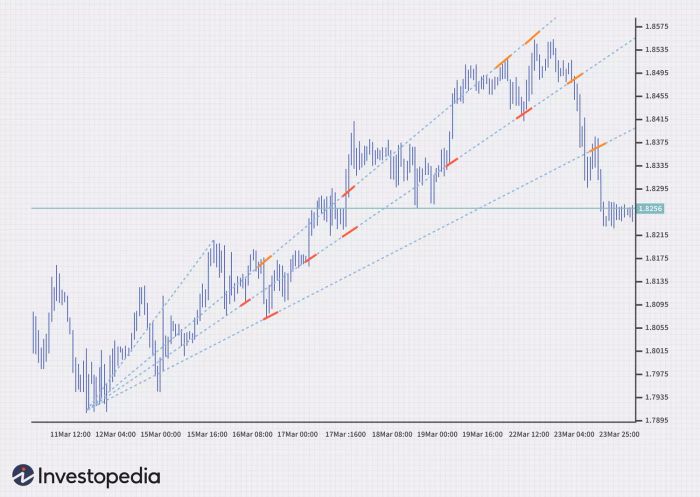
4. Các Khu vực Thời gian Fibonacci
Khác với các phương pháp Fibonacci khác, các khu vực thời gian là một loạt các đường dọc. Chúng được tạo thành bằng cách chia biểu đồ thành các đoạn với các đường dọc cách nhau theo chuỗi Fibonacci (1, 1, 2, 3, 5, 8, 13, vv). Mỗi đường chỉ ra một thời điểm mà có thể mong đợi diễn biến giá chính.
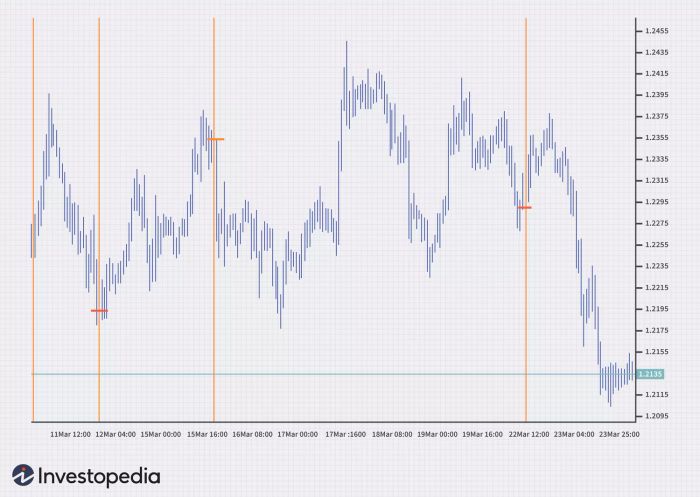
Mối Quan Hệ Giữa Dãy Fibonacci Và Tỷ Lệ Vàng Là Gì?
Tỷ lệ vàng được suy ra bằng cách chia mỗi số trong dãy Fibonacci cho số ngay trước nó. Theo thuật ngữ toán học, nếu F(n) mô tả số Fibonacci thứ n, thương F(n)/ F(n-1) sẽ tiến dần tới giới hạn 1.618... với các giá trị n ngày càng lớn. Giới hạn này được biết đến nhiều hơn với tên gọi là tỷ lệ vàng.
Tại sao Dãy Fibonacci Quan Trọng?
Dãy Fibonacci là một chuỗi số đệ quy trong đó mỗi giá trị được xác định bởi hai giá trị ngay trước nó. Vì lý do này, các số Fibonacci thường xuất hiện trong các vấn đề liên quan đến tăng trưởng dân số. Khi được sử dụng trong nghệ thuật thị giác, chúng cũng có tính thẩm mỹ, mặc dù ý nghĩa của chúng thường bị phóng đại quá mức trong văn hóa đại chúng.
Tại sao 1.618 Quan Trọng?
Số 1.61803... được biết đến nhiều hơn với tên gọi là tỷ lệ vàng, và thường xuất hiện trong nghệ thuật, kiến trúc và khoa học tự nhiên. Nó được suy ra từ dãy số Fibonacci, trong đó mỗi mục nhập được định nghĩa đệ quy bởi các mục nhập liền trước. Tỷ lệ vàng cũng được sử dụng trong phân tích kỹ thuật vì các nhà giao dịch có xu hướng cư xử theo cách dự đoán gần như các đường Fibonacci quan trọng về mặt tâm lý.
Kết Luận Cuối Cùng
Các nghiên cứu Fibonacci không được thiết kế để cung cấp các chỉ báo chính để định thời điểm vào và ra khỏi vị trí; tuy nhiên, các con số này hữu ích để ước tính các khu vực hỗ trợ và kháng cự. Nhiều người sử dụng sự kết hợp của các nghiên cứu Fibonacci để có dự báo chính xác hơn. Ví dụ, một nhà giao dịch có thể quan sát các điểm giao nhau trong một kết hợp của các hình cung Fibonacci và các mức kháng cự.
Các nghiên cứu Fibonacci thường được sử dụng phối hợp với các hình thức phân tích kỹ thuật khác. Ví dụ, các nghiên cứu Fibonacci, kết hợp với sóng Elliott, có thể được sử dụng để dự báo mức độ điều chỉnh sau các sóng khác nhau. Hy vọng bạn có thể tìm ra ứng dụng riêng của mình cho các nghiên cứu Fibonacci và thêm vào bộ công cụ đầu tư của mình.
