| Hình học |
|---|
Hình chiếu một mặt cầu lên mặt phẳng. |
|
|
Phân nhánh[hiện] |
|
Khái niệm[hiện] |
|
Không chiều[hiện] |
|
Một chiều[hiện] |
|
Hai chiều[hiện] |
|
Ba chiều[hiện] |
|
Bốn chiều / số chiều khác[hiện] |
| Nhà hình học |
|
theo tên[hiện] |
|
theo giai đoạn[hiện] |


Fractal, hay còn gọi là phân dạng, là một hình học có cấu trúc gấp khúc ở mọi tỷ lệ phóng đại, và có thể được phân tách thành các phần mà mỗi phần đều giống hình tổng thể nhưng ở tỷ lệ nhỏ hơn. Vì vậy, fractal có vô số chi tiết, với các chi tiết này có cấu trúc tự đồng dạng ở các tỷ lệ khác nhau. Thường thì fractal được tạo ra bằng cách lặp lại một mẫu toán học thông qua quy trình hồi quy. Thuật ngữ fractal lần đầu tiên được Benoît Mandelbrot sử dụng vào năm 1975, được lấy từ từ Latin fractus có nghĩa là 'bị vỡ'. Trước đó, các cấu trúc này (như bông tuyết Koch) được gọi là 'đường cong quái dị'.
Fractal ban đầu được nghiên cứu như một đối tượng toán học. Hình học fractal là lĩnh vực toán học chuyên tìm hiểu các thuộc tính của fractal, những thuộc tính mà hình học truyền thống không dễ dàng giải thích. Ngành này có ứng dụng trong khoa học, công nghệ và nghệ thuật máy tính. Ý tưởng chính của nó là phát triển các phương pháp đo lường mới về kích thước của đối tượng, bởi các phép đo thông thường trong hình học Euclid và giải tích không thể mô tả đầy đủ fractal.
Định nghĩa
Mặc dù việc định nghĩa các đặc tính của fractal có thể dễ dàng với trực quan, nhưng việc làm điều này một cách chính xác và cô đọng trong toán học lại là một thử thách lớn.
Mandelbrot định nghĩa fractal là 'một tập hợp mà số chiều Hausdorff (hoặc chiều Hausdorff-Besicovitch) lớn hơn số chiều tô pô học'. Chiều Hausdorff là một khái niệm dùng để đo kích thước của fractal, thường không phải là số nguyên. Một hình fractal trên mặt giấy hai chiều có thể bắt đầu thể hiện các đặc điểm của một đối tượng ba chiều và có thể có chiều Hausdorff nằm giữa 2 và 3. Đối với fractal hoàn toàn tự đồng dạng, chiều Hausdorff sẽ tương đương với chiều Minkowski-Bouligand.
Các vấn đề liên quan đến định nghĩa fractal bao gồm:
- Khái niệm 'gấp khúc' chưa được định nghĩa một cách chính xác.
- Không có định nghĩa thống nhất về 'chiều'.
- Có nhiều cách mà một đối tượng có thể thể hiện tính tự đồng dạng.
- Không phải tất cả fractal đều có thể được tạo ra bằng quy trình đệ quy.
Lịch sử
Các nhà toán học đã bắt đầu nghiên cứu các hình tự đồng dạng từ thế kỷ 17, khi Gottfried Leibniz xem xét các đường gấp khúc và định nghĩa đường thẳng như là một fractal tiêu chuẩn: 'các đường thẳng là đường cong, bất kỳ đoạn nào của nó đều giống như toàn bộ'.
Vào năm 1872, nhà toán học người Đức Karl Weierstrass giới thiệu một mô hình về một hàm liên tục nhưng không khả vi ở bất kỳ điểm nào.
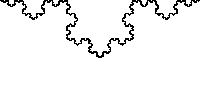
Vào năm 1904, nhà toán học Thụy Điển Helge von Koch trong bài viết 'Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire' đã nghiên cứu các đặc tính của fractal bắt nguồn từ các đa giác lồi phẳng, cụ thể là tam giác, có hình dáng tương tự như các cạnh của bông tuyết và được gọi là bông tuyết Koch (Koch snowflake).
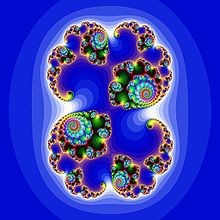
Tập hợp Mandelbrot

Tập Mandelbrot là tập hợp các điểm trong mặt phẳng phức, với biên của nó có dạng fractal. Tập Mandelbrot bao gồm các giá trị của số phức c mà quỹ đạo bắt đầu từ 0 dưới phép lặp của đa thức bậc hai với hệ số phức zn+1 = zn + c không vượt quá một giá trị xác định (giá trị này phụ thuộc vào c), bất kể n lớn như thế nào. Tập Mandelbrot được đặt theo tên nhà toán học Benoît Mandelbrot, người đầu tiên nghiên cứu và phát triển nó.
Chẳng hạn, với c = 1, khi áp dụng chuỗi lặp, ta nhận được dãy số 0, 1, 2, 5, 26,…, và dãy này tiến về vô cùng. Do đó, dãy này không bị chặn, và 1 không thuộc tập Mandelbrot.
Ví dụ khác, nếu ta chọn c = i (với i định nghĩa là i = −1), ta sẽ thu được dãy số 0, i, (−1 + i), −i, (−1 + i), −i,..., và vì dãy này bị chặn, nên i thuộc về tập Mandelbrot.
Khi được tính toán và vẽ trên mặt phẳng phức, tập Mandelbrot hiện lên với hình dạng fractal ở biên, và nó thể hiện tính tự đồng dạng khi được phóng đại ở bất kỳ điểm nào trên biên của tập hợp.
Tập Mandelbrot đã trở nên nổi tiếng không chỉ trong toán học mà còn bên ngoài lĩnh vực này, từ vẻ đẹp thẩm mỹ đến cấu trúc phức tạp xuất phát từ định nghĩa đơn giản, và nó là một trong những ví dụ nổi bật nhất về đồ họa toán học. Nhiều nhà toán học, bao gồm cả Mandelbrot, đã đưa lĩnh vực này đến với công chúng. Đây là một trong những tập fractal nổi tiếng nhất.
Ví dụ
Fractal được tạo ra từ hình học toán học




Các vật thể tự nhiên có cấu trúc fractal



Ứng dụng
Hình học fractal có nhiều ứng dụng trong cuộc sống, mở ra nhiều hướng nghiên cứu mới trong các lĩnh vực như sinh học, y học, thiên văn, kinh tế, và công nghệ thông tin...
Khoa học máy tính
Hình học fractal giúp thiết kế các hình ảnh đẹp trên máy tính một cách đơn giản và trực quan. Đây là một lĩnh vực thu hút nhiều sự quan tâm, đặc biệt từ những người yêu nghệ thuật. Cơ sở hình học fractal còn được ứng dụng hiệu quả trong công nghệ nén ảnh thông qua các hệ hàm lặp (IFS), một lĩnh vực mà các chuyên gia khoa học máy tính đặc biệt chú ý.
Phương pháp nén fractal là một kỹ thuật nén dữ liệu có mất mát thông tin cho ảnh số dựa trên fractal. Phương pháp này phù hợp nhất cho các ảnh tự nhiên do tính chất tự đồng dạng của các phần trong bức ảnh. Thuật toán fractal chuyển các phần này thành dữ liệu toán học gọi là 'mã fractal' để tái tạo lại bức ảnh đã được mã hóa. Đại diện của ảnh fractal được mô tả toán học như hệ thống các hàm lặp (IFS).
Với một ánh xạ co trên không gian metric đầy đủ, luôn tồn tại một điểm bất động. Khi mở rộng cho một họ các ánh xạ co, cũng chứng minh được sự tồn tại của điểm bất động. Điểm bất động có thể tìm được bằng cách lặp lại ánh xạ nhiều lần trên các kết quả thu được. Số lần lặp càng nhiều thì giá trị càng xấp xỉ chính xác điểm bất động. Nếu coi ảnh cần nén là 'điểm bất động' của một họ ánh xạ co thì chỉ cần lưu thông tin về họ ánh xạ đó, giúp giảm đáng kể dung lượng lưu trữ ảnh.
Y học và sinh học
Các nhà khoa học đã phát hiện mối quan hệ giữa fractal với hình dạng tế bào, quá trình trao đổi chất, ADN, nhịp tim,... Trước đây, các nhà sinh học cho rằng lượng chất trao đổi phụ thuộc vào khối lượng cơ thể người, tỉ lệ bậc 3 khi coi con người là đối tượng 3 chiều. Nhưng từ góc nhìn hình học fractal, chính xác hơn khi coi con người là một mặt fractal với số chiều xấp xỉ 2.5, tức tỉ lệ này là một số hữu tỷ. Việc chẩn đoán bệnh áp dụng hình học fractal đã có tiến bộ rõ rệt. Quan sát hình dạng tế bào theo quan điểm fractal giúp phát hiện bệnh lý, nhưng lĩnh vực này vẫn còn mới mẻ và cần được tiếp tục nghiên cứu.
Hóa học
Hình học fractal được ứng dụng trong nghiên cứu các hợp chất cao phân tử. Sự đa dạng về cấu trúc polymer thể hiện tính phong phú của các đặc tính fractal trong hợp chất cao phân tử. Hình dạng vô định hình, các đường nứt gãy, chuỗi, sự tiếp xúc của bề mặt polyme với không khí… đều liên quan đến fractal. Chuyển động của các phân tử, nguyên tử trong hợp chất, dung dịch và các quá trình tương tác gần giữa các chất cũng có thể xem như một hệ động lực hỗn độn (chaos).
Vật lý
Trong vật lý, khi nghiên cứu các hệ cơ học có năng lượng tiêu hao (chẳng hạn như có lực ma sát) người ta nhận thấy trạng thái của các hệ này khó dự đoán và hình ảnh hình học của chúng là các đối tượng fractal.
Thiên văn học
Các nhà khoa học đã nghiên cứu lại quỹ đạo của các hành tinh trong hệ mặt trời cũng như trong các hệ thiên hà khác. Kết quả cho thấy các hành tinh này không di chuyển theo quỹ đạo ellipse như trong hình học Euclid mà chuyển động theo các đường fractal. Quỹ đạo của chúng được mô phỏng bằng những quỹ đạo trong các tập hút 'lạ'.
Kinh tế
Sử dụng đồ hình fractal để mô tả sự biến động của giá cả trên thị trường chứng khoán cho phép chúng ta theo dõi và dự báo giá cả dựa trên các quy luật của hình học fractal.
Chú thích
- Fractal compression http://en.wikipedia.org/wiki/Fractal_compression
Liên kết ngoài
- Cổng thông tin Toán học
- Tư liệu liên quan tới Fractals tại Wikimedia Commons
- Fractal tại Encyclopædia Britannica (tiếng Anh)
- Fractal Geometry Lưu trữ 2007-10-07 tại Wayback Machine
- Ví dụ Mandelbox
- IFS Illusions - Nhân tạo nghệ thuật
| Tiêu đề chuẩn |
|
|---|
Bản mẫu: Lý thuyết hỗn loạn
Fractal | |
|---|---|
| Tính chất |
|
| Iterated function system |
|
| Strange attractor |
|
| L-system |
|
| Escape-time fractals |
|
| Rendering techniques |
|
| Random fractals |
|
| Nhân vật |
|
| Khác |
|
