Giả thuyết Goldbach được đưa ra bởi nhà toán học người Đức Christian Goldbach (1690-1764) vào năm 1742 trong một bức thư gửi cho Leonhard Euler. Đây là một trong những bài toán lâu đời và nổi tiếng vẫn chưa được giải quyết trong lý thuyết số cũng như trong toán học nói chung. Giả thuyết này dự đoán rằng:
- Mỗi số tự nhiên chẵn lớn hơn 2 có thể biểu diễn dưới dạng tổng của hai số nguyên tố.
Giả thuyết đã được xác nhận là đúng với các số lên tới 4 × 10, nhưng vẫn chưa có chứng minh hoàn chỉnh.
Lịch sử phát triển
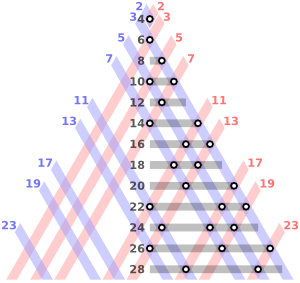
Giả thuyết đơn giản này được nhà toán học người Phổ thế kỷ 18, Goldbach, đề xuất. Theo đó, mỗi số chẵn lớn hơn 2 có thể được viết dưới dạng tổng của hai số nguyên tố, ví dụ như 4 = 2 + 2, 8 = 5 + 3, 20 = 13 + 7. Tuy nhiên, giả thuyết này chưa được chứng minh cho tất cả các số chẵn.
Trong thế kỷ 21, nhờ sự hỗ trợ của máy tính và các phần mềm tính toán hiện đại, các nhà nghiên cứu đã kiểm tra và xác nhận giả thuyết này là đúng cho các số chẵn đến giới hạn 4 tỷ tỷ (4 và 18 số 0).
Tài liệu tham khảo bên ngoài
- Hazewinkel, Michiel biên tập (2001), “Vấn đề Goldbach”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- Thư gốc của Goldbach gửi Euler — định dạng PDF (bằng tiếng Đức và Latin)
- Giả thuyết Goldbach, một phần của Prime Pages của Chris Caldwell.
- Xác minh giả thuyết Goldbach, tìm kiếm phân tán của Tomás Oliveira e Silva.
