Trong tài chính, giá trị hiện tại ròng (NPV) hoặc 'giá trị hiện tại ròng' (NPW) của một chuỗi các dòng tiền, cả vào và ra, được xác định là tổng của các giá trị hiện tại (PV) của các dòng tiền thuộc cùng một thực thể. Nếu tất cả các dòng tiền tương lai đều là dòng tiền vào (như phiếu giảm giá và gốc trái phiếu) và dòng tiền ra duy nhất là giá mua, thì NPV đơn giản là PV của dòng tiền tương lai trừ đi giá mua (tức là PV của chính nó). NPV là công cụ chính trong phân tích dòng tiền chiết khấu (DCF) và là phương pháp tiêu chuẩn để áp dụng giá trị thời gian của tiền trong việc đánh giá các dự án dài hạn. Nó được dùng trong lập ngân sách vốn và phổ biến trong kinh tế, tài chính, kế toán, để đo lường sự vượt quá hoặc thiếu hụt của dòng tiền so với giá trị hiện tại khi các chi phí tài chính đã được tính.
NPV của một chuỗi dòng tiền, với các dòng tiền vào và tỷ lệ chiết khấu hoặc đường cong chiết khấu, có thể được xác định trong phân tích DCF. Quy trình này liên quan đến việc sử dụng các dòng tiền và mức giá đầu vào, và tính toán tỷ lệ chiết khấu sao cho giá trị NPV bằng mức giá đã cho. Điều này được gọi là năng suất và được ứng dụng rộng rãi trong kinh doanh trái phiếu.
Công thức tính
Mỗi dòng tiền vào hoặc ra được chiết khấu về giá trị hiện tại (PV). Sau đó, tổng của các giá trị này được tính. Vì vậy, NPV là tổng của tất cả các giá trị hiện tại này.
tại đây
- 't' - khoảng thời gian của dòng tiền
- 'i' - tỷ lệ chiết khấu, tức là tỷ lệ lợi nhuận có thể kiếm được từ một khoản đầu tư trên thị trường tài chính có mức độ rủi ro tương tự; chi phí cơ hội của vốn
- - dòng tiền ròng (số tiền mặt, dòng vào trừ dòng ra) tại thời điểm 't'. Đối với mục đích giáo dục, thường được đặt ở bên trái số tiền để nhấn mạnh vai trò của nó như là một khoản đầu tư (trừ).
Kết quả của công thức này, khi nhân với tiền thuần hàng năm và dòng tiền, rồi trừ đi chi phí tiền mặt ban đầu, sẽ cho ra giá trị hiện tại. Tuy nhiên, nếu các dòng tiền không bằng nhau, thì công thức trước đó sẽ được sử dụng để xác định giá trị hiện tại của từng dòng tiền một cách riêng biệt. Mọi dòng tiền trong vòng 12 tháng sẽ không được chiết khấu cho mục đích NPV.
Các tỷ lệ chiết khấu
Tỷ lệ sử dụng để chiết khấu dòng tiền trong tương lai với giá trị hiện tại là một biến quan trọng của quá trình này.
Chi phí vốn bình quân gia quyền (sau thuế) của một công ty thường được sử dụng, nhưng nhiều người tin rằng nó là thích hợp để sử dụng tỉ lệ chiết khấu cao hơn để điều chỉnh cho rủi ro hoặc các yếu tố khác. Một tỷ lệ chiết khấu biến với tỷ lệ cao hơn áp dụng để rút tiền chảy xảy ra dọc theo khoảng thời gian có thể được sử dụng để phản ánh các đường cong lãi suất phí bảo hiểm cho món nợ dài hạn.
Một cách tiếp cận để lựa chọn các yếu tố tỷ lệ chiết khấu là để quyết định mức vốn cần thiết cho dự án có thể trở lại nếu đầu tư vào một liên doanh khác. Nếu, ví dụ, vốn cần thiết cho dự án có thể kiếm được năm phần trăm ở những nơi khác, sử dụng tỷ lệ chiết khấu trong tính toán NPV cho phép một so sánh trực tiếp được thực hiện giữa Dự án A và thay thế. Liên quan đến khái niệm này là sử dụng Tỷ lệ tái đầu tư của công ty. Tỷ lệ tái đầu tư có thể được định nghĩa là tỷ lệ lợi nhuận đầu tư của công ty trên trung bình. Khi phân tích các dự án trong một môi trường vốn hạn chế, nó có thể thích hợp để sử dụng tỷ lệ tái đầu tư chứ không phải là chi phí bình quân của công ty vốn là yếu tố giảm giá. Nó phản ánh chi phí cơ hội đầu tư, chứ không phải là chi phí có thể thấp hơn vốn.
Một NPV tính bằng cách sử dụng các tỉ lệ chiết khấu biến (nếu họ được biết đến trong thời gian đầu tư) tốt hơn phản ánh tình hình thực tế hơn một tính từ tỷ lệ chiết khấu liên tục cho toàn bộ thời hạn đầu tư. Hãy tham khảo bài viết hướng dẫn bằng văn bản của Samuel Baker để có mối quan hệ chi tiết giữa giá trị NPV và tỷ lệ chiết khấu.
Đối với một số nhà đầu tư chuyên nghiệp, các quỹ đầu tư cam kết để nhắm mục tiêu một tỷ lệ hoàn vốn nhất định. Trong trường hợp này, đó là tỷ lệ lợi nhuận nên được lựa chọn là tỷ lệ chiết khấu để tính NPV. Bằng cách này, một so sánh trực tiếp có thể được thực hiện giữa lợi nhuận của dự án và tỷ lệ hoàn vốn mong muốn.
Việc chọn tỷ lệ chiết khấu có thể phụ thuộc vào mục đích sử dụng của nó. Nếu chỉ để xác định xem dự án có tạo ra giá trị cho công ty hay không, việc sử dụng chi phí vốn bình quân của công ty có thể là lựa chọn hợp lý. Tuy nhiên, nếu cần quyết định giữa các lựa chọn đầu tư để tối đa hóa giá trị của công ty, tỷ lệ tái đầu tư của công ty có thể là sự lựa chọn tốt hơn.
Sử dụng tỷ lệ thay đổi theo thời gian, hoặc phân biệt các dòng tiền 'đảm bảo' với các dòng tiền 'rủi ro' có thể là phương pháp tinh vi hơn, nhưng ít được áp dụng trong thực tế. Việc điều chỉnh tỷ lệ chiết khấu để phản ánh rủi ro thường rất khó thực hiện (đặc biệt là trong môi trường quốc tế) và khó làm tốt. Một phương pháp thay thế là điều chỉnh dòng tiền cho các yếu tố rủi ro bằng cách sử dụng rNPV hoặc phương pháp tương tự, sau đó chiết khấu theo tỷ lệ của công ty.
NPV trong quyết định đầu tư
NPV phản ánh giá trị mà một dự án đầu tư có thể mang lại cho doanh nghiệp. Nếu là dương, điều đó cho thấy dự án tạo ra giá trị từ dòng tiền chiết khấu tại thời điểm t. Ngược lại, nếu là âm, dự án có dòng tiền giảm giá tại thời điểm 't'. Một dự án có NPV dương có thể được chấp nhận, nhưng không nhất thiết phải thực hiện vì NPV với chi phí vốn không bao gồm chi phí cơ hội, tức là so với các lựa chọn đầu tư khác. Trong lý thuyết tài chính, nếu có sự lựa chọn giữa hai phương án loại trừ lẫn nhau, lựa chọn có NPV cao hơn nên được ưu tiên.
| Nếu... | Nó có nghĩa là... | Thì... |
|---|---|---|
| NPV > 0 | Đầu tư này sẽ có thể thêm giá trị cho công ty | Dự án có thể được chấp nhận |
| NPV < 0 | Đầu tư này có thể làm giảm giá trị công ty | Dự án này nên bị từ chối |
| NPV = 0 | Đầu tư sẽ không đạt được cũng như không mất đi giá trị cho công ty | Chúng ta nên thờ ơ trong quyết định có chấp nhận hoặc từ chối dự án. Dự án này không có thêm giá trị tiền tệ. Quyết định nên dựa trên các tiêu chí khác, ví dụ như vị trí chiến lược hoặc các yếu tố khác không rõ ràng trong tính toán. |
Ví dụ minh họa
Công ty cần quyết định liệu có nên ra mắt một dòng sản phẩm mới hay không. Dòng sản phẩm mới sẽ cần chi phí khởi đầu, chi phí vận hành và dòng tiền trong hơn sáu năm. Dự án này sẽ yêu cầu một khoản đầu tư ngay lập tức (t = 0) là $100,000 (bao gồm máy móc và chi phí đào tạo). Dòng tiền ra cho các năm từ 1 đến 6 dự kiến là $5,000 mỗi năm, trong khi dòng tiền vào dự kiến là $30,000 mỗi năm trong các năm 1-6. Tất cả các dòng tiền được tính sau thuế và không có dòng tiền nào sau năm thứ 6. Tỷ lệ lợi nhuận yêu cầu là 10%. Giá trị hiện tại (PV) có thể được tính cho từng năm (bảng dưới đây không chính xác).
| Tháng | Dòng tiền | Giá trị hiện tại |
|---|---|---|
| T=0 | -100,000 | |
| T=1 | -49701.81818 | |
| T=2 | -32364.46281 | |
| T=3 | 2294.515402 | |
| T=4 | 4868.51991 | |
| T=5 | 16098.62714 | |
| T=6 | 16278.29919 | |
| T=7 | 23650.43135 | |
| T=8 | 35956.52284 | |
| T=9 | 19816.38532 | |
| T=10 | 29629.77288 | |
| T=11 | 46381.55871 | |
| T=12 | 52907.69139 |
Tổng hợp tất cả các giá trị hiện tại cho thấy giá trị hiện tại ròng là $8,881.52. Do NPV dương, việc đầu tư vào dự án là lựa chọn tốt hơn so với việc không làm gì cả. Công ty nên đầu tư vào dự án này nếu không có phương án thay thế có NPV cao hơn.
Công thức tương tự trong Excel là:
- NPV(tỷ lệ, thu nhập_ròng) + đầu_tư_cơ_bản
- PV(tỷ lệ, số_tháng, thu nhập_ròng_hàng_tháng)
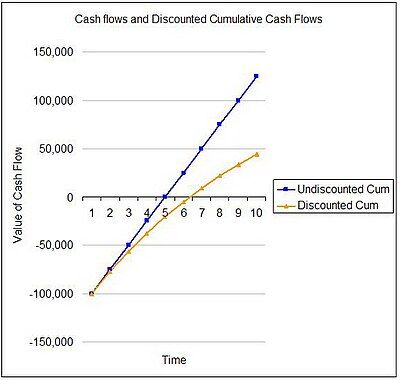
Trong thực tế, cần xem xét nhiều yếu tố khác như thuế, dòng tiền không đồng đều, giá trị còn lại và khả năng có các cơ hội đầu tư thay thế.
Các cạm bẫy thường gặp
- Nếu, chẳng hạn, nói chung là âm vào cuối dự án (ví dụ, một dự án công nghiệp hoặc khai thác có thể có chi phí làm sạch và phục hồi), thì công ty có thể mắc nợ tiền, do đó, tỷ lệ chiết khấu cao không phải là thận trọng mà là quá lạc quan. Đây là vấn đề với NPV. Một cách để giải quyết vấn đề này là cung cấp rõ ràng các khoản tài trợ cho bất kỳ tổn thất nào sau đầu tư ban đầu, tức là tính toán rõ ràng các chi phí tài chính như các tổn thất.
- Điều chỉnh rủi ro bằng cách thêm phí bảo hiểm vào tỷ lệ chiết khấu cũng là một cạm bẫy phổ biến. Mặc dù ngân hàng có thể tính lãi suất cao hơn cho một dự án rủi ro, điều đó không có nghĩa là cách tiếp cận này là hợp lệ để điều chỉnh giá trị hiện tại ròng đối với rủi ro, mặc dù nó có thể là một xấp xỉ hợp lý trong một số trường hợp. Nếu một số rủi ro dẫn đến tổn thất, thì một tỷ lệ chiết khấu trong NPV sẽ giảm tác động của tổn thất này thấp hơn so với chi phí tài chính thực tế. Cách tiếp cận hiệu quả hơn là xác định và đánh giá rủi ro rõ ràng, ví dụ, bằng cách tính toán bảo hiểm hoặc sử dụng kỹ thuật Monte Carlo, và tính toán rõ ràng chi phí tài chính cho bất kỳ tổn thất nào phát sinh.
- Một vấn đề khác liên quan đến việc ghép phí bảo hiểm rủi ro là R là sự kết hợp của tỷ lệ phi rủi ro và phí bảo hiểm rủi ro. Do đó, dòng tiền trong tương lai bị chiết khấu theo cả hai tỷ lệ phi rủi ro và phí bảo hiểm rủi ro, điều này làm phức tạp các kết quả vì mỗi dòng tiền tiếp theo đều bị ảnh hưởng. Điều này có thể dẫn đến NPV thấp hơn nhiều so với nếu tính toán theo cách khác. Mô hình Tương đương chắc chắn có thể được sử dụng để tính phí bảo hiểm rủi ro mà không làm phức tạp ảnh hưởng của nó lên giá trị hiện tại.
- NPV không cung cấp cái nhìn toàn diện về lợi ích hoặc tổn thất khi thực hiện một dự án. Để đánh giá tỷ lệ phần trăm lợi nhuận so với đầu tư cho dự án, thường sử dụng tỷ lệ hoàn vốn nội bộ hoặc các chỉ số hiệu quả khác như một bổ sung cho NPV.
- Người dùng không chuyên thường mắc lỗi khi tính NPV dựa trên dòng tiền sau lãi. Đây là sai lầm vì nó làm tăng gấp đôi giá trị thời gian của tiền. Dòng tiền tự do nên được sử dụng làm cơ sở tính toán NPV.
Lịch sử
Giá trị hiện tại ròng đã được sử dụng trong định giá ít nhất từ thế kỷ 19. Karl Marx đã đề cập đến NPV như là vốn hư cấu và tính toán này được gọi là 'tư bản hóa', và ông đã viết rằng:
Khái niệm vốn hư cấu, được gọi là tư bản hóa, xảy ra khi thu nhập định kỳ được xem như là khoản đầu tư bằng cách tính toán tỷ lệ lãi suất trung bình trên vốn đầu tư này.
Trong kinh tế học tân cổ điển, NPV đã được chính thức hóa và phổ biến bởi Irving Fisher trong cuốn sách năm 1907 của ông - 'Tỷ lệ lãi suất' và đã trở thành phần của sách giáo khoa tài chính từ những năm 1950 trở đi.
Các phương pháp lập ngân sách vốn thay thế
- Giá trị hiện tại điều chỉnh (APV): là giá trị hiện tại ròng của một dự án nếu chỉ được tài trợ bằng vốn chủ sở hữu cộng với giá trị hiện tại của tất cả các lợi ích tài chính.
- Tỷ lệ hoàn vốn kế toán (ARR): tỷ lệ tương tự như IRR và MIRR.
- Phân tích chi phí - lợi ích: xem xét các yếu tố khác ngoài tiền mặt, chẳng hạn như tiết kiệm thời gian.
- Tỷ lệ hoàn vốn nội bộ: tính toán tỷ lệ lợi nhuận của một dự án mà không cần quan tâm đến số tiền tuyệt đối cần đạt được.
- Tỷ lệ hoàn vốn nội bộ thay đổi (MIRR): tương tự như IRR, nhưng làm rõ các giả định về tái đầu tư dòng tiền. Đôi khi gọi là Tỷ lệ tăng trưởng của hoàn vốn.
- Thời gian hoàn vốn: đo lường thời gian cần thiết để các dòng tiền bằng với chi phí ban đầu. Đây là chỉ số về rủi ro, không phải hoàn vốn.
- Phương pháp Tùy chọn thực: cố gắng linh hoạt giá trị quản lý trong NPV.



Tài chính doanh nghiệp và ngân hàng đầu tư | |||||||
|---|---|---|---|---|---|---|---|
| Cơ cấu vốn | Nợ có bảo đám · Nợ cao cấp · Second lien debt · Subordinated debt · Nợ tầng lửng · Nợ chuyển đổi · Nợ xấu · Nợ trao đổi · Cổ phiếu ưu đãi · Warrant · Vay cổ đông · Cổ phiếu phổ thông · Pari passu | ||||||
| Các nghiệp vụ (điều kiện/điều khoản) |
| ||||||
| Định giá | Mô hình tài chính · Dòng tiền tự do · Định giá doanh nghiệp · Ý kiến công bằng · Định giá chứng khoán · APV · DCF · Giá trị hiện tại ròng (NPV) · Chi phí vốn (Chi phí vốn bình quân gia quyền) · Phân tích công ty có thể so sánh · Phân tích đậm đặc/pha loãng · Giá trị xí nghiệp · Lá chắn thuế · Lợi nhuận tối thiểu · Công ty phụ trợ · EVA · MVA · Giá trị giới hạn · Định giá các quyền chọn thực | ||||||
Danh sách ngân hàng đầu tư · Danh sách chủ đề tài chính | |||||||
