1. Các kiến thức cần nắm vững
1.1. Định nghĩa phân số
- Phân số bao gồm tử số và mẫu số. Tử số là số tự nhiên viết trên dấu gạch ngang, còn mẫu số là số tự nhiên khác 0 viết dưới dấu gạch ngang.
- Cách đọc phân số: khi đọc phân số, ta đọc tử số trước, sau đó nói 'phần' và cuối cùng là mẫu số.
Ví dụ: Phân số 1 / 8 được đọc là một phần tám
- Phân số có thể được sử dụng để biểu diễn kết quả của phép chia giữa một số tự nhiên với một số tự nhiên khác 0, và phân số đó gọi là thương của phép chia.
Ví dụ: 3 chia 5 = 3 / 5
- Mọi số tự nhiên có thể được biểu diễn dưới dạng phân số với mẫu số là 1.
Ví dụ: 6 = 6 / 1; 18 = 18 / 1; và nhiều ví dụ khác.
- Số 1 có thể được biểu diễn dưới dạng phân số với tử số và mẫu số bằng nhau và khác 0.
Ví dụ: 1 = 6 / 6; 1 = 18 / 18; và các ví dụ khác.
- Số 0 có thể được viết thành phân số với tử số là 0 và mẫu số khác 0.
Ví dụ: 0 = 0 / 8; 0 = 0 / 445; và nhiều ví dụ khác.
1.2. Các tính chất cơ bản của phân số
- Khi nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0, phân số mới vẫn giữ giá trị như phân số ban đầu.
- Khi chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0, phân số mới vẫn có giá trị bằng phân số gốc.
Ví dụ: 3 / 4 = (3 x 2) / (4 x 2) = 6 / 8; 12 / 20 = (12 / 4) / (20 / 4) = 3 / 5
1.3. Ứng dụng của các tính chất cơ bản của phân số
Dạng 1: Rút gọn phân số
Bước 1: Kiểm tra xem tử số và mẫu số của phân số có chia hết cho một số tự nhiên nào lớn hơn 1 không.
Bước 2: Chia cả tử số và mẫu số của phân số cho số tự nhiên đó.
Bước 3: Tiếp tục thực hiện như vậy cho đến khi phân số không còn có thể rút gọn thêm.
Chú ý: Phân số tối giản là phân số mà tử số và mẫu số không còn chia hết cho bất kỳ số nào lớn hơn 1.
Ví dụ: 9 / 15 = (9 / 3) / (15 / 3) = 3 / 5
Dạng 2: Quy đồng mẫu số các phân số
a) Trường hợp mẫu số chung là tích của hai mẫu số của các phân số đã cho
Bước 1: Nhân cả tử số và mẫu số của phân số đầu tiên với mẫu số của phân số thứ hai.
Bước 2: Nhân cả tử số và mẫu số của phân số thứ hai với mẫu số của phân số đầu tiên.
Ví dụ: Quy đồng mẫu số của hai phân số: 3 / 4 và 7 / 3
Mẫu số chung: 12
3 / 4 = (3 x 3) / (4 x 3) = 9 / 12
7 / 3 = (7 x 4) / (3 x 4) = 28 / 12
b) Khi mẫu số của một phân số chia hết cho mẫu số của các phân số còn lại
Bước 1: Chọn mẫu số chung là số chia hết cho mẫu số của tất cả các phân số còn lại
Bước 2: Tính thừa số phụ cần thiết
Bước 3: Nhân cả tử số và mẫu số của các phân số còn lại với thừa số phụ tương ứng
Bước 4: Giữ nguyên phân số có mẫu số đã chia hết cho mẫu số của các phân số còn lại
Ví dụ: Quy đồng mẫu số của hai phân số 15 / 16 và 3 / 8
Mẫu số chung = 16
15 / 16 = 15 / 16
3 / 8 = (3 x 2) / (8 x 2) = 6 / 16
1.4. So sánh hai phân số
* So sánh các phân số có cùng mẫu số
Quy tắc: Đối với các phân số có cùng mẫu số:
- Phân số có tử số nhỏ hơn sẽ nhỏ hơn phân số có tử số lớn hơn
- Phân số có tử số lớn hơn sẽ lớn hơn phân số có tử số nhỏ hơn
- Nếu tử số của hai phân số bằng nhau, thì hai phân số đó cũng bằng nhau
Ví dụ: 2 / 5 < 3 / 5; 3 / 5 > 2 / 5; 2 / 5 = 2 / 5
* So sánh hai phân số có cùng tử số
Quy tắc: Đối với các phân số có cùng tử số:
- Phân số có mẫu số nhỏ hơn sẽ lớn hơn phân số có mẫu số lớn hơn
- Phân số có mẫu số lớn hơn sẽ nhỏ hơn phân số có mẫu số nhỏ hơn
- Nếu hai phân số có cùng mẫu số, chúng sẽ bằng nhau
Ví dụ:
1 / 2 > 1 / 4; 2 / 5 < 2 / 3; 5 / 6 = 5 / 6
Lưu ý: Khi so sánh các phân số cùng tử số, học sinh thường bị nhầm lẫn. Hãy ghi nhớ và áp dụng đúng quy tắc.
a) Quy đồng mẫu số:
Quy tắc: Để so sánh hai phân số có mẫu số khác nhau, ta quy đồng mẫu số của chúng rồi so sánh tử số của các phân số đã quy đồng.
Phương pháp giải:
Bước 1: Quy đồng mẫu số cho hai phân số
Bước 2: So sánh hai phân số có cùng mẫu số
Bước 3: Đưa ra kết luận dựa trên so sánh
Ví dụ: So sánh hai phân số 2 / 3 và 3 / 4
Cách giải: 2 / 3 = 2 x 4 / 3 x 4 = 8 / 12
3 / 4 = 3 x 3 / 4 x 3 = 9 / 12
So sánh: 8 / 12 < 9 / 12 (vì 8 < 9)
Kết luận: 2 / 3 < 3 / 4
b) Quy đồng tử số:
- Khi hai phân số có mẫu số khác nhau nhưng một mẫu số rất lớn và tử số nhỏ, ta nên sử dụng phương pháp quy đồng tử số để đơn giản hóa việc tính toán.
- Quy tắc: Để so sánh hai phân số với tử số khác nhau, ta có thể quy đồng tử số của chúng rồi so sánh các mẫu số của hai phân số mới.
Phương pháp giải:
Bước 1: Quy đồng tử số cho hai phân số
Bước 2: So sánh hai phân số có tử số giống nhau.
Bước 3: Đưa ra kết luận cuối cùng.
Ví dụ: So sánh các phân số: 2 / 125 và 3 / 187.
Cách giải:
Ta có: 2 / 125 = 2 x 3 / 125 x 3 = 6 / 375.
3 chia 187 bằng 3 nhân 2 chia (187 nhân 2), tức là 6 chia 374
Vì 374 nhỏ hơn 375 nên 6 chia 374 lớn hơn 6 chia 375
1.5. Cộng và trừ các phân số
* Cộng và trừ các phân số có cùng mẫu số:
- Quy tắc: Để cộng (hoặc trừ) hai phân số có cùng mẫu số, ta chỉ cần cộng (hoặc trừ) hai tử số và giữ nguyên mẫu số.
Lưu ý: Sau khi thực hiện phép cộng (hoặc trừ) các phân số, nếu kết quả chưa được tối giản, hãy rút gọn để có phân số tối giản nhất.
* Cộng hoặc trừ các phân số có mẫu số khác nhau:
- Quy tắc: Để cộng (hoặc trừ) hai phân số có mẫu số khác nhau, trước tiên cần quy đồng mẫu số của chúng rồi thực hiện phép cộng (hoặc trừ) trên các phân số đã được quy đồng.
* Tính chất của phép cộng phân số
- Tính chất giao hoán: Khi thay đổi vị trí của các phân số trong một tổng, tổng của chúng vẫn không thay đổi.
- Tính chất kết hợp: Khi cộng tổng của hai phân số với một phân số thứ ba, bạn có thể cộng phân số đầu tiên với tổng của hai phân số còn lại.
- Cộng với 0: Khi cộng bất kỳ phân số nào với 0, kết quả sẽ là chính phân số đó.
Lưu ý: Các tính chất của phép cộng phân số thường được áp dụng trong các bài toán tính nhanh.
1.6. Phép nhân và phép chia phân số
* Phép nhân hai phân số và các tính chất của phép nhân phân số
a) Phép nhân hai phân số:
- Quy tắc: Để nhân hai phân số, ta nhân tử số với tử số và mẫu số với mẫu số.
- Lưu ý: Sau khi thực hiện phép nhân hai phân số, nếu kết quả chưa được tối giản, cần rút gọn phân số. Nên thực hiện việc rút gọn ngay sau khi nhân tử số và mẫu số, thay vì nhân xong rồi mới rút gọn.
b) Các tính chất của phép nhân phân số
- Tính chất giao hoán: Khi thay đổi vị trí của các phân số trong một tích, tích của chúng vẫn không thay đổi.
- Tính chất kết hợp: Khi nhân một tích của hai phân số với một phân số thứ ba, bạn có thể nhân phân số đầu tiên với tích của hai phân số còn lại.
- Tính chất phân phối: Khi nhân tổng của hai phân số với một phân số thứ ba, bạn có thể nhân từng phân số trong tổng với phân số thứ ba rồi cộng tất cả các kết quả lại.
- Nhân với số 1: Bất kỳ phân số nào nhân với 1 đều giữ nguyên giá trị của phân số đó.
Lưu ý: Các tính chất của phép nhân phân số thường được áp dụng trong các bài toán tính nhanh.
* Phép chia hai phân số:
a) Phân số nghịch đảo: Phân số nghịch đảo của một phân số là phân số mà tử số và mẫu số được hoán đổi cho nhau.
b) Phép chia phân số:
- Quy tắc: Để chia một phân số cho một phân số khác, ta nhân phân số đầu tiên với phân số nghịch đảo của phân số thứ hai.
1.7. Phân số thập phân
- Khái niệm: Phân số có mẫu số là 10, 100, 1000, v.v. được gọi là phân số thập phân.
Chú ý: Một số phân số có thể được chuyển đổi thành phân số thập phân.
1.8. Hỗn số
- Khái niệm: Hỗn số bao gồm phần nguyên và phần phân số.
- Các bước đọc hỗn số:
+ Bước 1: Đọc phần nguyên trước.
+ Bước 2: Đọc từ 'và'
+ Bước 3: Đọc phần phân số
- Cách chuyển đổi hỗn số thành phân số:
- Để chuyển đổi hỗn số thành phân số, thực hiện các bước sau:
+ Bước 1: Nhân phần nguyên với mẫu số, sau đó cộng với tử số.
+ Bước 2: Sử dụng kết quả từ bước 1 làm tử số mới, giữ nguyên mẫu số. Bạn sẽ có phân số mới chuyển từ hỗn số đã cho.
- Cách chuyển phân số thành hỗn số:
Để chuyển đổi một phân số thành hỗn số, làm theo các bước sau:
+ Bước 1: Chia tử số cho mẫu số.
+ Bước 2: Phần nguyên là kết quả của phép chia và sẽ là phần nguyên trong hỗn số.
+ Bước 3: Phần phân số là tử số mới trong hỗn số
+ Bước 4: Mẫu số giữ nguyên giá trị như cũ
- Phép tính với hỗn số:
+ Giống như phân số, hỗn số có thể thực hiện các phép toán cộng, trừ, nhân, chia với nhau.
+ Để thực hiện phép cộng hoặc trừ với hỗn số, bạn có thể làm theo một trong hai cách sau:
Cách 1: Chuyển hỗn số thành phân số và sau đó thực hiện các phép toán trên phân số.
Cách 2: Tách phần nguyên ra để thực hiện phép cộng hoặc trừ, và làm tương tự với phần phân số.
+ Để thực hiện phép nhân hoặc chia với hỗn số, trước tiên chuyển đổi hỗn số thành phân số rồi tiến hành các phép toán nhân chia trên phân số.
2. Giải bài tập Toán lớp 5: Ôn tập chung chương 1
Bài 1. Sắp xếp các phân số sau theo thứ tự từ lớn đến nhỏ
a) 9/25; 12/25; 7/25; 4/25; 23/25
b) 7/8; 7/11; 7/10; 7/9; 7/15
c) 2/3; 5/6; 7/9; 5/18
Cách giải:
- Trong hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn
- Khi so sánh hai phân số có cùng tử số, phân số có mẫu số nhỏ hơn sẽ lớn hơn.
- Để so sánh các phân số với mẫu số khác nhau, ta cần quy về cùng mẫu số rồi thực hiện so sánh.
Chi tiết cách giải:
a) Sắp xếp: 23/25 > 12/25 > 9/25 > 7/25 > 4/25
Vậy thứ tự các phân số từ lớn đến nhỏ là: 23/25; 12/25; 9/25; 7/25; 4/25
Ta có dãy phân số sau: 7 / 8 > 7 / 9 > 7 / 10 > 7 / 11 > 7 / 15
Do đó, thứ tự các phân số từ lớn đến nhỏ là: 7 / 8 ; 7 / 9 ; 7 / 10 ; 7 / 11 ; 7 / 15
c) Đồng nhất mẫu số (MSC = 18)
2 / 3 tương đương với 12 / 18
5 / 6 tương đương với 15 / 18
7 / 9 tương đương với 14 / 18
Phân số 5 / 18 giữ nguyên
Dãy phân số là: 15 / 18 > 14 / 18 > 12 / 18 > 5 / 18
Theo thứ tự từ lớn đến nhỏ, các phân số là: 5 / 6 ; 7 / 9 ; 2 / 3 ; 5 / 18
Bài 2. Tính toán
a) Tính tổng: 1 / 4 + 3 / 8 + 5 / 16 = ......
b) Tính hiệu: 3 / 5 - 1 / 3 - 1 / 6 = ......
c) Tính tích: 4 / 7 x 5 / 8 x 7 / 12 = ......
d) Tính thương: 25 / 28 : 15 / 14 x 6 / 7 = .....
Hướng dẫn giải:
- Để thực hiện phép cộng (hoặc trừ) nhiều phân số, ta cần quy đồng mẫu số của tất cả các phân số trước, sau đó mới thực hiện phép cộng (hoặc trừ).
- Để nhân các phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
- Để chia hai phân số, ta nhân phân số thứ nhất với phân số thứ hai sau khi đảo ngược phân số thứ hai.
Chi tiết giải bài toán:
a) 1 / 4 + 3 / 8 + 5 / 16 = 4 / 16 + 6 / 16 + 5 / 16 = (4 + 6 + 5) / 16 = 15 / 16
b) 3 / 5 - 1 / 3 - 1 / 6 = 18 / 30 - 10 / 30 - 5 / 30 = (18 - 10 - 5) / 30 = 3 / 30 = 1 / 10
c) 4 / 7 x 5 / 8 x 7 / 12 = (4 x 5 x 7) / (7 x 8 x 12) = 5 / (12 x 2) = 5 / 24
d) 25 / 28 : 15 / 14 x 6 / 7 = 25 / 28 x 14 / 15 x 6 / 7 = (25 x 14 x 6) / (28 x 15 x 7) = (5 x 5 x 14 x 2 x 3) / (14 x 2 x 5 x 3 x 7) = 5 / 7
Bài 3. Năm nay, tuổi của mẹ gấp ba lần tuổi của con. Tính tuổi của mỗi người biết rằng mẹ lớn hơn con 28 tuổi.
Phương pháp giải: Xác định tuổi của mẹ và con dựa trên tổng tuổi và tỷ số tuổi của hai người.
Chi tiết giải đáp:
Dưới đây là sơ đồ:
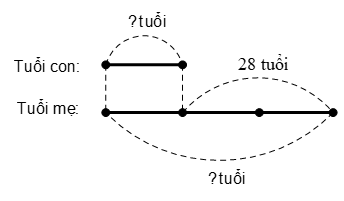
- Dựa trên sơ đồ, hiệu số các phần bằng nhau là:
3 - 1 = 2 (phần)
Tuổi của con là: 28 chia 2 x 1 = 14 (tuổi)
Tuổi của mẹ là: 14 x 3 = 42 (tuổi)
Kết quả: 14 x 3 = 42 tuổi
Bài 4. Nếu 3 / 5 diện tích trồng nhãn của xã là 6 ha, diện tích toàn xã trồng nhãn là bao nhiêu mét vuông?
Hướng dẫn giải:
- Để tính diện tích trồng nhãn, ta chia 6 ha cho 3 / 5 hoặc chia 6 ha cho 3 rồi nhân với 5
- Chuyển đổi ha sang mét vuông, với 1 ha = 10.000 m².
Chi tiết lời giải:
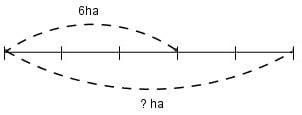
Phương pháp 1:
Diện tích trồng nhãn của xã này là:
6 chia 3 nhân 5 bằng 10 (ha)
10 ha tương đương với 100000 (m2)
Cách tính thứ hai: Diện tích trồng nhãn của xã là:
6 chia 3 nhân 5 bằng 10 (ha)
10 ha tương đương với 100.000 (m2)
Kết quả: 100000 m2
