1. Giải bài Toán lớp 6, bài 17 về Phép chia hết
1.1 Những kiến thức cơ bản về phép chia hết

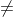
Nếu tồn tại một số nguyên q sao cho a = bq thì phép chia a : b sẽ cho thương là q.
Trong đó:
- a là số bị chia trong phép chia
- b là số chia trong phép chia
- q là kết quả của phép chia
Một số ví dụ minh họa:
a) 462 chia cho (-14) = - (462 chia cho 14) = -33
b) (-480) chia cho (-12) = 480 chia cho 12 = 40
c) (-176) chia cho 2 = - (176 chia cho 2) = 88
1.2 Đề bài Toán lớp 6 bài 17 Phép chia hết - sách Kết nối tri thức
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Bài luyện tập 1 trang 73
Bài 1: Thực hiện phép chia 135 chia cho 9. Từ đó, xác định thương của các phép chia 135 chia cho (-9) và (-135) chia cho (-9)
Bài 2: Tính toán các phép chia sau:
a) (-63) chia cho 9 b) (-24) chia cho (-8).
1.3 Đáp án
Bài 1:
135 chia cho 9 bằng 15
Vậy thương của các phép chia được tính như sau:
135 chia cho (-9) = - (135 chia cho 9) = -15
(-135) chia cho (-9) = 135 chia cho 9 = 15
Bài 2:
a) (-63) chia cho 9 = - (63 chia cho 9) = -7
b) (-24) chia cho (-8) = 24 chia cho 8 = 3
2. Giải Toán lớp 6 bài 17: ước và bội của một số nguyên
2.1 Kiến thức cơ bản về ước và bội của một số nguyên

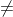
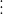
- Để xác định các ước của một số nguyên a bất kỳ, ta cần xét các ước nguyên dương của a cùng với số âm của chúng.
- Các ước của số nguyên âm a (-a) chính là các ước của số nguyên dương a (a).
Chú ý:
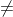
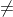
Ví dụ cụ thể:
+ Các bội của số 2 bao gồm 0, -2, 2, -4, 4, -6, 6, -8, 8, và các số tiếp theo.
+ Các ước của số 6 là: -1, 1, -2, 2, -3, 3, -6, và 6.
Về các đặc điểm:
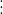
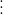
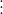 Ví dụ như sau:
Ví dụ như sau: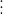
 Ví dụ minh họa:
Ví dụ minh họa:
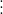
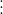
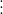 Ví dụ minh họa:
Ví dụ minh họa: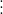
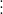
![\left [ 12 + (-6) \right ]](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479296ouW/anh-mo-ta.png)
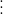
![\left [ 12 - (-6) \right ]](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479296oZP/anh-mo-ta.png)
2.2 Đề bài Toán lớp 6 bài 17 về ước và bội của một số nguyên - sách Kết nối tri thức
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Bài tập 2 trang 73
a) Xác định các ước của số -9
b) Tìm các bội của số 4 nằm trong khoảng từ -20 đến 20
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Câu 3.39 trang 74
Tính các kết quả của phép chia sau:
a) 297 chia cho (-3)
b) (-396) chia cho (-12)
c) (-600) chia cho 15
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Câu 3.40 trang 74
a) Xác định các ước của các số: 30, 42, và -50
b) Tìm những ước chung của 30 và 42
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Câu 3.41 trang 74
Liệt kê các phần tử của các tập hợp sau:
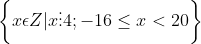
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Câu 3.42 trang 74
Tìm hai ước của số 15 mà tổng của chúng là -4
Toán lớp 6 Tập 1 - sách Kết nối tri thức: Câu 3.43 trang 74
Giải thích lý do: Nếu hai số đều chia hết cho -3 thì tổng và hiệu của chúng cũng chia hết cho -3. Thử nêu một kết luận tổng quát.
2.3 Đáp án
Hướng dẫn giải bài 3.39 trang 74 trong sách Toán lớp 6 Tập 1 - Kết nối tri thức
a) 297 chia cho (-3) = - (297 chia 3) = -99
b) (-396) chia cho (-12) = 396 chia 12 = 33
c) (-600) chia cho 15 = - (600 chia 15) = -40
Hướng dẫn giải bài 3.40 trang 74 trong sách Toán lớp 6 Tập 1 - Kết nối tri thức
a) Các ước của số 30 bao gồm: -1, 1, -2, 2, -3, 3, -5, 5, -6, 6, -10, 10, -15, 15, -30, 30.
Các ước của số 42 bao gồm: -1, 1, -2, 2, -3, 3, -6, 6, -7, 7, -14, 14, -21, 21, -42, 42.
Các ước của số -50 bao gồm: -1, 1, -2, 2, -5, 5, -10, 10, -25, 25, -50, 50.
b) Các ước chung của 30 và 42 là: -1, 1, -2, 2, -3, 3, -6, 6.
Hướng dẫn giải bài 3.41 trang 74 trong sách Toán lớp 6 Tập 1 - Kết nối tri thức
Vì x là số nguyên chia hết cho 4, nên x chính là bội của 4.
Để xác định các bội của 4, ta nhân các số 0, 1, 2, 3, 4, 5, 6, 7, ... với 4. Kết quả là các bội dương của 4: 0, 4, 8, 12, 16, 20, 24, 28, ...
Vậy các bội của 4 bao gồm: ...; -28; -24; -20; -16; -12; -8; -4; 0; 4; 8; 12; 16; 20; 24; 28; ...
Dựa theo yêu cầu, các bội của 4 nằm trong khoảng từ -16 đến dưới 20 là: -16, -12, -8, -4, 0, 4, 8, 12, 16.
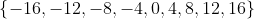
Hướng dẫn giải bài 3.42 trang 74 trong Toán lớp 6 Tập 1 - sách Kết nối tri thức
Các ước của số 15 bao gồm: -1, 1, -3, 3, -5, 5, -15, 15
Hai ước của số 15 có tổng bằng -4 là -5 và 1.
Hướng dẫn giải bài 3.43 trang 74 trong Toán lớp 6 Tập 1 - sách Kết nối tri thức
Giả sử a và b là hai số nguyên đều chia hết cho -3. Ta có thể viết a = (-3) . m và b = (-3) . n, với m và n là các số nguyên.
Tổng của hai số nguyên a và b được tính như sau: a + b = (-3).m + (-3).n = (-3) . (m + n)
Hiệu của hai số nguyên a và b là:
Hiệu của hai số nguyên a và b được tính như sau: a - b = (-3).m - (-3).n = (-3) . (m - n)
Do đó, nếu hai số đều chia hết cho -3, thì cả tổng và hiệu của chúng cũng sẽ chia hết cho -3.
Chúng ta có thể chứng minh điều này như sau:
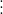
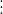
Từ đó ta có a + b = c.m + c.n = c. (m + n)
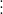
![\left [ c. (m + n) \right ]](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479296DIN/anh-mo-ta.png)