Giải chi tiết bài tập về đường vuông góc và đường xiên
Câu 1: Chọn phát biểu sai trong số các phát biểu dưới đây:
A. Khi kẻ đường từ một điểm ngoài một đường thẳng đến đường thẳng đó, thì đường vuông góc là đoạn đường ngắn nhất trong các đường xiên và đường vuông góc.
B. Trong hai đường xiên từ một điểm ngoài một đường thẳng đến đường thẳng đó, đường xiên có hình chiếu dài hơn sẽ dài hơn.
C. Trong hai đường xiên từ một điểm ngoài một đường thẳng đến đường thẳng đó, đường xiên lớn hơn sẽ có hình chiếu nhỏ hơn.
D. Nếu hai đường xiên từ một điểm ngoài một đường thẳng đến đường thẳng đó bằng nhau, thì hai hình chiếu của chúng cũng bằng nhau; ngược lại, nếu hai hình chiếu bằng nhau, thì hai đường xiên cũng bằng nhau.
Câu 2: Cho đường thẳng d và điểm A không nằm trên đường thẳng d. Chọn phát biểu sai.
A. Từ điểm A có thể kẻ duy nhất một đường vuông góc đến đường thẳng d.
B. Từ điểm A đến đường thẳng d có vô số đường xiên có thể kẻ.
C. Từ điểm A đến đường thẳng d có thể kẻ vô số đường vuông góc.
D. Trong số các đường xiên và đường vuông góc từ điểm A đến đường thẳng d, đường vuông góc luôn là đoạn ngắn nhất.
Câu 3: Xét tam giác ABC với D và E lần lượt là hình chiếu của B và C lên AC và AB. Khi đó có:
A. BD + CE lớn hơn AB cộng AC.
B. BD + CE nhỏ hơn tổng AB và AC.
C. BD + CE bằng tổng AB và AC.
D. BD + CE bằng một nửa tổng AB và AC.
Câu 4: Trong tam giác ABC vuông tại A, từ A hạ một đường vuông góc AH đến BC tại điểm H. Khi đó có:
A. Đoạn AH dài hơn đoạn BC.
B. Đoạn AH bằng đoạn BC.
C. Đoạn AH ngắn hơn đoạn BC.
D. Đoạn AH dài gấp đôi đoạn BC.
Câu 5: Trong tam giác ABC nhọn, vẽ tia Ax nằm trong góc BAC và cắt BC tại M. E và F lần lượt là hình chiếu của B và C lên tia Ax. So sánh tổng BE và CF với đoạn BC.
A. Tổng BE và CF nhỏ hơn đoạn BC.
B. Tổng BE và CF lớn hơn đoạn BC.
C. Tổng BE và CF bằng đoạn BC.
D. Tổng BE và CF gấp đôi đoạn BC.
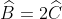
A. Đoạn BD bằng đoạn DC.
B. Đoạn AE bằng đoạn EB.
C. Đoạn EB bằng đoạn ED.
D. Trong tam giác vuông ΔABC tại B, đoạn DA bằng đoạn DC và đoạn DB.
Câu 7: Xét tam giác vuông ΔABC tại A, với M là trung điểm của AC. D và E lần lượt là hình chiếu của A và C lên đường thẳng BM. So sánh tổng BD và BE với đoạn AB.
A. Tổng BD và BE lớn hơn gấp đôi đoạn AB.
B. Tổng BD và BE nhỏ hơn gấp đôi đoạn AB.
C. Tổng BD và BE bằng gấp đôi đoạn AB.
D. Tổng BD và BE nhỏ hơn đoạn AB.
Câu 8: Xem hình vẽ sau:
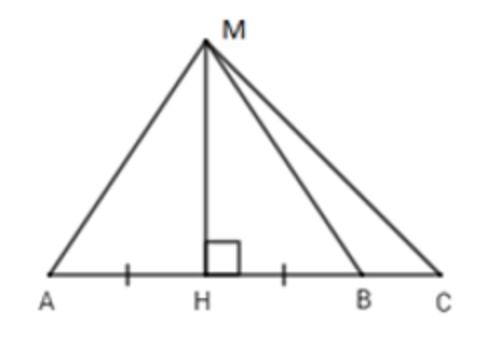
Chọn phát biểu sai trong số các phát biểu dưới đây:
A. Đoạn MA dài hơn đoạn MH.
B. Đoạn HB ngắn hơn đoạn HC.
C. Đoạn MA bằng đoạn MB.
D. Đoạn MC ngắn hơn đoạn MA.
Câu 9: Trong tam giác ABC với chiều cao AH:
A. Nếu BH nhỏ hơn HC thì AB nhỏ hơn AC.
B. Nếu AB nhỏ hơn AC thì BH nhỏ hơn HC.
C. Nếu BH bằng HC thì AB bằng AC.
D. Các phát biểu A, B, C đều đúng.
Câu 10: Xét ba điểm A, B, C trên một đường thẳng, với B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B, chọn điểm H. Khi đó:
A. Đoạn AH ngắn hơn đoạn BH.
B. Đoạn AH ngắn hơn đoạn AB.
C. Đoạn AH dài hơn đoạn BH.
D. Đoạn AH bằng đoạn BH.
Câu 16: Trong tam giác ABC, với AB lớn hơn AC. D là trung điểm của cạnh BC. So sánh chiều dài của đoạn AD với đoạn BD.
A. Đoạn AD ngắn hơn đoạn BD.
B. Đoạn AD dài hơn đoạn BD.
C. Đoạn AD bằng đoạn BD.
D. Không thể xác định được mối quan hệ.
Câu 17: Trong tam giác vuông ABC tại A, với AB dài 8 cm và AC dài 15 cm. Tìm chiều dài của đoạn BC.
A. 10 cm
B. 13 cm
C. 17 cm
D. 20 cm
Câu 18: Trong tam giác ABC, góc A nhỏ hơn cả góc B và góc C. So sánh chiều dài của đoạn AB với đoạn BC.
A. Đoạn AB ngắn hơn đoạn BC.
B. Đoạn AB dài hơn đoạn BC.
C. Đoạn AB bằng đoạn BC.
D. Không thể xác định được mối quan hệ.
Câu 19: Trong tam giác ABC, với các cạnh AB và AC có độ dài lần lượt là 5 cm và 6 cm, hãy so sánh độ dài của đoạn AH và BH khi H là trực tâm từ đỉnh A.
A. AH nhỏ hơn BH
B. AH lớn hơn BH
C. AH bằng BH
D. Không thể xác định được mối quan hệ giữa AH và BH
Câu 20: Trong tam giác vuông ABC tại đỉnh A, với cạnh huyền BC dài 10 cm, hãy tính độ dài của đoạn BD, trong đó D là trung điểm của cạnh AC.
A. 5 cm
B. 7.5 cm
C. 10 cm
D. 12.5 cm
KẾT QUẢ CHI TIẾT:
Câu 1: Trong các phát biểu, phát biểu C là không chính xác và là lựa chọn đúng.
Giải thích: Trong hai đường xiên từ một điểm ngoài một đường thẳng đến đường thẳng đó, đường xiên dài hơn sẽ có hình chiếu dài hơn.
Câu 2: Lựa chọn chính xác là C
Giải thích: Chúng ta biết rằng chỉ có một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước, còn có vô số đường thẳng đi qua một điểm cho trước và cắt một đường thẳng cho trước. Vì vậy, đường vuông góc từ điểm A đến đường thẳng d là duy nhất, còn đường xiên từ A đến d là vô số. Do đó, A và B đúng, C sai, và đáp án D đúng theo lý thuyết đã cho.
Câu 3: Lựa chọn chính xác là B
Giải thích:
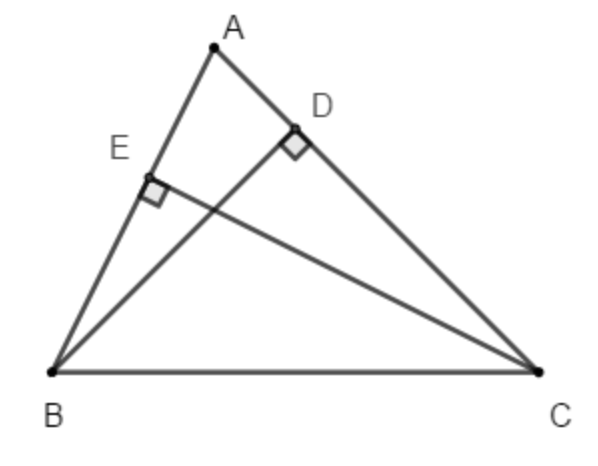
D là hình chiếu của B trên AC
⇒ BD nhỏ hơn BA (theo mối quan hệ giữa đường vuông góc và đường xiên)
E là hình chiếu của C trên AB
⇒ CE nhỏ hơn AC (theo mối quan hệ giữa đường vuông góc và đường xiên)
Từ đó ta có: BD + CE nhỏ hơn BA + AC = AB + AC
Vậy BD + CE nhỏ hơn AB + AC
Câu 4: Lựa chọn chính xác là C
Giải thích:
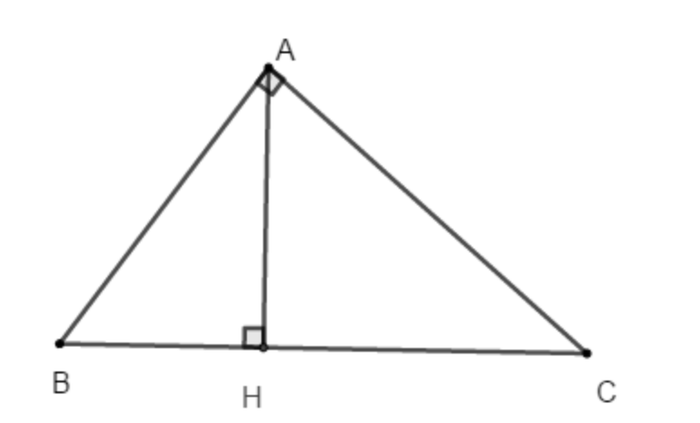
Tam giác vuông tại đỉnh A với cạnh huyền là BC
⇒ AC nhỏ hơn BC
Tam giác AHC vuông tại H với AC là cạnh huyền
⇒ AH nhỏ hơn AC
Do đó, ta có: AH nhỏ hơn AC nhỏ hơn BC
Vì vậy, AH nhỏ hơn BC
Câu 5: Lựa chọn chính xác là A
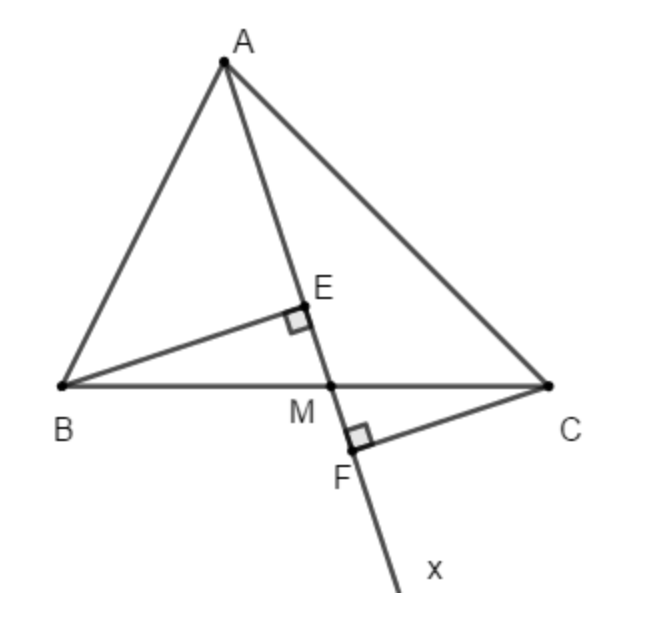
Do BE vuông góc với Ax tại điểm E, nên tam giác BEM vuông tại E
⇒ BM lớn hơn BE (theo mối quan hệ giữa đường xiên và đường vuông góc)
Vì CF vuông góc với Ax tại điểm F, nên tam giác CFM vuông tại F
⇒ CM lớn hơn CF (theo mối quan hệ giữa đường xiên và đường vuông góc)
Do đó, ta có: BM + CM lớn hơn BE + CF
vì BM + CM = BC (với M nằm trên BC)
Vì vậy: BC lớn hơn BE + CF hay BE + CF nhỏ hơn BC
Câu 6: Lựa chọn chính xác là B
Giải thích:
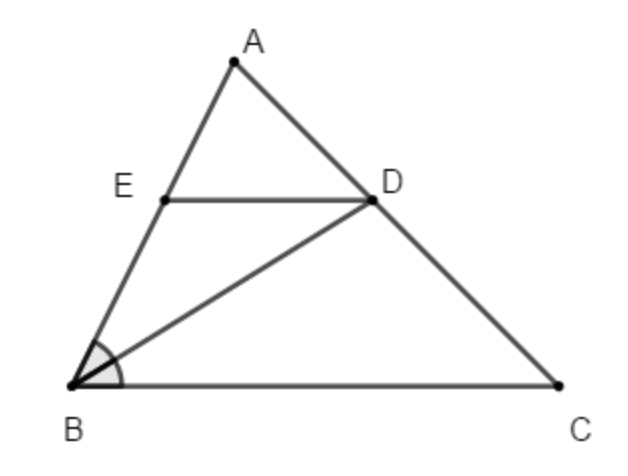
Câu 7: Lựa chọn chính xác là A
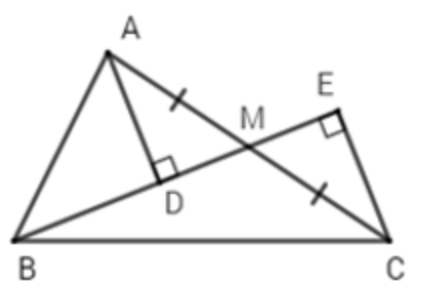
Giải thích:
Trong tam giác ΔABM vuông tại A (theo giả thiết), ta có BA nhỏ hơn BM (theo mối quan hệ giữa đường vuông góc và đường xiên)
Vì BM = BD + DM, nên BA nhỏ hơn BD + DM (1)
Ngoài ra: BM = BE - ME, nên BA nhỏ hơn BE - ME (2)
Cộng hai vế của (1) và (2) ta có: 2BA nhỏ hơn BD + BE + MD - ME (3)
Vì M là trung điểm của AC (theo giả thiết), ta có AM bằng MC (theo tính chất trung điểm)
Xem xét tam giác vuông ADM và tam giác vuông CEM với AM = MC (theo nhận xét)
∠AMD = ∠EMC (do đối đỉnh)
Do đó: ΔADM bằng ΔCEM (cạnh huyền – góc nhọn)
⇒ MD bằng ME (4) (hai cạnh tương ứng), từ (3) và (4) suy ra BD + BE lớn hơn 2AB
Câu 8: Lựa chọn chính xác là D
Giải thích:
Vì MH là đường vuông góc và MA là đường xiên nên MA lớn hơn MH (theo mối quan hệ giữa đường vuông góc và đường xiên), do đó A là đúng.
Do ∠MBC là góc ngoài của ΔMHB nên ∠MBC lớn hơn ∠MHB = 90°
Xem xét ΔMBC với ∠MBC là góc tù, từ đó suy ra MC lớn hơn MB (theo mối quan hệ giữa góc và cạnh trong tam giác)
HB và HC lần lượt là hình chiếu của MB và MC trên AC.
⇒ HB nhỏ hơn HC (theo mối quan hệ giữa đường xiên và hình chiếu), do đó B là đúng.
Vì AH = HB (theo giả thiết) và AH, HB lần lượt là hình chiếu của AM và BM.
⇒ MA = MB (theo mối quan hệ giữa đường xiên và hình chiếu), do đó C là đúng.
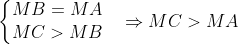
Câu 9: Lựa chọn chính xác là D
Giải thích:
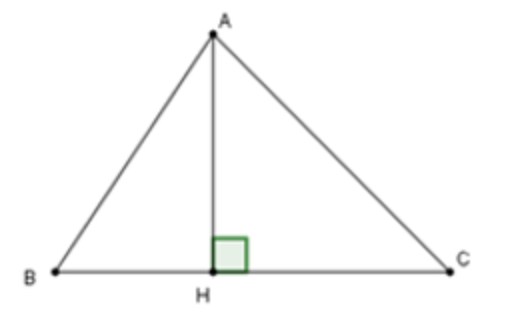
Trong tam giác ABC, AH là đường vuông góc, còn BH và CH là hình chiếu của các đường xiên AB và AC lên AH.
Theo mối quan hệ giữa đường xiên và hình chiếu, ta có các trường hợp sau:
- Nếu BH nhỏ hơn HC, thì AB nhỏ hơn AC
- Nếu AB nhỏ hơn AC, thì BH nhỏ hơn HC
- Nếu BH bằng HC, thì AB bằng AC
Vậy tất cả các lựa chọn A, B, C đều đúng.
Câu 10: Lựa chọn chính xác là C
Giải thích:
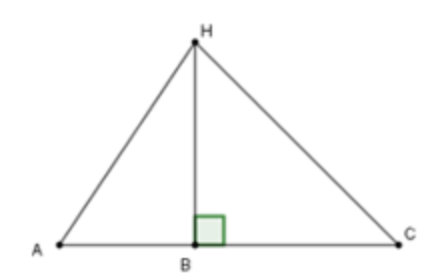
Vì BH là đường vuông góc và AH là đường xiên nên AH lớn hơn BH
