1. Tổng quan về đoạn thẳng và cách xác định độ dài đoạn thẳng
Đoạn thẳng là phần của đường thẳng được giới hạn bởi hai điểm cụ thể, có độ dài hữu hạn và không bị gấp khúc. Hai điểm này, gọi là điểm đầu và điểm cuối, là các điểm xác định của đoạn thẳng.
Ví dụ minh họa đoạn thẳng với hai điểm AB
- Đặc điểm của đoạn thẳng: Đoạn thẳng là một phần của đường thẳng có độ dài xác định và không bị cong hay gập khúc. Tất cả các điểm trên đoạn thẳng đều nằm thẳng hàng.
- Điểm đầu và điểm cuối: Đoạn thẳng được xác định bởi hai điểm, điểm đầu là điểm bắt đầu và điểm cuối là điểm kết thúc của đoạn thẳng.
- So sánh đoạn thẳng và đường thẳng: Đoạn thẳng là phần hữu hạn của đường thẳng, trong khi đường thẳng kéo dài vô hạn theo cả hai hướng. Đoạn thẳng chỉ bao gồm các điểm nằm giữa hai điểm đầu và cuối.
- Tính chất của đoạn thẳng: Đoạn thẳng có thể di chuyển và xoay mà không thay đổi độ dài. Tuy nhiên, nếu kéo dài hoặc co lại, nó sẽ không còn giữ hình dạng đoạn thẳng nữa.
- Đoạn thẳng luôn có một độ dài cụ thể, và khi chọn một đơn vị đo, độ dài của đoạn thẳng được biểu thị bằng một số dương kèm theo đơn vị tương ứng.
- Độ dài của đoạn thẳng AB, hay còn gọi là khoảng cách giữa hai điểm A và B, được quy ước là 0 khi hai điểm trùng nhau.
- Đơn vị đo độ dài của đoạn thẳng có thể là mm (milimet), cm (centimet), dm (decimet), m (mét), inch (in), foot (ft), và nhiều đơn vị khác.
- Ứng dụng của đoạn thẳng rất đa dạng: trong đồ họa máy tính, đoạn thẳng giúp vẽ hình dạng và kết nối các điểm; trong vật lý, nó hỗ trợ trong việc mô phỏng và tính toán quỹ đạo cũng như vị trí của các vật thể.
- Tóm lại, đoạn thẳng là phần hữu hạn của đường thẳng, có hai điểm đầu cuối và độ dài xác định. Đây là khái niệm cơ bản trong toán học với nhiều ứng dụng thực tiễn.
2. Giải Toán 6 Bài 34: Khám phá đoạn thẳng và cách đo độ dài đoạn thẳng
Câu 1: Hãy liệt kê các đoạn thẳng có mặt trong hình vẽ dưới đây.
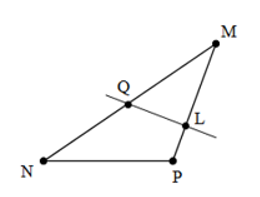
A. MN; MQ; NQ; ML; LP; MP; NP; QL
B. MN; QL; MQ; NQ; ML; LP; MP
C. MN; MQ; NQ; ML; QL; MP; NP
D. MN; MQ; ML; MP; NP
Đáp án chính xác: Các đoạn thẳng có trong hình vẽ là MN; MQ; NQ; ML; LP; MP; NP; QL, vì vậy đáp án đúng là: A.
Câu 2: Xét điểm G nằm trên đoạn thẳng HK (G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm ở giữa hai điểm còn lại?
A. Điểm G
B. Điểm H
C. Điểm K
D. Không có điểm nào nằm giữa hai điểm còn lại.
Giải thích chi tiết: Vì G nằm trên đoạn thẳng HK, nên G ở giữa hai điểm H và K. Do đó, đáp án chính xác là: A.
Câu 3. Nếu điểm P nằm giữa hai điểm M và N, thì:
A. PN + MN = PN
B. MP + MN = PN
C. MP + PN = MN
D. MP – PN = MN
Giải thích chi tiết: Khi điểm P nằm giữa M và N, ta có MP + PN = MN. Do đó, đáp án đúng là: C.
Câu 4. Khi một đoạn thẳng cắt qua một tia, số điểm chung giữa đoạn thẳng và tia là bao nhiêu?
A. 1
B. 2
C. 0
D. Vô số
Giải thích chi tiết: Khi một đoạn thẳng cắt một tia, chúng có duy nhất một điểm giao nhau. Do đó, lựa chọn đúng là: A.
Câu 5: Với 10 điểm phân biệt trong đó không có ba điểm nào nằm trên một đường thẳng, mỗi cặp điểm sẽ xác định một đoạn thẳng. Hãy tính tổng số đoạn thẳng có thể vẽ được.
A. 10
B. 90
C. 40
D. 45
Giải thích chi tiết: Tổng số đoạn thẳng cần tìm là 45. Do đó, đáp án chính xác là: D.
Câu 7. Đường thẳng xx′ sẽ cắt qua bao nhiêu đoạn thẳng trong hình vẽ dưới đây?

A. 3
B. 4
C. 5
D. 6
Giải thích chi tiết: Đường thẳng xx′ cắt qua năm đoạn thẳng: OA, OB, AB, MA và MB. Do đó, đáp án đúng là: C.
Câu 8. Xét các đoạn thẳng AB = 4cm, MN = 5cm, EF = 3cm, PQ = 4cm, IK = 5cm. Chọn đáp án không chính xác.
A. AB nhỏ hơn MN
B. EF nhỏ hơn IK
C. AB bằng PQ
D. AB bằng EF
Giải thích chi tiết:
- Đáp án A: AB nhỏ hơn MN là chính xác vì AB = 4cm nhỏ hơn MN = 5cm.
- Đáp án B: EF nhỏ hơn IK là đúng vì EF = 3cm nhỏ hơn IK = 5cm.
- Đáp án C: AB bằng PQ là đúng vì cả hai đoạn đều dài 4cm.
- Đáp án D: AB bằng EF là sai vì AB = 4cm lớn hơn EF = 3cm.
Do đó, đáp án chính xác là đáp án D.
3. Bài tập ứng dụng trong Toán lớp 6 về đường thẳng và độ dài đoạn thẳng
Bài 1: Sử dụng compa để vẽ một đường tròn với tâm O và bán kính 2 cm. Chọn hai điểm M và N tùy ý trên đường tròn. Liệu hai đoạn thẳng OM và ON có bằng nhau không?
- Phương pháp giải: Đặt điểm O trên giấy và mở compa sao cho bán kính bằng 2 cm. Đặt đầu nhọn của compa tại O rồi vẽ đường tròn theo kích thước đã chọn.
- Giải: Vì M và N đều nằm trên đường tròn với tâm O và mọi điểm trên đường tròn đều cách tâm một khoảng bằng bán kính R, nên OM và ON đều bằng bán kính của đường tròn.
Bài 2: Bạn Tuấn dùng thước đo độ dài của đoạn CD, nhưng vì thước bị gãy nên chỉ có thể đặt điểm C trùng với vạch 2 cm và điểm D trùng với vạch 10 cm. Tính độ dài của đoạn thẳng CD.
- Phương pháp giải: Đo thực tế đoạn thẳng CD, sau đó trừ đi phần thước bị gãy để tính ra độ dài chính xác của đoạn thẳng CD.
- Giải: Kết quả đo điểm D là 10 cm, trừ đi điểm C với vạch 2 cm.
Vậy, độ dài đoạn thẳng CD là: 10 cm - 2 cm = 8 cm.
Do đó, đáp án là: Đoạn thẳng CD dài 8 cm.
Bài 3: Bạn Tuấn sử dụng bước chân để đo chiều dài lớp học. Sau 10 bước liên tiếp từ mép tường đầu lớp, còn khoảng nửa bước chân nữa là tới mép tường cuối lớp. Nếu mỗi bước chân dài khoảng 0,7 m, thì lớp học dài khoảng bao nhiêu?
- Phương pháp giải: Tính tổng chiều dài của 10 bước chân cộng với chiều dài của nửa bước chân.
Nếu mỗi bước dài 0,6 m thì nửa bước có chiều dài là 0,5 x 0,6 m.
- Giải: Tổng chiều dài lớp học là: 0,6 m x 10 bước + (0,6 m x 0,5 bước) = 7,2 m.
Do đó, lớp học dài khoảng 7,2 m.
Bài 4: Một cái cây thẳng đứng bị bão làm gãy phần ngọn. Đo được phần ngọn bị gãy dài 2 m và phần thân còn lại dài 1,5 m. Vậy cây cao bao nhiêu mét trước khi bị gãy?
- Phương pháp giải: Để tính chiều cao của cây, ta cộng chiều dài phần ngọn với phần thân.
- Giải: Chiều cao của cây trước khi bị gãy là: 2 m + 1,5 m = 3,5 m.
Do đó, cây cao 3,5 m trước khi bị gãy.
Chúng tôi xin kết thúc bài tư vấn tại đây, cảm ơn quý vị đã theo dõi!
