Giải Toán 9 Bài 2: Hướng Dẫn Chi Tiết Về Hàm Số Bậc Nhất

Buzz

Nội dung bài viết

A. Kiến Thức Cơ Bản Về Hàm Số Bậc Nhất

1. Khái Niệm

2. Đặc Điểm

3. Đặc Điểm Của Đồ Thị Hàm Số y = ax + b (a ≠ 0)

B. Hướng Dẫn Giải Bài Tập Trang 48 SGK Toán 9 Tập 1

C. Giải Toán 9 Trang 48 Tập 1: Bài Tập Luyện Tập

D. Bài tập ứng dụng liên quan

Xem thêm

Mytour xin gửi đến bạn đọc hướng dẫn giải chi tiết các bài tập trong sách giáo khoa Toán 9 tập 1, Chương 2: Hàm Số Bậc Nhất. Hãy xem từng bài để nắm bắt lời giải cụ thể.

A. Kiến Thức Cơ Bản Về Hàm Số Bậc Nhất

1. Khái Niệm

- Hàm số bậc nhất là một hàm số có dạng y = ax + b, với a và b là các số thực cho trước, và a không bằng 0.

- Đặc biệt, khi b = 0, hàm số bậc nhất trở thành hàm số y = ax, thể hiện mối liên hệ tỉ lệ thuận giữa y và x

2. Đặc Điểm

a) Hàm số bậc nhất y = ax + b có giá trị xác định cho mọi x thuộc R

b) Trong tập số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

Hàm số y = f(x) được gọi là đồng biến trong một khoảng nếu với mọi x1 và x2 trong khoảng đó, khi x1 < x2 thì f(x1) < f(x2)

Hàm số y = f(x) được gọi là nghịch biến trong một khoảng nếu với mọi x1 và x2 trong khoảng đó, khi x1 < x2 thì f(x1) > f(x2)

3. Đặc Điểm Của Đồ Thị Hàm Số y = ax + b (a ≠ 0)

a) Đồ thị của hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ, được gọi là đường thẳng y = ax. Nếu a > 0, đường thẳng y = ax nằm trong góc phần tư thứ I và III; nếu a < 0, nó nằm trong góc phần tư thứ II và IV

b) Đồ thị hàm số y = ax + b là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và song song với đường thẳng y = ax nếu b ≠ 0; nếu b = 0, nó trùng với đường thẳng y = ax.

Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) cũng gọi là đường thẳng y = ax + b, trong đó b là tung độ gốc của đường thẳng.

B. Hướng Dẫn Giải Bài Tập Trang 48 SGK Toán 9 Tập 1

Giải Toán 9 Bài 8 Trang 48 SGK Tập 1

Trong số các hàm số dưới đây, hãy xác định hàm số nào là hàm số bậc nhất. Tìm các hệ số a, b của chúng và phân tích xem hàm số bậc nhất nào đồng biến hoặc nghịch biến.

a) y = 1 - 5x;

b) y = -0,5x;

$\sqrt{2}\left(x+1\right)+\sqrt{3}$ $2x^{2}$

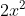
Giải:

a) y = 1 - 5x là hàm số bậc nhất với a = -5 và b = 1. Hàm số này là nghịch biến vì hệ số a < 0.

b) y = -0,5x là hàm số bậc nhất với a ≈ -0,5 và b = 0. Hàm số này là nghịch biến do a < 0.

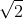
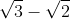
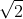
$\sqrt{2}\left(x+1\right)+\sqrt{3}$ $\sqrt{2}$ $\sqrt{3} - \sqrt{2}$ $\sqrt{2}$ $2x^{2}$

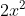
Giải Bài Tập Toán 9 Bài 9 Trang 48 SGK Tập 1

Xét hàm số bậc nhất y = (m - 2)x + 3. Xác định các giá trị của m để hàm số:

a) Đồng biến;

b) Nghịch biến.

Giải:

a) Hàm số: y = (m−2)x + 3 đồng biến trên R khi:

⇔ m − 2 > 0 ⇔ m > 2

b) Hàm số: y = (m − 2)x + 3 nghịch biến trên R khi:

⇔ m − 2 < 0 ⇔ m < 2

Giải Bài Tập Toán 9 Bài 10 Trang 48 SGK Tập 1

Một hình chữ nhật có kích thước 20 cm và 30 cm. Nếu giảm mỗi kích thước đi x (cm), ta sẽ có một hình chữ nhật mới với chu vi là y (cm). Xác định công thức tính y theo x.

Giải:

Khi giảm mỗi kích thước x (cm), ta có được hình chữ nhật với kích thước là 20 - x (cm) và 30 - x (cm).

Vì vậy, chu vi của hình chữ nhật mới là y = 2(20 − x + 30 − x) hay y = 100 − 4x

C. Giải Toán 9 Trang 48 Tập 1: Bài Tập Luyện Tập

Giải bài tập Toán lớp 9, bài 11, trang 48 sách giáo khoa tập 1

Biểu diễn các điểm sau trên mặt phẳng tọa độ:

A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), F(1; -1), G(0; -3), H(-1; -1).

Giải:

Mặt phẳng tọa độ thể hiện các điểm như sau:

Giải bài tập Toán lớp 9, bài 12, trang 48 sách giáo khoa tập 1

Xét hàm số bậc nhất y = ax + 3. Tìm hệ số a khi biết rằng khi x = 1 thì y = 2,5.

Giải:

Dựa vào đề bài, ta có:

Hàm số y = ax + 3 đi qua điểm A(1; 2,5)

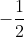
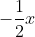
$-\frac{1}{2}$ $-\frac{1}{2}x + 3$

Giải bài tập Toán lớp 9, bài 13, trang 48 sách giáo khoa tập 1

Dưới những điều kiện nào của m thì các hàm số sau đây là hàm số bậc nhất?

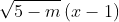
$\sqrt{5-m}\left(x-1\right)$ $\frac{m+1}{m-1}x$

Giải:

Để một hàm số trở thành hàm số bậc nhất, nó cần có dạng y = ax + b với a khác 0. Vì vậy:

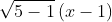
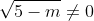
$\sqrt{5-1}\left(x-1\right)$ $\sqrt{5-m}\ne0$ $\frac{m+1}{m-1}x$ $\frac{m+1}{m-1}\ne0$

Giải bài tập Toán lớp 9, bài 14, trang 48 sách giáo khoa tập 1

Hàm số bậc nhất có dạng y = (1 - √5)x – 1.

a) Hàm số trên là đồng biến hay nghịch biến trên tập R? Giải thích lý do.

b) Tính giá trị của y khi x = 1 + √5.

c) Tính giá trị của x khi y = √5.

Gợi ý đáp án

a) Ta có:

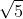
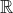
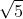
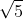
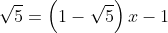
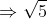
$\sqrt{5}$ $\mathbb{R}$ $\sqrt{5}$ $\left(1 - \sqrt{5}\right)\left(1 + \sqrt{5}\right)$ $\left(1 - 5\right)$ $\sqrt{5}$ $\sqrt{5} = \left(1 - \sqrt{5}\right)x - 1$ $\Rightarrow \sqrt{5} + 1 = \left(1 - \sqrt{5}\right)x$ $\Rightarrow x = \frac{1 + \sqrt{5}}{1 - \sqrt{5}} = \frac{\left(1 + \sqrt{5}\right)^2}{\left(1 - \sqrt{5}\right)^2} = \frac{1 + 2\sqrt{5} + 5}{1 - 2\sqrt{5} + 5} = \frac{6 + 2\sqrt{5}}{6 - 2\sqrt{5}} = \frac{1 + \sqrt{5}}{-4}$

D. Bài tập ứng dụng liên quan

Bài tập số 1: Một hình vuông có cạnh dài 15 cm. Nếu giảm mỗi cạnh đi x cm, hãy viết công thức tính diện tích của hình vuông mới theo x.

Lời giải chi tiết:

Diện tích của hình vuông ban đầu là cạnh x cạnh = 15 x 15 = 225 cm²

Sau khi giảm x cm từ mỗi cạnh, cạnh của hình vuông mới sẽ là 15 - x cm

$(15 - x)^{2}$

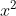
Do đó, công thức tính diện tích của hình vuông mới sau khi giảm x cm từ mỗi cạnh là: 225 - 30x + x^{2} (cm²)

Bài tập số 2: Một hình tam giác đều có cạnh dài 18 cm. Nếu giảm mỗi cạnh đi x cm, hãy viết công thức tính chu vi của tam giác mới theo x.

Lời giải chi tiết:

Chu vi của hình tam giác đều ban đầu là: số cạnh x độ dài mỗi cạnh = 3 x 18 = 54 cm

Sau khi giảm x cm từ mỗi cạnh, độ dài của mỗi cạnh mới sẽ là 18 - x (cm)

Chu vi của hình tam giác mới được tính bằng công thức: số cạnh nhân với độ dài cạnh mới = 3 x (18 - x) = 54 - 3x (cm)

Do đó, công thức để tính chu vi của hình tam giác mới, sau khi giảm mỗi cạnh đi x cm, là: y = 54 - 3x (cm)

Bài tập số 3: Một hình ngũ giác đều với mỗi cạnh dài 25 cm. Nếu giảm mỗi cạnh đi x cm, hãy xác định công thức tính chu vi của ngũ giác mới theo x.

Giải chi tiết:

Chu vi của hình ngũ giác đều ban đầu là số cạnh nhân với độ dài cạnh = 5 x 25 = 125 (cm)

Khi giảm mỗi cạnh đi x cm, chiều dài cạnh mới sẽ trở thành 25 - x (cm)

Do đó, công thức tính chu vi của ngũ giác mới, sau khi giảm mỗi cạnh đi x cm, là: y = 125 - 5x (cm)

Bài tập số 4: Một hình bát giác đều với mỗi cạnh dài 12 cm. Nếu giảm mỗi cạnh đi x cm, hãy xác định công thức tính chu vi của bát giác mới theo x.

Giải chi tiết:

Chu vi của hình bát giác đều ban đầu là số cạnh nhân với độ dài mỗi cạnh = 8 x 12 = 96 (cm)

Khi giảm mỗi cạnh đi x cm, độ dài của mỗi cạnh mới sẽ còn lại 12 - x (cm)

Chu vi của bát giác mới được tính bằng số cạnh nhân với độ dài cạnh mới, tức là 8 x (12 - x) = 96 - 8x (cm)

Do đó, công thức tính chu vi của bát giác mới sau khi giảm mỗi cạnh đi x cm là y = 96 - 8x (cm).

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]