A. Lý thuyết về quy tắc dấu ngoặc
1. Quy tắc về dấu ngoặc
Khi loại bỏ dấu ngoặc với dấu '-' đứng trước, ta cần đổi dấu tất cả các số hạng bên trong ngoặc: dấu '-' thành dấu '+' và dấu '+' thành dấu '-'. Ngược lại, nếu dấu ngoặc có dấu '+' đứng trước, các dấu của các số hạng trong ngoặc không thay đổi.
2. Tổng đại số
Phép trừ một số tương đương với phép cộng số đối của nó, do đó một chuỗi các phép cộng và trừ có thể được chuyển đổi thành một chuỗi các phép cộng thuần túy. Vì vậy, một chuỗi các phép toán cộng và trừ các số nguyên được gọi là tổng đại số.
Khi viết tổng đại số, để đơn giản hóa, sau khi chuyển các phép trừ thành phép cộng (với số đối tương ứng), bạn có thể bỏ qua tất cả các dấu cộng và dấu ngoặc.
Lưu ý: Trong một tổng đại số, bạn có thể:
+ Tự do thay đổi vị trí của các số hạng cùng với dấu của chúng.
+ Bạn có thể tự do đặt dấu ngoặc để nhóm các số hạng, lưu ý rằng nếu dấu ngoặc đứng sau dấu '-', tất cả các số hạng trong ngoặc phải đổi dấu.
B. Giải Toán lớp 6 bài 15: Quy tắc dấu ngoặc theo chương trình Kết nối tri thức
Chi tiết hướng dẫn giải các bài tập trong sách giáo khoa Toán 6 Kết nối tri thức về Quy tắc dấu ngoặc có tại:
* Toán lớp 6 bài 15: Quy tắc dấu ngoặc - Kết nối tri thức
C. Giải bài tập trong sách giáo khoa Toán lớp 6 tập 1 - Sách Cũ
Câu hỏi 1 trang 83 sách giáo khoa Toán lớp 6 tập 1
a) Xác định số đối của các số: 2, (-5), và tổng của 2 + (-5)
b) So sánh số đối của tổng 2 + (-5) với tổng các số đối của 2 và (-5)
Hướng dẫn giải chi tiết
a) Số đối của 2 là: -2
Số đối của -5 là 5
Vì 2 cộng với (-5) bằng -3, nên số đối của -3 là 3
b) Kết quả là 2 + (-5) = 2 + (-5)
Câu hỏi 2 trang 83 sách giáo khoa Toán lớp 6 tập 1
Tính toán và so sánh kết quả của các phép toán sau đây:
a) 7 + (5 - 13) và 7 + 5 - 13
b) 12 - (4 - 6) và 12 - 4 + 6
Hướng dẫn giải chi tiết
a) 7 + (5 - 13) = 7 - 8 = -1
7 + 5 - 13 = 12 - 13 = -1
Do đó, 7 + (5 - 13) bằng 7 + 5 - 13
b) 12 - (4 - 6) bằng 12 - (-2) = 12 + 2 = 14
12 - 4 + 6 = 8 + 6 = 14
Vì vậy, 12 - (4 - 6) cũng chính là 12 - 4 + 6
Câu hỏi 3 trang 83 SGK Toán 6 tập 1
Tính nhanh các bài toán sau:
a) (768 - 39) - 768 b) (-1579) - (12 - 1579)
Hướng dẫn giải chi tiết:
a) (768 - 39) - 768 = 768 - 39 - 768 = (768 - 768) - 39 = 0 - 39 = -39
b) (-1579) - (12 - 1579) = -1579 - 12 + 1579 = (-1579 + 1579) - 12 = 0 - 12 = -12
Bài 57 trang 85 SGK Toán 6 tập 1
Tính tổng các biểu thức sau:
a) (-17) + 5 + 8 + 17; b) 30 + 12 + (-20) + (-12);
c) (-4) + (-440) + (-6) + 440; d) (-5) + (-10) + 16 + (-1).
Hướng dẫn cách giải:
+ Khi loại bỏ dấu ngoặc với dấu '-' trước, chúng ta cần đổi dấu tất cả các số hạng trong ngoặc: đổi dấu '-' thành dấu '+' và ngược lại. Với dấu '+' trước ngoặc, các dấu trong ngoặc không thay đổi.
+ Hai số đối nhau là hai số có tổng bằng 0.
Hướng dẫn chi tiết cách giải
a) (-17) + 5 + 8 + 17
= [(-17) + 17] + (5 + 8)
= 0 + 13 = 13
b) 30 + 12 + (-20) + (-12)
= [30 + (-20)] + [12 + (-12)]
= 10 + 0 = 10
c) (-4) + (-440) + (-6) + 440
= [(-4) + (-6)] + [(-440) + 440]
= (-10) + 0 = -10
d) (-5) + (-10) + 16 + (-1)
= [(-5) + (-10) + (-1)] + 16
= (-16) + 16 = 0
Bài 58 trang 85 SGK Toán 6 tập 1
Rút gọn biểu thức:
a) x + 22 + (-14) + 52 b) (-90) – (p + 10) + 100.
Hướng dẫn:
+ Khi loại bỏ dấu ngoặc với dấu '-' trước, cần đổi dấu tất cả các số hạng bên trong: dấu '-' thành dấu '+' và ngược lại. Nếu dấu ngoặc có dấu '+' trước, các số hạng trong ngoặc vẫn giữ nguyên dấu.
Hướng dẫn chi tiết giải bài
a) x + (22 + 52) + (-14) = x + 74 - 14 = x + [74 - 14] = x + 60
b) (-90) - (p + 10) + 100 = (-90) - p - 10 + 100 = [(-90) - 10] - p + 100
= (-100) - p + 100 = 0 - p = -p
Bài 59 trang 85 SGK Toán 6 tập 1
Tính nhanh các tổng sau đây:
a) (2736 – 75) – 2736; b) (-2002) – (57 – 2002).
Hướng dẫn:
+ Khi loại bỏ dấu ngoặc với dấu '-' đứng trước, cần đổi dấu tất cả các số hạng bên trong: dấu '-' thành dấu '+' và ngược lại. Nếu có dấu '+' trước dấu ngoặc, các số hạng bên trong giữ nguyên dấu.
+ Hai số đối nhau có tổng bằng 0.
Hướng dẫn chi tiết cách giải
a) (2736 – 75) – 2736
= 2736 – 75 – 2736
= (2736 – 2736) – 75
= 0 – 75
= – 75
b) (-2002) – (57 – 2002)
= (-2002) – 57 + 2002
= (-2002 + 2002) – 57
= 0 – 57
= – 57
Bài 60 trang 85 SGK Toán 6 tập 1
Loại bỏ dấu ngoặc và tính toán:
a) (27 + 65) + (346 – 27 – 65) b) (42 – 69 + 17) – (42 + 17).
Hướng dẫn:
+ Khi loại bỏ dấu ngoặc với dấu '-' trước, ta cần thay đổi dấu của tất cả các số hạng trong ngoặc: dấu '-' thành dấu '+' và ngược lại. Nếu có dấu '+' trước ngoặc, các số hạng bên trong giữ nguyên dấu.
Hướng dẫn chi tiết cách giải
a) (27 + 65) + (346 - 27 - 65)
= 27 + 65 + 346 - 27 - 65
= (27 - 27) + (65 - 65) + 346
= 0 + 0 + 346 = 346
b) (42 - 69 + 17) - (42 + 17)
= 42 - 69 + 17 - 42 - 17
= (42 - 42) + (17 - 17) - 69
= 0 + 0 - 69 = -69
Bài tập luyện tập liên quan
a) (-385 + 210) + (385 - 217);
= -385 + 210 + 385 - 217 (bỏ dấu ngoặc tròn)
= (-385 + 385) - (217 - 210)
= 0 - 7
= -7
b) (72 - 1 956) - (-1 956 + 28).
= 72 - 1 956 + 1 956 - 28 (loại bỏ dấu ngoặc tròn)
= (1 956 - 1 956) + (72 - 28)
= 0 + 44
= 44
c) 12 + 13 + 14 - 15 - 16 - 17
= (12 - 15) + (13 - 16) + (14 - 17)
= (-3) + (-3) + (-3)
= - (3 + 3 + 3)
= -9
d) (35 - 17) - (25 - 7 + 22)
= 35 - 17 - 25 + 7 - 22
= (35 - 25) - (17 - 7) - 22
= 10 - 10 - 22
= 0 – 22
= - 22.
e) Cho bảng 3 x 3 như hình dưới. Hãy thay thế các ký tự trong bảng bằng các số sao cho tổng của các hàng, cột và đường chéo đều bằng 0
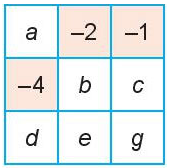
Đáp án:
Do a – 2 - 1 = 0 (theo (1)) nên a – 3 = 0 và a = 3
Vì tổng các số trong cột phải bằng 0 nên a + (-4) + d = 0 (4)
Thay a = 3 vào phương trình (4) ta có:
3 + (-4) + d = 0
3 – 4 + d = 0
-1 cộng d = 0
d = 0 + 1
d = 1
Do tổng các số trên đường chéo phải bằng 0 nên d + b + (-1) = 0 (5)
Thay d = 1 vào phương trình (5) ta có:
1 cộng b cộng (-1) = 0
b = 0
Vì tổng các số trong hàng ngang phải bằng 0 nên (-4) cộng b cộng c = 0 (6)
Thay b = 0 vào phương trình (6) ta có:
(-4) cộng 0 cộng c = 0
c – 4 = 0
c = 4
c = 4
Do tổng các số trên đường chéo phải bằng 0 nên a + b + g = 0 (7)
Thay a = 3 và b = 0 vào phương trình (7) ta có:
3 cộng 0 cộng g = 0
g cộng 3 = 0
g = -3
Vì tổng các số trong cột phải bằng 0 nên -2 cộng b cộng e = 0 (8)
Thay b = 0 vào phương trình (8) ta có:
-2 cộng 0 cộng e = 0
e – 2 = 0
e = 2
Vậy ta có a = 3; b = 0; c = 4; d = 1; e = 2; g = -3.
