A. Bắt đầu bài học
Xem xét các phương trình sau đây
a) 5y = 0
b) 2 − 3x = 0
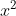
d) 5x + 1 = 0
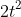
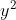
1. Xác định các phương trình bậc nhất trong số các phương trình trên và giải chúng
2. Đối với các phương trình không phải bậc nhất, hãy nhận xét về bậc của biến trong các phương trình đó và nêu phương pháp giải mà bạn biết.
Trả lời:
1. Các phương trình bậc nhất là: a, b, d
a) 5y = 0 ⇔ y = 0
b) 2 − 3x = 0 ⇔ 3x = 2 ⇔ x = 2/3
d) 5x + 1 = 0 ⇔ 5x = −1 ⇔ x = −1/5
2. Các phương trình không phải bậc nhất trong số các phương trình trên đều có bậc của biến là 2. Có thể giải các phương trình này bằng cách phân tích đa thức thành nhân tử.
B. Các hoạt động xây dựng kiến thức
1. a) Hoàn thiện các bước lập phương trình cho bài toán sau bằng cách điền vào chỗ trống (...)
Bài toán: Trên một mảnh đất hình chữ nhật có kích thước dài 32m và rộng 28m, bác Minh dự định xây dựng một khu vườn cây cảnh với lối đi xung quanh. Hãy tính bề rộng của lối đi sao cho diện tích khu đất còn lại là 672 m².
Xây dựng phương trình
Gọi bề rộng của lối đi là x (m), với điều kiện 0 < 2x < 28. Diện tích phần đất còn lại sẽ có hình dạng chữ nhật với các kích thước sau:
Chiều dài là: 32 − 2x (m)
Chiều rộng là: ...............
Diện tích còn lại là: (32 − 2x)(...................) (m²)
Dựa vào bài toán, ta có phương trình:
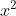
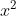
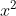
b) Đọc kỹ nội dung sau (sách giáo khoa trang 37)
c) Trong số các phương trình dưới đây, phương trình nào là phương trình bậc hai? Xác định các hệ số a, b, c của từng phương trình đó.
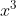
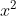
iii) −2x + 7 = 0
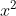
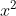
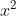
Trả lời:
a) Giả sử bề rộng của lối đi là x (m), với điều kiện 0 < 2x < 28. Kích thước phần đất còn lại sẽ là hình chữ nhật với:
Chiều dài là: 32 − 2x (m)
Chiều rộng là: 28 − 2x
Diện tích là: (32 − 2x) × (28 − 2x) (m²)
Dựa vào bài toán, ta có phương trình:
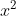
c) Các phương trình bậc hai gồm có:
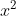
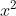
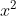
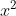
2. Hoàn thiện các bước vào chỗ trống (...) để
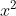
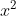
⇔x(............) = 0
⇔x = .............. hoặc ............. = 0
⇔x = hoặc x = ...........
Vậy ..............
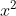
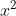
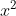
⇔ ..................
Vậy ....................
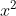
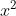
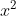
(Mâu thuẫn do .................)
Vậy .......................
Tham khảo: sách giáo khoa trang 38
Đáp án
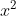
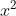
⇔x (3x − 2) = 0
⇔x = 0 hoặc 3x − 2 = 0
⇔x = 0 hoặc x = 2/3
Vậy các nghiệm của phương trình là: x = 0 hoặc x = 2/3
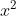
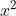
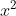
⇔x = ±√12
Vậy phương trình có hai nghiệm: x = ±√12
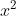
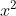
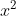
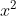
Vậy phương trình không có nghiệm.
3. Thực hiện các bước sau đây
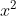
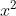
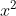
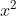
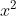
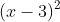
⇔ x − 3 = ................
⇔ x = 3 ± .................
Phương trình có hai nghiệm x₁ = ...............; x₂ = .....................
Tham khảo: sách giáo khoa trang 39
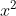
Đáp án:
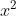
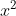
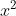
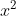
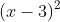
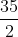
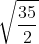
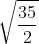
Phương trình có hai nghiệm.
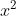
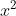
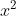
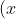
⇔ x + 2 = ±4
⇔ x = −2 ± 4
Vậy phương trình có hai nghiệm.
C. Bài tập và hướng dẫn giải
Câu 1: Trang 39 sách Toán VNNE lớp 9 tập 2
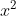
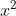
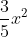

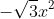
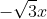
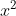
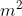
Lời giải chi tiết:
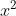
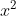
Các hệ số: a = 3; b = -7; c = 4
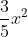

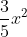
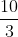

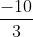
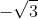
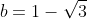
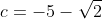
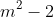
Giải bài 2 trang 39 sách toán VNEN lớp 9 tập 2
Giải các phương trình dưới đây:
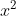
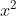
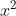
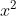
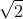
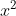
Giải chi tiết:
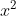
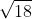
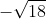
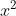
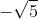
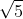
c, Phương trình không có nghiệm
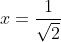
e, x = 0 hoặc x = 4
Giải bài 3 trang 39 sách toán VNEN lớp 9 tập 2
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình mà vế trái là một bình phương và vế phải là một hằng số.
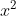
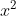
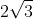
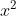
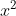
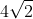
Giải chi tiết:

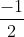
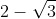


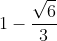
D, x = 1
D. Hoạt động ứng dụng và khám phá mở rộng
Câu 1: Trang 39 sách toán VNEN lớp 9 tập 2
Chuyển đổi vế trái của từng phương trình thành dạng tích rồi giải quyết:
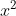
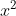
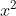
Giải chi tiết:
a, x = 1 hoặc x = -5
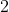
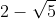

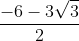
Giải bài 2 trang 39 sách toán VNEN lớp 9 tập 2
Giải những phương trình dưới đây:
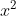
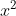
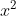
Chi tiết lời giải:
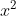
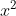
⇔ (x − 3) (x − 1) = 0
⇔ x = 3 hoặc x = 1
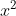
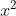
⇔ (x + 2) (2x + 1) = 0
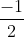
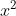
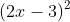
⇔ 2x − 3 = 0

Dưới đây là bài viết từ Mytour với hướng dẫn giải chi tiết nhất. Hy vọng thông tin trong bài viết sẽ giúp bạn đọc nắm vững kiến thức về hàm số bậc hai một ẩn và áp dụng để giải quyết bài tập hiệu quả. Mytour xin chân thành cảm ơn!
