1. Góc đồng vị là gì?
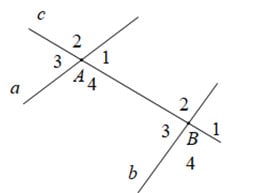
Khi một đường thẳng c cắt hai đường thẳng a và b tại các điểm A và B, nó tạo ra bốn cặp góc tại các đỉnh A và B. Các cặp góc A1 và B1, A2 và B2, A3 và B3, A4 và B4 được gọi là các góc đồng vị.
2. Đặc điểm của hai góc đồng vị:
Khi một đường thẳng c cắt hai đường thẳng a và b, và nếu trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì:
- Các góc so le trong còn lại cũng bằng nhau
- Các góc đồng vị là bằng nhau
.jpg)
Ví dụ: Theo hình minh họa, góc so le trong A4 và B2 bằng nhau. Dựa vào tính chất này, ta có thể kết luận rằng:
- Các góc so le trong còn lại là A1 và B3 cũng bằng nhau
- Các cặp góc đồng vị A1 và B1, A2 và B2, A3 và B3, A4 và B4 đều bằng nhau.
3. Dấu hiệu nhận diện và phương pháp chứng minh hai góc đồng vị
Để nhận biết và chứng minh hai góc đồng vị, ta cần dựa vào các dấu hiệu sau đây:
Khi đường thẳng c cắt hai đường thẳng a và b, các cặp góc đồng vị có những đặc điểm sau:
- Hai góc không được chia sẻ chung đỉnh
- Hai góc đồng vị nằm cùng phía so với đường thẳng c và có cùng vị trí trên hai đường thẳng a và b
Bài tập thực hành:
Bài 1: Xác định xem các phát biểu dưới đây là đúng hay sai
a. Hai góc có tổng số đo là 180° là hai góc đồng vị
b. Khi một đường thẳng z cắt hai đường thẳng x và y, sẽ tạo ra bốn cặp góc đồng vị
Trả lời:
a. Phát biểu này không chính xác. Hai góc có tổng số đo bằng 180° được gọi là góc bù nhau.
b. Phát biểu này là chính xác.
Bài 2:
A. Góc A1 và góc B3
B. Góc A3 và góc B1
C. Góc A4 và góc B4
D. Góc A3 và góc B2
Trả lời: Đáp án chính xác là đáp án C. Góc A4 và góc B4 là hai góc đồng vị.
4. Góc đồng vị được hình thành khi một đường thẳng cắt hai đường thẳng song song.
- Hai đường thẳng song song là những đường thẳng không giao nhau. Khi hai đường thẳng a và b song song, chúng ta ký hiệu là a//b. Điều này có nghĩa là đường thẳng a song song với đường thẳng b hoặc ngược lại.
- Dấu hiệu nhận biết hai đường thẳng song song: Nếu một đường thẳng c cắt hai đường thẳng a và b, và trong các góc tạo thành có một cặp góc so le trong hoặc góc đồng vị bằng nhau, thì a và b là hai đường thẳng song song.
- Tiên đề Ơ - clit về đường thẳng song song: Qua một điểm ngoài một đường thẳng chỉ có duy nhất một đường thẳng song song với đường thẳng đó.
- Đặc điểm của hai đường thẳng song song: Khi một đường thẳng cắt hai đường thẳng song song thì:
+ Các góc so le trong sẽ bằng nhau
+ Các góc đồng vị sẽ bằng nhau
+ Các góc cùng phía sẽ bù nhau
5. Các loại bài tập thường gặp liên quan đến góc đồng vị
5.1. Dạng 1: Xác định hai góc đồng vị
Phương pháp giải: Sử dụng định nghĩa và các dấu hiệu nhận biết để xác định hai góc đồng vị.
5.2. Dạng 2: Tính giá trị các góc được tạo ra khi một đường thẳng cắt hai đường thẳng khác
Phương pháp giải: Áp dụng các tính chất liên quan đến góc đồng vị, góc kề bù, góc so le trong, góc đối đỉnh và phân tích đề bài để tìm ra kết quả chính xác.
Bài tập ứng dụng:
Bài 1: Quan sát hình dưới đây. Biết a//b, góc BAC = 50o, góc BCA = 85o. Tính giá trị các góc: ABC, CDE, CED.
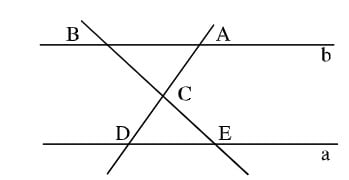
Trả lời:
Vì góc BAC và góc CDE là hai góc so le trong và a//b nên góc CDE = góc BAC = 50o.
Trong tam giác ABC, tổng ba góc là 180o. Vì góc BAC = 50o và góc BCA = 85o, nên góc ABC = 180o - 50o - 85o = 45o.
Góc CED và góc ABC là hai góc so le trong, do đó góc CED = 45o.
Bài 2: Quan sát hình dưới đây và tính các góc chưa biết.
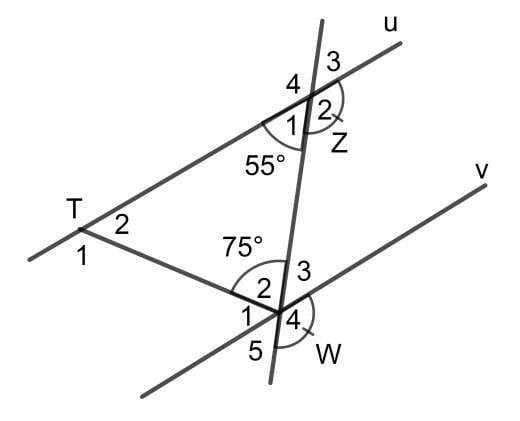
Trả lời:
Góc Z1 và góc Z4 là hai góc kề bù, vì vậy góc Z4 = 180o - 55o = 125o.
Góc Z2 và góc Z4, góc Z1 và góc Z3 là các cặp góc đối đỉnh, do đó góc Z2 = góc Z4 = 125o và góc Z3 = góc Z1 = 55o.
Các cặp góc W3 và Z3, W4 và Z2 là các cặp góc đồng vị. Vì u//v nên góc W3 = góc Z3 = 55o và góc W4 = góc Z2 = 125o.
Góc W5 và góc W3 là hai góc đối đỉnh, vì vậy góc W5 = góc W3 = 55o.
Tổng các góc W1, W2 và W3 là 180o, do đó góc W1 = 180o - 75o - 55o = 50o.
Góc T2 và góc W1 là hai góc so le trong, vì vậy góc T2 = góc W1 = 50o.
Góc T1 và góc T2 là hai góc kề bù, do đó góc T1 = 180o - 50o = 130o.
5.3. Dạng 3: Bài tập tổng hợp liên quan đến hai góc đồng vị
Phương pháp giải: Dựa trên yêu cầu của bài toán, phân tích và lựa chọn phương pháp giải phù hợp để đạt kết quả chính xác nhất.
6. Các loại bài toán về góc thường gặp
- Dạng 1: Xác định các cặp góc so le trong, góc đồng vị, và góc cùng phía
- Dạng 2: Tính giá trị của góc khi biết một trong bốn góc được tạo bởi hai đường thẳng
- Dạng 3: Xác định các cặp góc bằng nhau, góc bù nhau, góc phụ nhau, góc kề bù, v.v.
- Dạng 4: Xác định vị trí cụ thể của các góc.
- Dạng 5: Chứng minh vị trí của các góc dựa trên các định lý hoặc tính chất.
- Dạng 6: Tìm các cặp góc đáp ứng điều kiện đề bài đưa ra
- Dạng 7: Áp dụng vị trí của góc để giải quyết các bài toán chứng minh hai đường thẳng song song hoặc hai đường thẳng vuông góc.
- Dạng 8: Ứng dụng vị trí của góc trong các bài toán khác như bài toán về tam giác, hình vuông, hình chữ nhật, v.v.
Bài tập ứng dụng:
Bài 1: Một đường thẳng cắt hai đường thẳng khác tạo ra các cặp góc so le trong, góc cùng phía, v.v. Nếu có một cặp góc so le trong bằng nhau, các khẳng định sau đây là đúng hay sai?
a. Các cặp góc so le trong còn lại cũng bằng nhau.
b. Các cặp góc đồng vị là bằng nhau
c. Các cặp góc cùng phía là bù nhau
Bài 2:
a. Vẽ hình theo mô tả sau: hai đường thẳng mn và pq không giao nhau. Đường thẳng xy cắt mn tại U và pq tại V. Biết rằng U1 và V1 là góc cùng phía, U2 và V1 là góc đồng vị, U1 và V2 là góc so le.
b. Nếu góc U1 và V2 đều bằng 36o, hãy xác định số đo của các góc U2 và V1.
Trên đây là phần giới thiệu từ Mytour về chủ đề Góc đồng vị là gì? Cách chứng minh hai góc đồng vị?. Hy vọng những thông tin này sẽ giúp ích cho bạn.
