Góc giữa hai mặt phẳng: Định nghĩa, cách xác định và Bài tập (có đáp án) Tổng ôn Toán 11

Góc giữa hai mặt phẳng là một trong những kiến thức quan trọng trong chương trình học lớp 11 và lớp 12. Để giải các dạng bài tập liên quan đến góc giữa hai đường thẳng, học sinh cần hiểu sâu về lý thuyết và công thức tính góc giữa hai mặt phẳng.

Góc giữa hai mặt phẳng là góc được tạo ra bởi hai đường thẳng với hai mặt phẳng, đơn giản là góc giữa đường thẳng và mặt phẳng. Trong không gian ba chiều, góc giữa hai mặt phẳng còn được gọi là góc khối và được giới hạn bởi hai mặt phẳng. Dưới đây là toàn bộ kiến thức về góc giữa hai mặt phẳng mời các bạn theo dõi. Ngoài ra, bạn cũng có thể xem thêm về Công thức truy hồi.

Góc giữa hai mặt phẳng

• 1. Định nghĩa góc giữa hai mặt phẳng
• 2. Cách xác định góc giữa hai mặt phẳng
• 3. Công thức tính góc giữa hai mặt phẳng 
• 4. Phương pháp tính góc giữa hai mặt phẳng
• 5. Bài tập áp dụng
• 6. Bài tập tự luyện 

1. Khái niệm về góc giữa hai mặt phẳng

- Định nghĩa: Góc giữa hai mặt phẳng là gì? Góc giữa hai mặt phẳng được tạo ra bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Trong không gian ba chiều, góc giữa hai mặt phẳng còn được gọi là ‘góc khối’, là phần không gian được giới hạn bởi hai mặt phẳng. Để đo góc giữa hai mặt phẳng, ta đo góc giữa hai đường thẳng trên mặt hai mặt phẳng có cùng đường giao của hai mặt phẳng.

- Tính chất: Từ định nghĩa trên, ta có:

• Góc giữa hai mặt phẳng song song bằng 0 độ,
• Góc giữa hai mặt phẳng trùng nhau bằng 0 độ.

2. Phương pháp xác định góc giữa hai mặt phẳng

Để xác định góc giữa hai mặt phẳng một cách chính xác, bạn có thể áp dụng các cách sau đây:

Gọi P là mặt phẳng 1, Q là mặt phẳng 2

Trường hợp 1: Hai mặt phẳng (P), (Q) song song hoặc trùng nhau, góc giữa hai mặt phẳng bằng 0,

Trường hợp 2: Hai mặt phẳng (P), (Q) không song song hoặc trùng nhau.

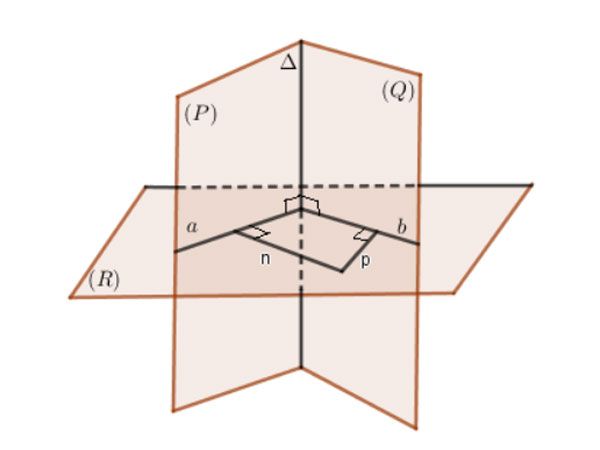
Phương pháp 1: Vẽ hai đường thẳng n và p vuông góc lần lượt với hai mặt phẳng (P), (Q). Khi đó, góc giữa hai mặt phẳng (P), (Q) là góc giữa hai đường thẳng n và p.

Phương pháp 2: Để xác định góc giữa hai mặt phẳng đầu tiên, bạn cần xác định giao tuyến Δ∆của hai mặt phẳng (P) và (Q). Tiếp theo, bạn tìm một mặt phẳng (R) vuông góc với giao tuyến Δ∆của hai mặt phẳng (P), (Q) và cắt hai mặt phẳng tại các giao tuyến a, b.

⇒ Góc giữa hai mặt phẳng (P), (Q) là góc giữa a và b.

3. Công thức tính góc giữa hai mặt phẳng

4. Phương pháp tính góc giữa hai mặt phẳng

Có hai cách bạn có thể sử dụng để tính góc giữa hai mặt phẳng:

Cách 1: Áp dụng các công thức trong tam giác vuông, định lý về hàm số sin, và hàm số cos.

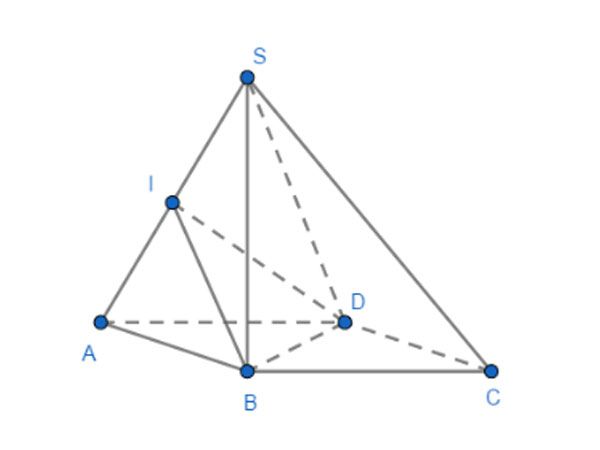
Ví dụ 1: Trong hình chóp tứ giác đều S.ABCD với đáy là ABCD và các cạnh đáy có độ dài a, SA = SB = SC = SD = a. Tính cosin của góc giữa hai mặt phẳng (SAB) và (SAD).

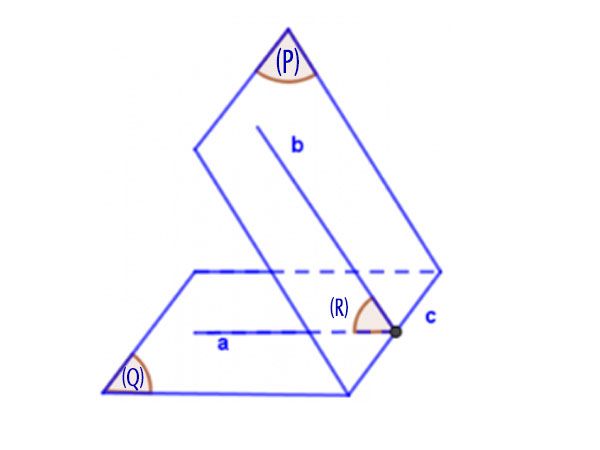
Cách 2: Dựng một mặt phẳng phụ (R) vuông góc với đường giao của mặt phẳng c, trong đó mặt phẳng (Q) gặp (R) tại điểm a và mặt phẳng (P) gặp (R) tại điểm b.

Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh SA=a và vuông góc với đáy. Tính góc giữa hai mặt phẳng (SBC) và (ABCD), cũng như góc giữa mặt phẳng (SBD) và mặt phẳng (ABCD).

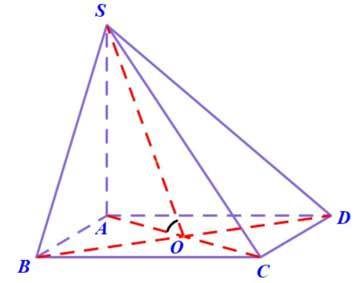
Đáp án gợi ý

Để tính góc giữa hai mặt phẳng (SBC) và (ABCD), ta áp dụng phương pháp thứ 2.

- Giao tuyến của hai mặt phẳng (SBC) và (ABCD) là BC.

- Bây giờ, cần tìm một mặt phẳng vuông góc với giao tuyến BC. Nếu bạn nhận ra rằng mặt phẳng (SAB) chính là mặt phẳng cần tìm, thì tốt. Nếu chưa, hãy chú ý hai điều sau:

+ Để có một mặt phẳng vuông góc với BC, cần tìm mặt phẳng nào chứa hai đường thẳng cắt nhau và đều vuông góc với BC.

+ Đường thẳng BC vuông góc với các đường thẳng nào (bao gồm cả SA và AB).

- Tiếp theo, sau khi có mặt phẳng (SAB), ta tìm giao tuyến của nó với hai mặt phẳng ban đầu, tức là các đường thẳng AB và SB.

- Cuối cùng, ta tính góc giữa hai đường thẳng AB và SB, tức góc SBA. Hãy tự tính xem góc này có bao nhiêu độ.

Để tính góc giữa hai mặt phẳng (SBD) và (ABCD), làm theo các bước tương tự như trên. Gợi ý: góc giữa hai mặt phẳng này chính là góc SOA.

5. Bài tập thực hành

Câu 1: Trong tam giác ABC vuông tại A, AB = a nằm trong mặt phẳng (P), AC = a√2 và tạo với (P) góc 60°. Khẳng định nào sau đây là đúng?

A. Góc (ABC) và (P) là 45°
B. Góc (BC) và (P) là 30°
C. Góc (BC) và (P) là 45°

Câu 2: Trong tứ diện ABCD với AC = AD và BC = BD. I là trung điểm của CD. Khẳng định nào sau đây là sai?

A. Góc giữa (ACD) và (BCD) là ∠AIB
B. (BCD) vuông góc (AIB)
C. Góc giữa (ABC) và (ABD) là ∠CBD
D. (ACD) vuông góc (AIB)
Câu 3: Trong hình chóp S. ABC, SA ⊥ (ABC) và AB ⊥ BC. Gọi I là trung điểm BC. Góc giữa (SBC) và (ABC) là góc nào sau đây?

A. Góc SBA.
B. Góc SCA.
C. Góc SCB.
D. Góc SIA.

Câu 4: Trong hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD), O là tâm hình vuông ABCD. Khẳng định nào sau đây là sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA
D. (SAC) ⊥ (SBD)

Câu 5: Trong hình lập phương ABCD.A1B1C1D1 . Gọi α là góc giữa hai mặt phẳng (A1D1CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?

A. α = 45°
B. α = 30°
C. α = 60°
D. α = 90°

Câu 6: Trong hình chóp S.ABCD với đáy là hình vuông có tâm O và SA ⊥ (ABCD). Khẳng định nào sau đây là sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc ∠ABS
B. (SAC) ⊥ (SBD)
C. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc ∠SOA
D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc ∠SDA

Câu 7. Trong hình chóp S.ABCD với đáy là hình thoi cạnh a và góc ∠ABC = 60°. Các cạnh SA ; SB ; SC đều bằng a(√3/2) . Gọi φ là góc của hai mặt phẳng (SAC) và (ABCD) . Giá trị tanφ bằng bao nhiêu?

A. 2√5
B. 3√5
C. 5√3
D. Đáp án khác

Câu 8: Trong hình chóp S.ABCD với đáy là hình thang vuông tại A và D. AB = 2a; AD = DC = a. Cạnh bên SA vuông góc với đáy và SA = a√2. Chọn khẳng định sai trong các khẳng định sau?

A. (SBC) ⊥ (SAC)
B. Giao tuyến của (SAB) và (SCD) song song với AB
C. (SDC) tạo với (BCD) một góc 60°
D. (SBC) tạo với đáy một góc 45°

Câu 9: Trong hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA’ = a; AD = 2a. Gọi α là góc giữa đường chéo A’C và đáy ABCD. Tính α .

A. α ≈ 20°45'
B. α ≈ 24°5'
C. α ≈ 30°18'
D. α ≈ 25°48'

Câu 10: Trong hình lập phương ABCD.A'B'C'D'. Xét mặt phẳng (A’BD). Trong các mệnh đề sau mệnh đề nào đúng?

A. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√2 .
B. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√3
C. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc vào kích thước của hình lập phương.
D. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.

Câu 11: Trong hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.

A. 30°
B. 45°
C. 60°
D. 75°

Câu 12. Trong hình chóp tứ giác đều có cạnh đáy bằng a√2 và chiều cao bằng a√2/2 . Tính số đo của góc giữa mặt bên và mặt đáy.

A. 30°
B. 45°
C. 60°
D. 75°

Câu 12: Trong hình chóp S.ABCD có đáyABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu?

A. 30°
B. 45°
C. 90°
D. 60°

Câu 13: Trong hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD); SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60°.

A. x = 3a/2
B. x = a/2
C. x = a
D. x = 2a

Câu 14: Trong hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC). Gọi E; F lần lượt là trung điểm của các cạnh AB và AC . Góc giữa hai mặt phẳng (SEF) và (SBC) là :

A. ∠CSF
B. ∠BSF
C. ∠BSE
D. ∠CSE

Câu 15: Trong tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B và C lần lượt lấy D; E nằm trên cùng một phía đối với (P) sao cho BD = a(√3/2), CE = a√3 . Góc giữa (P) và (ADE) bằng bao nhiêu?

A. 30°
B. 60°
C. 90°
D. 45°

Câu 16.  Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một đường thẳng cố định.
D. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.

Câu 17. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hai mặt phẳng khi vuông góc với một mặt phẳng khác cũng vuông góc với nhau.
B. Một đường thẳng có thể chỉ đi qua một mặt phẳng vuông góc với một mặt phẳng khác.
C. Các mặt phẳng đi qua một điểm cố định và vuông góc với một mặt phẳng khác sẽ luôn tạo thành một đường thẳng cố định.
D. Hai mặt phẳng song song với một mặt phẳng thứ ba cũng song song với nhau.

Câu 18: Trong các câu sau, câu nào đúng?

A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.

Câu 19. Trong các câu sau, câu nào đúng?

A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
D. Nếu hình hộp có năm mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.

Câu 20. Trong các câu sau, câu nào đúng?

A. Hai mặt phẳng khi song song với một mặt phẳng khác cũng song song với nhau.
B. Một đường thẳng có thể chỉ đi qua một mặt phẳng vuông góc với một mặt phẳng khác.
C. Chỉ có duy nhất một mặt phẳng đi qua một điểm cố định và vuông góc với hai mặt
phẳng cắt nhau cho trước.
D. Hai mặt phẳng khi vuông góc với một mặt phẳng thứ ba cũng vuông góc với nhau.

6. Bài tập tự luyện

1) Chứng minh rằng (SBC) vuông góc với (SAB) và (SCD) vuông góc với (SAD)

2) Tính góc giữa (SCD) và (ABCD)

Bài 2 : Hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và vuông góc (ABC).

1) Xác định chân đường cao H kẻ từ S của hình chóp .

2) Chứng minh rằng (SBC) vuông góc với (SAC) .

3) Gọi I là trung điểm SC, chứng minh rằng (ABI) vuông góc với (SBC)

Bài 3 : Cho hình chóp tam giác đều S.ABC có cạnh đáy là a. Gọi I là trung điểm BC

1) Chứng minh rằng (SBC) vuông góc với (SAI) .

2) Biết góc giữa (SBC) và (ABC) là 60 độ. Tính chiều cao SH của hình chóp.

Bài 4 : Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy cùng bằng a.

1) Tính chiều cao của hình chóp.

2) M là trung điểm SC. Chứng minh rằng (MBD) vuông góc với (SAC).

3) Tính góc giữa mặt bên và mặt đáy của hình chóp.

Bài 5: Hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = 2a ,

AD = CD =a , cạnh SA vuông góc với đáy và SA = a.

1) Chứng minh rằng (SAD) vuông góc với (SCD) và (SAC) vuông góc với (SBC).

2) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD). Tính tan φ .

Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . SA = a và SA vuông

góc (ABCD). Tính góc giữa (SBC) và (SCD)

1) Chứng minh rằng (SBD) vuông góc với (ABCD)

2) Chứng minh tam giác SBD vuông .

Bài 8 : Cho tam giác đều ABC cạnh a , I là trung điểm BC và D là điểm đối xứng với A

1) (SAB) vuông góc (SAC) .

2) (SBC) vuông góc (SAD)

1) Chứng minh rằng (SAC) vuông góc với (ABCD) và SB vuông góc BC .

2) Tính tan của góc giữa (SBD) và (ABCD) .

Bài 10 : Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc nhau . Gọi I là trung điểm AB .

1) Chứng minh rằng (SAD) vuông góc với (SAB) .

2) Tính góc giữa SD và (ABCD) .

3) Gọi F là trung điểm AD . Chứng minh rằng (SCF) vuông góc với (SID) .

Bài 11

Cho hình chóp S.ABC, SA vuông góc ABC

a) Xác định góc giữa (ABC) và (SBC)

b) Giả sử tam giác ABC vuông tại B xác định góc giữa hai mp (ABC) và (SBC)

Bài 12: Cho hình chóp tứ giác đều S. ABCD đáy ABCD là hình vuông cạnh a, SA=SB=SC=SD=a. Tính cosin của góc giữa (SAB) và (SAD).