Góc vuông

Trong hình học cơ bản, tính chất góc vuông đề cập đến mối liên hệ giữa hai đường thẳng khi chúng cắt nhau tạo thành một góc có độ lớn 90 độ. Tính chất này cũng có thể áp dụng cho các hình dạng hình học khác.

Một đường thẳng được coi là vuông góc với một đường thẳng khác nếu hai đường thẳng này cắt nhau tạo thành góc vuông. Cụ thể, nếu đường thẳng thứ nhất vuông góc với đường thẳng thứ hai thì (1) hai đường thẳng phải cắt nhau và (2) tại điểm giao, góc bẹt trên một phía của đường thẳng thứ nhất bị đường thẳng thứ hai chia thành hai góc bằng nhau. Tính vuông góc mang tính đối xứng, tức là nếu đường thẳng thứ nhất vuông góc với đường thẳng thứ hai, thì ngược lại cũng đúng. Do đó, hai đường thẳng có thể được mô tả là vuông góc với nhau mà không cần chú trọng thứ tự.

Tính vuông góc có thể mở rộng cho các đoạn thẳng và tia. Ví dụ, đoạn thẳng $\stackrel{¯<!--\; ¯\; -->}{AB}$ vuông góc với đoạn thẳng $\stackrel{¯<!--\; ¯\; -->}{CD}$ nếu, khi mở rộng cả hai đoạn thẳng ra hai phía để tạo thành đường thẳng, hai đường thẳng này sẽ tự động tuân theo định nghĩa vuông góc đã nêu. Ký hiệu, $\stackrel{¯<!--\; ¯\; -->}{AB}\perp <!--\; \perp \; -->\stackrel{¯<!--\; ¯\; -->}{CD}$ có nghĩa là đoạn thẳng AB vuông góc với đoạn thẳng CD.

Một đường thẳng được gọi là vuông góc với mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó và cắt với đường thẳng này. Định nghĩa này dựa trên định nghĩa hai đường thẳng vuông góc với nhau.

Hai mặt phẳng trong không gian được coi là vuông góc nếu góc tạo bởi chúng là góc vuông (90 độ).

Tính vuông góc là một trường hợp đặc biệt của khái niệm toán học rộng hơn, đó là tính trực giao. Trong toán học nâng cao, từ 'vuông góc' thường được dùng để chỉ các điều kiện trực giao phức tạp hơn, như giữa các mặt phẳng và các vectơ trực chuẩn của chúng.

Quan hệ vuông góc trong mặt phẳng

Hai đường thẳng vuông góc với nhau

Chỉ có duy nhất một đường thẳng có thể đi qua một điểm và vuông góc với một đường thẳng đã cho.

Vẽ hai đường vuông góc

Để vẽ một đường thẳng vuông góc với đường thẳng AB qua điểm P bằng thước kẻ và compa, thực hiện các bước sau (xem hình bên trái):

• Bước 1 (đỏ): Vẽ một đường tròn với tâm tại P có bán kính tùy chọn sao cho đường tròn cắt đường thẳng AB tại hai điểm A' và B', cách đều từ P.
• Bước 2 (lục): Vẽ hai đường tròn có tâm lần lượt tại A' và B' với bán kính bằng nhau. Gọi Q và R là các giao điểm của hai đường tròn này.
• Bước 3 (lam): Kết nối Q và R để tạo ra đường thẳng PQ mong muốn.

Để chứng minh PQ vuông góc với AB, áp dụng định lý tam giác đồng dạng CCC cho hai tam giác QPA' và QPB' để chứng minh rằng hai góc OPA' và OPB' bằng nhau. Tiếp theo, sử dụng định lý tam giác đồng dạng CGC cho hai tam giác OPA' và OPB' để xác định rằng hai góc POA và POB cũng bằng nhau.

Để vẽ một đường thẳng vuông góc với một đường thẳng tại hoặc qua điểm P, sử dụng định lý Thales, xem hình minh họa bên cạnh.

Có thể sử dụng định lý Pytago làm cơ sở để dựng góc vuông. Ví dụ, dùng ba đoạn thước với tỷ lệ 3:4:5 để tạo tam giác vuông. Phương pháp này rất tiện lợi cho việc sắp xếp các đồ vật hoặc xác định vị trí trên diện tích lớn như mảnh đất hoặc khu vườn, khi không yêu cầu độ chính xác cao. Tam giác vuông này có thể được tái sử dụng khi cần.

Chân đường vuông góc - hình chiếu vuông góc của một điểm lên đường thẳng

Từ chân thường đi kèm với khái niệm vuông góc. Ví dụ về cách sử dụng từ này được thể hiện trong hình minh họa trên và phần chú thích của nó. Hình vẽ có thể có hướng bất kỳ. Chân đường vuông góc không nhất thiết phải nằm ở đáy. Chân đường vuông góc cũng được gọi là hình chiếu vuông góc của một điểm lên đường thẳng.

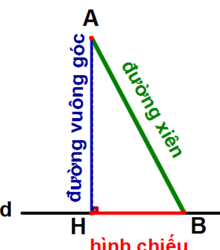
Đường vuông góc, đường xiên và hình chiếu của đường xiên

Trong tất cả các đoạn thẳng từ một điểm ngoài một đường thẳng cắt đường thẳng đó, đoạn vuông góc là đoạn thẳng ngắn nhất và duy nhất. Các đoạn thẳng khác được gọi là đường xiên.

Đoạn thẳng giữa chân đường vuông góc và điểm giao của đường xiên với đường thẳng được gọi là hình chiếu của đường xiên lên đường thẳng đó.

Khi xét các đường xiên từ một điểm ngoài đường thẳng đến đường thẳng đó:

• Đường xiên dài hơn (hoặc ngắn hơn) sẽ có hình chiếu dài hơn (hoặc ngắn hơn) và ngược lại
• Hai đường xiên bằng nhau sẽ có hình chiếu bằng nhau và ngược lại

Quan hệ vuông góc trong không gian ba chiều

Đường thẳng vuông góc với một mặt phẳng

Một đường thẳng được coi là vuông góc với một mặt phẳng khi nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Nếu một đường thẳng vuông góc với hai đường thẳng giao nhau trong cùng một mặt phẳng, thì đường thẳng đó cũng vuông góc với mặt phẳng chứa hai đường thẳng này.

Có duy nhất một đường thẳng đi qua một điểm ngoài mặt phẳng và vuông góc với mặt phẳng đó.

Có duy nhất một mặt phẳng đi qua một điểm ngoài đường thẳng và vuông góc với đường thẳng đó.

Chiếu vuông góc

Khi đường thẳng (d) vuông góc với mặt phẳng (P), phép chiếu song song theo hướng của (d) lên mặt phẳng (P) được gọi là chiếu vuông góc.

Hình chiếu vuông góc là kết quả của phép chiếu vuông góc.

Khi không chỉ định rõ loại phép chiếu, mặc định đó là phép chiếu vuông góc.

Đường thẳng vuông góc trong không gian

Trong không gian, hai đường thẳng vuông góc với nhau có thể giao nhau hoặc cắt nhau theo cách chéo.

Khi đường thẳng (a) không vuông góc với mặt phẳng (P) và đường thẳng $\left(d\right)\subset <!--\; \subset \; -->\left(P\right)$, thì $\left(a\right)\perp <!--\; \perp \; -->\left(b\right)\iff <!--\; \iff \; -->\left(a\right)\perp <!--\; \perp \; -->\left(b^{\prime }\right)$ với (b') là hình chiếu của (a) trên (P).

Hai mặt phẳng vuông góc

Hai mặt phẳng vuông góc khi và chỉ khi một trong số chúng chứa một đường thẳng vuông góc với mặt phẳng còn lại.

Khi hai mặt phẳng vuông góc với nhau, bất kỳ đường thẳng nào nằm trong một trong hai mặt phẳng và vuông góc với giao tuyến của chúng đều vuông góc với mặt phẳng còn lại.

Khi hai mặt phẳng (P) và (Q) vuông góc với nhau, thì đường thẳng đi qua một điểm trong mặt phẳng (P) và vuông góc với mặt phẳng (Q) sẽ luôn nằm trong mặt phẳng (P).

Nếu hai mặt phẳng cắt nhau và đều vuông góc với một mặt phẳng thứ ba, thì giao tuyến của chúng sẽ vuông góc với mặt phẳng thứ ba đó.

Có đúng một mặt phẳng có thể đi qua một đường thẳng và vuông góc với một mặt phẳng không vuông góc với đường thẳng đó.

• Các thành phần pháp tuyến và tiếp tuyến
• Pháp tuyến

• Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (ấn bản 2), New York: Barnes & Noble, LCCN 52-13504
• Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
• Phan Đức Chính và cộng sự, Sách giáo khoa Toán 7 - tập 1, Nhà xuất bản giáo dục Việt Nam
• Phan Đức Chính và cộng sự, Sách giáo khoa Toán 7 - tập 2, Nhà xuất bản giáo dục Việt Nam
• Trần Văn Hạo và cộng sự, Sách giáo khoa Hình học 11, Nhà xuất bản giáo dục Việt Nam
• Đoàn Quỳnh và cộng sự, Sách giáo khoa Hình học 11 Nâng cao, Nhà xuất bản giáo dục Việt Nam

Liên kết bên ngoài

• Định nghĩa: đường vuông góc với hoạt hình tương tác.
• Cách vẽ đường phân giác vuông góc của một đoạn thẳng bằng compa và thước kẻ (trình diễn hoạt hình).
• Cách vẽ đường vuông góc tại điểm kết thúc của một tia bằng compa và thước kẻ (trình diễn hoạt hình).