Đặc biệt là chưa ai từng chứng minh được định lý này theo cách như vậy, ngay cả Albert Einstein.
Thời học phổ thông, ai trong chúng ta cũng đã từng phải giải bài toán hình học không gian. Khi giải bài toán này, chắc chắn ai cũng ít nhất một lần gặp tình huống: khi đang vẽ hình thì hết giấy.
Tất cả những trường hợp như vậy thường liên quan đến một chiếc tam giác "đột biến", với hai cạnh dài bất thường, khiến cho khi vẽ đến mép giấy mà chúng vẫn không gặp nhau. Trong tình huống này, bạn sẽ xử lý như thế nào?

Ảnh minh họa.
Nhiều học sinh - rất sáng tạo - sẽ vẽ tiếp hình sang một chiều không gian khác, tức là mặt sau của tờ giấy. Một số khác sẽ lấy thêm một tờ giấy nữa, đặt dưới tờ giấy cũ để vẽ tiếp cho đủ hình. Hoặc nếu cần gấp, bạn cũng có thể vẽ tam giác tràn ra mặt bàn.
Dù vậy, có một số người sẽ cho rằng: Tại sao không dừng lại ở việc vẽ chiếc tam giác "đột biến" đó? Cứ vẽ hết giấy là được, không cần phải cố chấp. Thậm chí, nếu bạn không vẽ hết hình trong mặt giấy, lời giải của bạn sẽ không chính xác.
Tuy nhiên, một nghiên cứu mới đăng trên tạp chí American Mathematical Monthly có thể khiến họ phải xem xét lại. Đôi khi, phần tam giác nằm ngoài tờ giấy lại ẩn chứa những bí ẩn bất ngờ trong toán học.
Cụ thể, trong trường hợp này, hai học sinh trung học tại Mỹ đã phát hiện ra một cách chứng minh định lý Pytago, vốn được coi là "bất khả" suốt hơn 2.500 năm kể từ khi nó được đưa ra.

Ảnh minh họa.
Chưa ai từng chứng minh định lý Pytago theo cách này, ngay cả Albert Einstein
Định lý Pytago được đặt theo tên nhà toán học Hy Lạp cổ đại Pythagoras (570-495 TCN) - người đầu tiên chứng minh định lý này, mặc dù đã có những bằng chứng cho thấy các nền văn minh cổ đại khác như Babylon, Ấn Độ, Lưỡng Hà và Trung Quốc cũng đã phát hiện ra nó độc lập:
Định lý nói rằng trong một tam giác vuông, bình phương của cạnh huyền luôn bằng tổng bình phương độ dài của hai cạnh góc vuông. Nếu độ dài của hai cạnh góc vuông là a và b, và cạnh huyền là c, thì Định lý Pytago được biểu diễn bằng công thức:
𝑐2 = 𝑎2 + 𝑏2
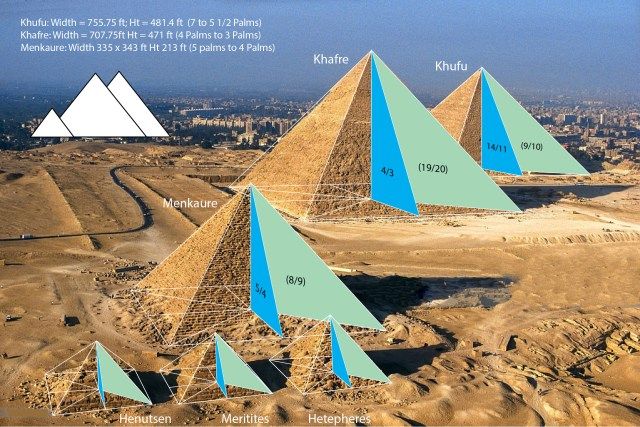
Nếu không có Định lý Pytago, người Ai Cập cổ đại sẽ không thể xây dựng được kim tự tháp.
Dù chỉ là một công thức đơn giản, nhưng nếu không biết đến Định lý Pytago, người Ai Cập cổ đại không thể xây kim tự tháp, người Babylon không thể xác định vị trí của các ngôi sao, và người Trung Quốc không thể phân chia ruộng đất.
Định lý này còn là nền tảng cho nhiều trường phái toán học như hình học không gian, hình học phi Euclid và hình học vi phân - nếu thiếu nó, hoặc nếu nó được chứng minh là sai, thì gần như toàn bộ nhánh hình học mà nhân loại biết đến ngày nay sẽ sụp đổ.
Việc chứng minh Định lý Pytago là điều cực kỳ quan trọng. Vì vậy, từ những năm 500 trước Công Nguyên, nhà toán học Hy Lạp cổ đại Pythagoras đã nhận trách nhiệm này và ghi tên mình vào lịch sử lần đầu tiên.
Ông đã chứng minh Định lý Pytago bằng một phương pháp rất đơn giản:
Ảnh minh họa.
Vẽ một hình vuông có độ dài cạnh là a+b. Sau đó, ở mỗi góc của hình vuông, tiếp tục vẽ 4 hình tam giác bằng nhau, với cạnh là a và b. Các tam giác này đều là tam giác vuông, có cạnh huyền là c, và tạo thành một khoảng trống bên trong hình vuông có diện tích là c2.
Bằng cách sắp xếp lại vị trí của 4 tam giác, Pythagoras đã tạo ra hai khoảng trống mới là hai hình vuông có cạnh a và b. Tổng diện tích của hai khoảng trống đó là a2 + b2, và dĩ nhiên phải bằng diện tích khoảng trống ban đầu c2.
Cách chứng minh này sẽ được tìm thấy trong sách giáo khoa Toán lớp 7 ở bậc trung học cơ sở. Tuy nhiên, còn một cách chứng minh khác về Định lý Pytago mà bạn có thể chưa từng học, đó chính là giải pháp mà Albert Einstein đưa ra khi mới 11 tuổi.
Khi đó, Einstein nhận thấy rằng nếu cậu hạ một đường cao AD vuông góc với cạnh huyền BC của tam giác vuông ABC, cậu sẽ có được 2 tam giác vuông đồng dạng với tam giác vuông ABC. Bây giờ, chỉ cần vẽ ra bên ngoài tam giác vuông ABC các hình vuông có cạnh tương ứng, Einstein sẽ thu được 3 hình vuông với diện tích a2, b2 và c2.
Vì tỉ lệ diện tích giữa một tam giác vuông và hình vuông dựng trên cạnh huyền của nó là bằng nhau với các tam giác đồng dạng, chúng ta cũng sẽ có 𝑐2 = 𝑎2 + 𝑏2.
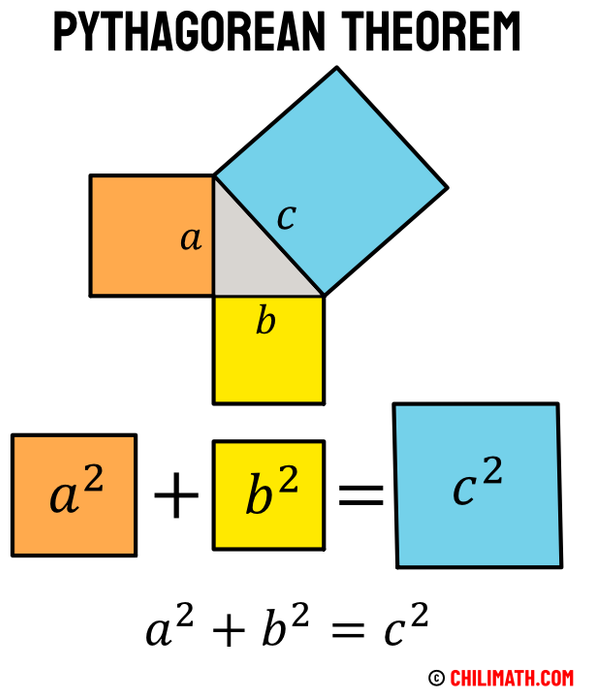
Ảnh minh họa.
Tuy nhiên, đó chỉ là 2 trong số 370 cách chứng minh Định lý Pytago mà các nhà toán học đã tìm ra trong hơn 2.500 năm qua. Từ việc sử dụng đại số, vi tích phân cho đến các cách cắt ghép hình học khác nhau, định lý này có thể được chứng minh bằng nhiều phương pháp từ đơn giản đến phức tạp.
Dù vậy, trong tất cả các lời giải này, không có cách chứng minh nào sử dụng công thức lượng giác. Bởi vì Pytago là một định lý cơ bản trong lượng giác, việc chứng minh nó bằng lượng giác sẽ dẫn đến một cái bẫy ngụy biện logic, gọi là tư duy tuần hoàn, khi chúng ta dùng chính Định lý Pytago để chứng minh nó.
Nhiều nhà toán học đã liên tục gặp thất bại trong việc chứng minh điều này, đến nỗi vào năm 1927, Elisha Loomis, một nhà toán học người Mỹ, đã phải thốt lên rằng: "Không thể có cách nào chứng minh Định lý Pytago bằng lượng giác, vì tất cả công thức lượng giác cơ bản đều phải dựa vào tính đúng đắn của Định lý Pytago".
Tuy nhiên, hóa ra Elisha Loomis đã lầm.
Gần 100 năm sau, hai học sinh trung học này đã phát hiện ra cách chứng minh Định lý Pytago bằng lượng giác
Trong một nghiên cứu mới được công bố trên tạp chí American Mathematical Monthly, hai học sinh Ne'Kiya Jackson và Calcea Johnson từ trường Trung học St. Mary's Academy ở Colorado đã trình bày không chỉ một mà đến 10 cách chứng minh Định lý Pytago bằng lượng giác.

Ne'Kiya Jackson (trái) và Calcea Johnson (phải).
Để thực hiện điều này, Jackson và Johnson đã sử dụng một tam giác vuông ABC như thường lệ. "Cách chứng minh đầu tiên của chúng tôi bắt đầu bằng việc lật tam giác ABC qua cạnh AC để tạo thành một tam giác cân ABB'", bộ đôi đã viết trong bài báo.
Ở bước tiếp theo, họ sẽ dựng tam giác vuông AB'D bằng cách kéo dài cạnh AB tới điểm D sao cho từ D hạ một đường vuông góc xuống B'A.
Chính ở bước này, hãy đảm bảo rằng bạn có đủ giấy, vì AB'D là một tam giác với cạnh dài bất thường, và điểm D rất có thể sẽ vượt ra ngoài mép giấy của bạn.
Tiếp theo, từ điểm B, bạn sẽ hạ một đường vuông góc với BB', cắt B'D tại điểm E. Sau đó, từ E tiếp tục hạ một đường vuông góc cắt AD tại điểm F… Cứ như vậy, bạn sẽ có vô số tam giác đồng dạng có tổng diện tích bằng diện tích tam giác AB'D:
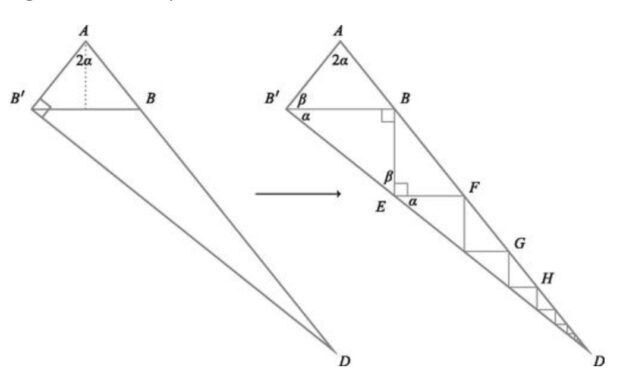
Bây giờ là thời điểm quan trọng:
Jackson và Johnson nhận thấy rằng vì BB' có độ dài 2a và tam giác B'EB đồng dạng với tam giác ABC, họ có thể tính được độ dài cạnh BE là 2a2/b. BF=2A2c/b2. Tương tự, các cạnh FG, GH có thể được xác định bằng 2a4c/b4 và 2a6c/b6…
Khi đó, độ dài cạnh huyền AD sẽ bằng tổng các đoạn thẳng:
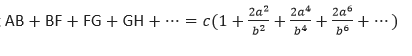
Mà trong tam giác AB'D, chúng ta có:
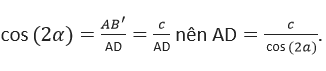
Từ hai công thức trên, ta có thể thiết lập một phương trình:
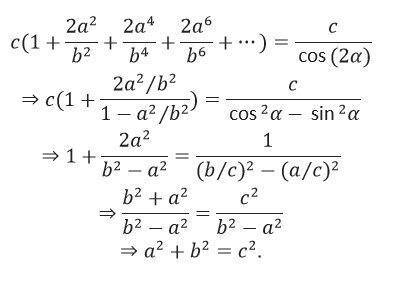
Trong đó, chúng ta sử dụng tổng của một chuỗi hội tụ cơ bản:
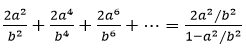
Ngay sau khi công bố, phương pháp chứng minh Định lý Pytago của Jackson và Johnson đã nhanh chóng thu hút sự chú ý của nhiều nhà toán học, trong đó có Álvaro Lozano-Robledo từ Đại học Connecticut.
"Đây là điều mà tôi chưa từng thấy trước đây", Lozano-Robledo nhận xét. Ý tưởng lấp đầy một tam giác lớn bằng vô số tam giác nhỏ và tính độ dài cạnh của nó thông qua một chuỗi hội tụ là một phát minh ngoài sức tưởng tượng đối với học sinh trung học.

Nhà toán học Álvaro Lozano-Robledo từ Đại học Connecticut đã dành lời khen ngợi cho Ne'Kiya Jackson và Calcea Johnson.
"Có nhiều người cho rằng chỉ những ai trải qua nhiều năm nghiên cứu tại trường học hay viện nghiên cứu mới có thể giải quyết được những bài toán mới", Lozano-Robledo chia sẻ. "Nhưng cách giải này chứng minh rằng điều đó hoàn toàn có thể thực hiện ngay cả khi bạn vẫn còn là học sinh trung học".
Không chỉ tìm ra cách chứng minh Định lý Pytago bằng một phương pháp hoàn toàn mới, Jackson và Johnson còn nhấn mạnh vào một ranh giới mong manh của khái niệm lượng giác.
"Học sinh trung học có thể không nhận ra rằng có hai phiên bản lượng giác khác nhau được gán cho cùng một thuật ngữ. Trong tình huống này, cố gắng hiểu lượng giác giống như việc cố hiểu một bức tranh có hai hình ảnh chồng chéo lên nhau", họ nói.
Giải pháp bất ngờ cho Định lý Pytago xuất phát từ việc Jackson và Johnson tách biệt hai biến thể lượng giác và áp dụng một định luật cơ bản khác trong lượng giác, đó là Định luật Sin. Nhờ vậy, bộ đôi đã né tránh những vòng luẩn quẩn mà các nhà toán học trước đó, như Elisha Loomis, đã phải đối mặt khi cố gắng chứng minh Định lý Pytago bằng chính định lý này.

Chưa ai từng chứng minh Định lý Pytago theo cách này, ngay cả Albert Einstein.
"Kết quả của họ đã thu hút sự chú ý từ các học sinh khác đến một góc nhìn mới mẻ và đầy triển vọng", Tổng biên tập tạp chí American Mathematical Monthly, Della Dumbaugh, nhận xét.
"Điều này cũng sẽ mở ra nhiều cuộc thảo luận mới về toán học", Lozano-Robledo nói. "Đó là thời điểm mà những nhà toán học khác có thể sử dụng bài báo này để khái quát hóa chứng minh, phát triển ý tưởng của họ, hoặc đơn giản là áp dụng ý tưởng đó theo những cách khác".
Rõ ràng, một miền đất mới trong toán học đã được khám phá sau khi Jackson và Johnson vẽ ra "tam giác" đột biến. Một tam giác kéo dài ra ngoài mép giấy chứa bên trong là một chuỗi vô tận của các tam giác.
Vì vậy, trong lần tới nếu bạn gặp phải mép giấy khi giải toán hình, hãy thử vẽ tiếp tục xem sao. Biết đâu, bạn sẽ có một phát hiện mới cho riêng mình.
