Khi muốn dự đoán số sự kiện trong một khoảng thời gian nhất định, không thể không sử dụng hàm POISSON. Dưới đây là hướng dẫn chi tiết về cách sử dụng hàm POISSON để ước tính phân phối Poisson.
Mô tả: Hàm POISSON trả về phân phối Poisson, là công cụ cơ bản để xác định số sự kiện xảy ra trong khoảng thời gian xác định, ví dụ như đo lường mật độ xe qua trạm thu phí trong một phút vào cuối tuần. Việc dự đoán này giúp chuẩn bị biện pháp hỗ trợ cụ thể.
Cú pháp: POISSON(x,mean,cumulative).
Trong quá trình sử dụng hàm POISSON:
- x: Đây là số sự kiện, là tham số không thể thiếu.
- mean: Là giá trị cần ước tính (dưới dạng số), là tham số quan trọng.
- cumulative: Xác định dạng thức của giá trị trả về. Có thể là:
+ Nếu cumulative= TRUE => hàm trả về xác suất tích luỹ của phân bố Poisson từ 0 đến x.
+ Nếu cumulative= FALSE: hàm trả về xác suất của phân bố Poisson tại số sự kiện x.
Chú ý:
- Hàm Poission được tính bằng công thức:
+ Khi cumulative= TRUE: hàm trả về xác suất tích luỹ của phân bố Poisson từ 0 đến x.
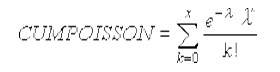
+ Khi cumulative= FALSE: hàm trả về xác suất của phân bố Poisson tại số sự kiện x.
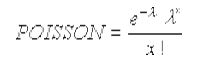
- Nếu x là số thập phân, hàm thực hiện lấy giá trị nguyên của x.
- Cả x và giá trị phải là dạng số, nếu không hàm trả về lỗi #VALUE.
- Trong trường hợp x < 0, hàm sẽ trả về giá trị lỗi #NUM!.
- Nếu mean < 0, hàm sẽ trả về giá trị #NUM!.
Ví dụ:
- Tính Poisson khi cumulative = True: Tại ô bạn muốn tính, nhập công thức: =POISSON(D13,D14,D15).
Để tính, nhập công thức vào ô: =POISSON(D13,D14,D15).
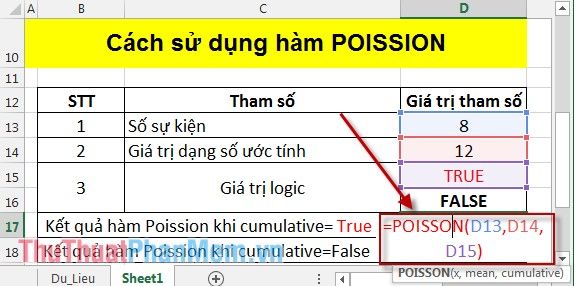
Nhấn Enter để xem kết quả:
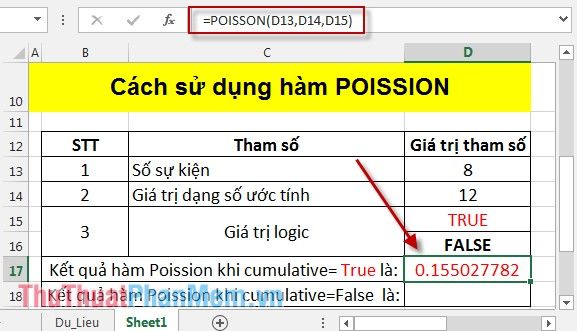
- Tính Poisson khi cumulative = False: Nhập công thức tương ứng vào ô: =POISSON(D13,D14,D16).
Nhấn Enter và bạn sẽ nhận được kết quả ngay lập tức:
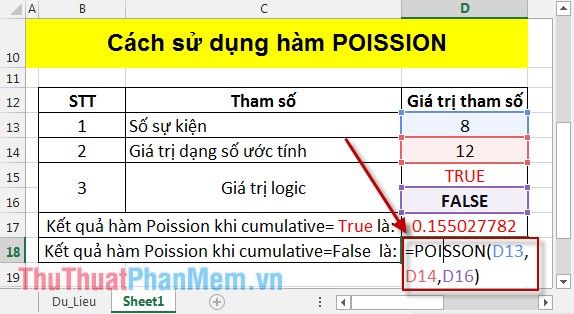
Nhấn Enter, và bạn sẽ nhận được kết quả ngay lập tức:
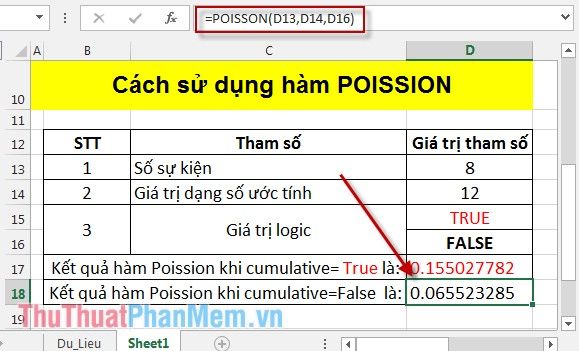
Khi sử dụng hàm Poisson với giá trị cumulative khác nhau, giá trị trả về sẽ thay đổi. Mong rằng hàm Poisson sẽ hỗ trợ bạn dự đoán sự kiện xảy ra trong khoảng thời gian cụ thể.
Chúc bạn đạt được những thành công lớn lao!
