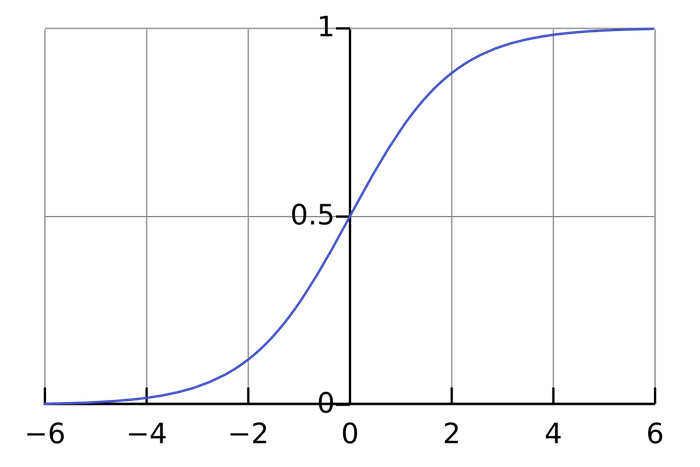
Hàm sigmoid

Hàm sigmoid là một hàm có dạng đường cong hình chữ 'S', thường được gọi là đường cong sigmoid. Ví dụ phổ biến của hàm sigmoid là hàm Logistic, như được trình bày trong hình đầu tiên, với công thức định nghĩa như sau:

$S\left(x\right)=\frac{1}{1+e^{-<!--\; -\; -->x}}=\frac{e^x}{e^x+1}.$

Những hàm sigmoid tiêu chuẩn khác đã được trình bày trong phần ví dụ của bài học này.

Các biến thể đặc biệt của hàm sigmoid bao gồm hàm Gompertz (thường áp dụng trong các mô hình có sự bão hòa ở giá trị lớn của x) và đường cong ogee (được sử dụng trong thiết kế các đập tràn của một số công trình thủy lợi). Hàm sigmoid có thể là hàm số tăng hoặc giảm, và giá trị trả về thường nằm trong khoảng từ 0 đến 1, mặc dù một phạm vi khác thường gặp là từ −1 đến 1.

Những hàm sigmoid như hàm logistic và hàm hyperbolic đã được áp dụng làm hàm kích hoạt trong các mạng nơ-ron nhân tạo. Đường cong sigmoid cũng rất phổ biến trong thống kê, như các hàm phân phối tích lũy (từ 0 đến 1), bao gồm tích phân của phân phối logistic, phân phối chuẩn, và phân phối t Student.

Định nghĩa

Hàm sigmoid là một hàm số bị giới hạn, khả vi, và định nghĩa cho tất cả các giá trị thực. Nó có một đạo hàm không âm tại mọi điểm và chỉ có duy nhất một điểm uốn, tạo ra hình dạng chữ S. Hàm sigmoid và cường cong sigmoid đều chỉ về cùng một loại hàm số.

Các ví dụ minh họa

• Hàm logistic

$f\left(x\right)=\frac{1}{1+e^{-<!--\; -\; -->x}}$

• Hàm hyperbolic (phiên bản biến thể và thu nhỏ của hàm logistic ở trên)

$f\left(x\right)=\tanh <!--\; \; -->x=\frac{e^x-<!--\; -\; -->e^{-<!--\; -\; -->x}}{e^x+e^{-<!--\; -\; -->x}}$

• Các hàm lượng giác ngược

$f\left(x\right)=\arctan <!--\; \; -->x$

• Hàm Gudermann

$f\left(x\right)=\mathrm{gd}<!--\; \; -->\left(x\right)={\int <!--\; \int \; -->}_0^x\frac{1}{\cosh <!--\; \; -->t}dt=2\arctan <!--\; \; -->\left(\tanh <!--\; \; -->\left(\frac{x}{2}\right)\right)$

• Hàm lỗi

$f\left(x\right)=\mathrm{erf}<!--\; \; -->\left(x\right)=\frac{2}{\sqrt{\mathrm{\pi <!--\; \pi \; -->}}}{\int <!--\; \int \; -->}_0^x{e}^{-<!--\; -\; -->t^2}dt$

• Hàm logistic tổng quát

$f\left(x\right)=(1+e^{-<!--\; -\; -->x}{)}^{-<!--\; -\; -->\mathrm{\alpha <!--\; \alpha \; -->}},\mathrm{\alpha <!--\; \alpha \; -->}>0$

• Hàm smoothstep

• Danh sách một số hàm số đại số, ví dụ

$f\left(x\right)=\frac{x}{\sqrt{1+x^2}}$

• Mitchell, Tom M. (1997). Machine Learning. WCB–McGraw–Hill. ISBN 978-0-07-042807-2.. Đặc biệt xem 'Chương 4: Mạng nơ-ron nhân tạo' (cụ thể trang 96–97) nơi Mitchell dùng từ 'hàm logistic' và 'hàm sigmoid' như nhau – hàm này ông cũng gọi là 'hàm nén' – và hàm sigmoid (hay logistic) được sử dụng để nén các đầu ra của 'nơ-ron' trong các mạng nơ-ron nhiều lớp.
• Humphrys, Mark. “Đầu ra liên tục, hàm sigmoid”. Bản gốc lưu trữ ngày 2 tháng 2 năm 2015. Truy cập ngày 18 tháng 6 năm 2020. Tính chất của hàm sigmoid, bao gồm cách nó có thể dịch chuyển dọc trục và cách miền của nó có thể được biến đổi.