Hằng đẳng thức số 7 - Toán lớp 8 và các bài tập ứng dụng

Buzz

Nội dung bài viết

A. Lý thuyết về 7 hằng đẳng thức

1. Bình phương của tổng

2. Bình phương của một hiệu

3. Hiệu của hai bình phương

4. Khai triển lập phương của một tổng

5. Khai phương của một hiệu

6. Tổng của hai lập phương

7. Hiệu của hai lập phương

8. Phương pháp học hiệu quả 7 hằng đẳng thức quan trọng

B. Ví dụ minh họa về hằng đẳng thức

Xem thêm

Bài viết này từ Mytour trình bày chi tiết về 'Hằng đẳng thức số 7 - Toán lớp 8 và các bài tập ứng dụng', với hy vọng sẽ cung cấp thông tin giá trị cho độc giả.

A. Lý thuyết về 7 hằng đẳng thức

1. Bình phương của tổng

- Bình phương của một tổng được tính bằng cách lấy bình phương số đầu tiên, cộng với hai lần tích của số đầu tiên và số thứ hai, rồi cộng với bình phương số thứ hai.

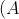
$(A + B)^{2} = A^{2} + 2AB + B^{2}$

Ví dụ như sau:

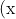
$(mathrm{x}+2)^{2}=mathrm{x}^{2}+2 . mathrm{x} cdot 2+2^{2}=mathrm{x}^{2}+4 mathrm{x}+4$

2. Bình phương của một hiệu

- Bình phương của hiệu giữa hai số được tính bằng cách lấy bình phương số đầu tiên, trừ đi gấp đôi tích của số đầu tiên và số thứ hai, rồi cộng với bình phương của số thứ hai.

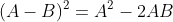
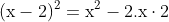
$(A - B)^{2} = A^{2} - 2AB + B^{2}$ $(mathrm{x}-2)^{2}=mathrm{x}^{2}-2 . mathrm{x} cdot 2+2^{2}=mathrm{x}^{2}-4 mathrm{x}+4$

3. Hiệu của hai bình phương

- Hiệu của hai bình phương bằng hiệu của hai số đó nhân với tổng của hai số đó.

$A^{2} - B^{2}$

Ví dụ cụ thể:

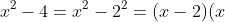
$x^{2}-4=x^{2}-2^{2}=(x-2)(x+2)$

4. Khai triển lập phương của một tổng

- Khai triển lập phương của tổng hai số bằng lập phương của số đầu tiên cộng với ba lần tích của bình phương số đầu tiên và số thứ hai, cộng thêm ba lần tích của số đầu tiên và bình phương số thứ hai, rồi cộng với lập phương của số thứ hai.

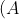
$(A + B)^{3}= A^{3} + 3A^{2}B + 3AB^{2} + B^{3}$

Diễn giải bằng lời: Khai phương của một tổng bằng lập phương số đầu tiên cộng với ba lần tích của bình phương số đầu tiên và số thứ hai, cộng thêm ba lần số đầu tiên nhân với bình phương số thứ hai, rồi cộng với lập phương số thứ hai.

Ví dụ cụ thể

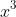
${{left( x+2y ight)}^{3}}={{x}^{3}}+3.{{x}^{2}}.2y+3.x.{{left( 2y ight)}^{2}}+{{left( 2y ight)}^{3}}={{x}^{3}}+6{{x}^{2}}y+12x{{y}^{2}}+8{{y}^{3}}$ ${{left( 1+y ight)}^{3}}={{1}^{3}}+{{3.1}^{2}}.y+3.1.{{y}^{2}}+{{y}^{3}}=1+3y+3{{y}^{2}}+{{y}^{3}}$ ${{x}^{3}}+6{{x}^{2}}+12x+8={{x}^{3}}+3.{{x}^{2}}.2+3.x{{.2}^{2}}+{{2}^{3}}={{left( x+2 ight)}^{3}}$

5. Khai phương của một hiệu

- Khai phương của một hiệu được tính bằng lập phương số đầu tiên trừ ba lần tích của bình phương số đầu tiên và số thứ hai, cộng với ba lần tích số đầu tiên và bình phương số thứ hai, rồi trừ đi lập phương số thứ hai.

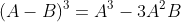
$(A - B)^{3} = A^{3} - 3A^{2}B + 3AB^{2} - B^{3}$

Diễn giải bằng lời: Khai phương của một hiệu bằng lập phương số đầu tiên trừ ba lần tích bình phương số đầu tiên với số thứ hai, cộng với ba lần số đầu tiên nhân bình phương số thứ hai, rồi trừ đi lập phương số thứ hai.

Ví dụ cụ thể

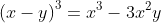
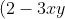
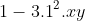
${{\left( x-y \right)}^{3}} = {{x}^{3}} - 3x^{2}y + 3xy^{2} + {{y}^{3}}$ $(2 - 3xy + 3x^{2}y^{2}) - (y^{3}x^{3} + 1) = 2 - 3xy + 3x^{2}y^{2} - x^{3}y^{3} - 1$ $= 1 - 3xy + 3x^{2}y^{2} - x^{3}y^{3}$ $1 - 3.1^{2}xy + 3.1(xy)^{2} - (xy)^{3} = (1 - xy)^{3}$

6. Tổng của hai lập phương

- Tổng hai lập phương bằng tích của tổng hai số với bình phương còn thiếu của hiệu của chúng.

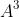
$A^{3} + B^{3} = (A + B)(A^{2} - AB + B^{2})$

Ví dụ:

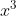
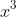
$x^{3} + 8 = x^{3} + 2^{3} = (x + 2)(x^{2} - 2x + 4)$ ${{x}^{3}} + {{y}^{3}} = (x + y)(x^{2} - xy + y^{2})$ ${{\left( 2x-1 \right)}^{3}} = (2x - 1)(4x^{2} + 2x + 1)$

7. Hiệu của hai lập phương

- Hiệu của hai lập phương được tính bằng hiệu hai số nhân với bình phương còn thiếu của tổng hai số.

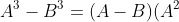
$A^{3} - B^{3} = (A - B)(A^{2} + AB + B^{2})$

Ví dụ:

$\mathrm{du}: \mathrm{x}^{3} - 8 = \mathrm{x}^{3} - 2^{3} = (\mathrm{x} - 2)(\mathrm{x}^{2} + 2\mathrm{x} + 4)$ $\mathrm{x}^{3} - 8 = \mathrm{x}^{3} - 2^{3} = (\mathrm{x} - 2)(\mathrm{x}^{2} + 2\mathrm{x} + 4)$

8. Phương pháp học hiệu quả 7 hằng đẳng thức quan trọng

* Tạo tâm lý tự tin và thoải mái khi học

- Các bạn không nên quá lo lắng mà hãy giữ tinh thần thoải mái để giúp não bộ hoạt động hiệu quả hơn.

- Chuyển từ con số sang lời và tìm hiểu các quy luật trong các công thức tương đồng.

- Nên hiểu bản chất của từng hằng đẳng thức để ghi nhớ công thức lâu dài.

* Luyện tập thường xuyên

Việc luyện tập đều đặn sẽ hình thành phản xạ và thói quen tư duy trong mọi môn học, bao gồm cả việc học 7 hằng đẳng thức này.

- Áp dụng các hằng đẳng thức theo trình tự hợp lý. Bắt đầu bằng cách sử dụng từng loại hằng đẳng thức để giải các bài tập nhỏ, sau đó kết hợp nhiều hằng đẳng thức để giải các bài tập phức tạp hơn khi đã thành thạo.

- Dần dần nâng cao mức độ khó.

- Tránh chủ quan để không rơi vào tình trạng học trước quên sau.

* Ghi nhớ như từ vựng tiếng Anh

Các công thức toán học có thể trở nên nhàm chán, vì vậy cần sử dụng phương pháp sinh động và sáng tạo để khơi gợi sự hứng thú học tập. Một cách hiệu quả là viết các hằng đẳng thức lên các tờ giấy ghi nhớ (Sticker) như cách học từ vựng tiếng Anh. Những tờ giấy màu sắc sẽ thu hút sự chú ý và việc gặp lại nhiều lần sẽ giúp nhớ lâu.

* Học qua bài hát

Có thể bạn sẽ thấy lạ, nhưng hãy thử tìm bài hát về 7 hằng đẳng thức đáng nhớ trên Google và nghe vài lần. Bạn sẽ thấy việc học toán trở nên dễ dàng hơn nhiều.

B. Ví dụ minh họa về hằng đẳng thức

Ví dụ 1

Chuyển các biểu thức sau thành đa thức:

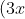
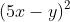
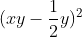
$(3x + 4)^{2}$ $(5x - y)^{2}$ $(xy - \frac{1}{2}y)^{2}$

Gợi ý đáp án

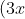
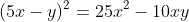
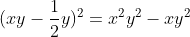
$(3x + 4)^{2} = 9x^{2} + 24x + 16$ $(5x - y)^{2} = 25x^{2} - 10xy + y^{2}$ $(xy - \frac{1}{2}y)^{2} = x^{2}y^{2} - xy^{2} + \frac{1}{4}y^{2}$

Ví dụ 2

Chuyển các biểu thức sau thành bình phương của một tổng hoặc một hiệu

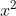
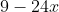
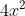
$x^{2} + 2x + 1$ $9 - 24x + 16x^{2}$ $4x^{2} + \frac{1}{4} + 2x$

Gợi ý đáp án

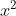
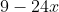
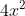
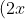
$x^{2} + 2x + 1 = x^{2} + 2x + 1^{2} = (x + 1)^{2}$ $9 - 24x + 16x^{2} = 3^{2} - 24x + (4x)^{2} = (3 - 4x)^{2}$ $4x^{2} + \frac{1}{4} + 2x = (2x)^{2} + 2x + (\frac{1}{2})^{2}$ $(2x + \frac{1}{2})^{2}$

Ví dụ 3

Chuyển các biểu thức sau thành đa thức:

a) (3x - 5)(3x + 5)

b) (x - 2y)(x + 2y)

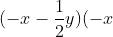
$(-x - \frac{1}{2}y)(-x + \frac{1}{2}y)$

Gợi ý đáp án

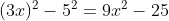
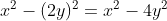
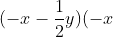
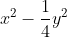
$(3x)^{2} - 5^{2} = 9x^{2} - 25$ $x^{2} - (2y)^{2} = x^{2} - 4y^{2}$ $(-x - \frac{1}{2}y)(-x + \frac{1}{2}y) = (-x)^{2} - (\frac{1}{2}y)^{2}$ $x^{2} - \frac{1}{4}y^{2}$

Ví dụ 4

a) Viết biểu thức diện tích của hình vuông có cạnh là 2x + 3 dưới dạng đa thức

b) Viết biểu thức thể tích của khối lập phương có cạnh là 3x - 2 dưới dạng đa thức

Gợi ý đáp án

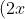
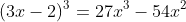
$(2x+3)^{2} = 4x^{2} + 12x + 9$ $(3x-2)^{3} = 27x^{3} - 54x^{2} + 36x - 8$

Ví dụ 5 Tính nhanh

a) 38 x 42

$102^{2}$ $198^{2}$ $75^{2} - 25^{2}$

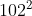
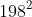
Gợi ý đáp án

a) 38 x 42 = (40-2)(40+2)

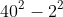
$40^{2} - 2^{2}$ $102^{2} = (100 + 2)^{2} = 100^{2} + 2 imes 100 imes 2 + 2^{2}$

= 10000 + 400 + 4 = 10404

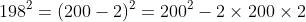
$198^{2} = (200 - 2)^{2} = 200^{2} - 2 imes 200 imes 2 + 2^{2}$

= 40000 - 800 + 4 = 39204

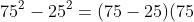
$75^{2} - 25^{2} = (75 - 25)(75 + 25)$

Ví dụ 6

Chuyển đổi các biểu thức dưới đây thành dạng đa thức:

$(2x-3)^{3}$ $(a+3b)^{3}$ $(xy-1)^{3}$

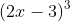
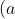
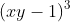
Gợi ý đáp án

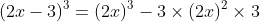
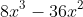
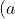
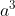
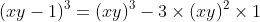
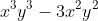
$(2x-3)^{3}=(2x)^{3}-3 imes (2x)^{2} imes 3 + 3 imes 2x imes 3^{2} - 3^{3}$ $8x^{3}-36x^{2}+54x-27$ $(a+3b)^{3}=a^{3}+3 imes a^{2} imes (3b) + 3 imes a imes (3b)^{2} + (3b)^{3}$ $a^{3}+9a^{2}b+27ab^{2}+27b^{3}$ $(xy-1)^{3}=(xy)^{3}-3 imes (xy)^{2} imes 1 + 3 imes xy imes 1^{2} - 1^{3}$ $x^{3}y^{3}-3x^{2}y^{2}+3xy-1$

Ví dụ 7: Rút gọn các biểu thức sau:

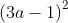
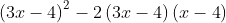
$\left(2a - 3b + 4c\right)\left(2a - 3b - 4c\right)$ $\left(3x + 4y - 5z\right)\left(3x - 4y + 5z\right)$ ${\left(3a - 1\right)^2} + 2 \left(9a^2 - 1\right) + {\left(3a + 1\right)^2}$ ${\left(3x - 4\right)^2} - 2 \left(3x - 4\right) \left(x - 4\right) + {\left(4 - x\right)^2}$

Gợi ý đáp án

$\begin{array}{l} \left(2a - 3b + 4c\right)\left(2a - 3b - 4c\right) \\ = \left(2a - 3b\right)^2 - \left(4c\right)^2 \\ = 4a^2 - 12ab + 9b^2 - 16c^2 \end{array}$

$\begin{array}{l} \left( {3x + 4y - 5z} \right)\left( {3x - 4y + 5z} \right)\\ = {\left( {3x} \right)^2} - {\left( {4y - 5z} \right)^2}\\ = 9{x^2} - \left( {16{y^2} - 40yz + 25{z^2}} \right)\\ = 9{x^2} - 16{y^2} + 40yz - 25{z^2} \end{array}$

$\begin{array}{l} {\left( {3a - 1} \right)^2} + 2\left( {9{a^2} - 1} \right) + {\left( {3a + 1} \right)^2}\\ = {\left( {3a - 1} \right)^2} + 2\left( {3a - 1} \right)\left( {3a + 1} \right) + {\left( {3a + 1} \right)^2}\\ = {\left[ {\left( {3a - 1} \right) + \left( {3a + 1} \right)} \right]^2}\\ = {\left( {6a} \right)^2} = 36{a^2} \end{array}$

$\begin{array}{l} {\left( {3x - 4} \right)^2} - 2\left( {3x - 4} \right)\left( {x - 4} \right) + {\left( {4 - x} \right)^2}\\ = {\left( {3x - 4} \right)^2} - 2\left( {3x - 4} \right)\left( {x - 4} \right) + {\left( {x - 4} \right)^2}\\ = {\left( {3x - 4 - x + 4} \right)^2}\\ = {\left( {2x} \right)^2} = 4{x^2} \end{array}$

Ví dụ 8. Nếu một hình lập phương có cạnh 3 cm, thể tích của nó sẽ thay đổi thế nào nếu mỗi cạnh tăng thêm a cm?

Hướng dẫn giải

Thể tích của hình lập phương ban đầu là

V = 3^3 = 27 (cm³)

Khi mỗi cạnh của hình lập phương được mở rộng thêm a cm, chiều dài các cạnh trở thành 3 + a (cm)

Thể tích của hình lập phương sau khi mở rộng là

V = (3 + a)^3

= (3 + a) cdot (3 + a) cdot (3 + a)

= 27 + 3 cdot 9 cdot a + 3 cdot 3 cdot a^2 + a^3

= a^3 + 9a^2 + 27a + 27 (cm³)

Thể tích hình lập phương sẽ tăng thêm là

a^3 + 9a^2 + 27a + 27 – 27 = a^3 + 9a^2 + 27a (cm³)

Do đó, thể tích của hình lập phương sẽ tăng thêm a^3 + 9a^2 + 27a cm³.

Ví dụ 9. Hiệu của các bình phương của hai số tự nhiên chẵn liên tiếp là 36. Tìm hai số đó.

Giải Đáp

Xét hai số chẵn liên tiếp là x và x + 2 (với x là số chẵn). Ta có:

(x + 2)² – x² = 36

<=> x² + 4x + 4 – x² = 36

<=> 4x = 32

<=> x = 8

<=> số thứ hai là 8 + 2 = 10

Kết quả: 8 và 10

Ví dụ 10: Xác định 3 số nguyên dương liên tiếp sao cho tổng các tích của mọi cặp số trong ba số đó bằng 74

Giải Đáp

Gọi ba số nguyên dương liên tiếp là: x – 1, x, x + 1 (với điều kiện x > 0)

Chúng ta có: x(x – 1) + (x – 1)(x + 1) + x(x + 1) = 74

Tiến hành nhân và đơn giản hóa, ta có:

x² = 25 <=> x = -5 hoặc x = 5

So sánh với điều kiện x > 0, ta chọn x = 5 (kết quả).

Do đó, kết quả là: 4, 5, 6.

Ví dụ 11: Tính nhanh các biểu thức sau:

a) 127² + 146 × 127 + 73²

b) 98 × 28 – (184 – 1)(184 + 1)

c) 100² – 99² + 98² – 97² + … + 2² – 1²

d) (20² + 18² + 16² + … + 4² + 2²) – (19² + 17² + 15² + … + 3² + 1²)

Lời Giải

a) A = 127² + 146 × 127 + 73²

= 127² + 2 × 73 × 127 + 73²

= (127 + 73)²

= 200²

= 40000

b) B = 98 × 28 – (184 – 1)(184 + 1)

= 98 × 28 – (184² – 1)

= 1

c) C = 100² – 99² + 98² – 97² + … + 2² – 1²

= (100 + 99)(100 – 99) + (98 + 97)(98 – 97) + … + (2 + 1)(2 – 1)

= 100 + 99 + 98 + 97 + … + 2 + 1

= 5050

d) D = (20² + 18² + 16² + … + 4² + 2²) – (19² + 17² + 15² + … + 3² + 1²)

= (20² – 19²) + (18² – 17²) + (16² – 15²) + … + (4² – 3²) + (2² – 1²)

= (20 + 19)(20 – 19) + (18 + 17)(18 – 17) + (16 + 15)(16 – 15) + … + (4 + 3)(4 – 3) + (2 + 1)(2 – 1)

= 20 + 19 + 18 + 17 + 16 + 15 + … + 4 + 3 + 2 + 1

= 210

Ví dụ 12: Tính giá trị biểu thức A =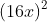

- 24x + 9 khi x = 1

Gợi ý đáp án

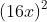
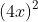
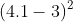
Khi thay x = 1 vào biểu thức (*) ta có:

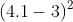
Vì vậy, khi x = 1, giá trị của biểu thức A là 1

Nội dung được phát triển bởi đội ngũ Mytour với mục đích chăm sóc khách hàng và chỉ dành cho khích lệ tinh thần trải nghiệm du lịch, chúng tôi không chịu trách nhiệm và không đưa ra lời khuyên cho mục đích khác.

Nếu bạn thấy bài viết này không phù hợp hoặc sai sót xin vui lòng liên hệ với chúng tôi qua email [email protected]