1. Kiến thức cơ bản về hình Oxyz
Trong hệ trục không gian, chúng ta xem xét ba trục tọa độ Ox, Oy, Oz, vuông góc với nhau tại điểm gốc O. Các tia i, j, k là các vectơ đơn vị tương ứng với các trục Ox, Oy, Oz. Hệ ba trục này được gọi là hệ trục tọa độ vuông góc trong không gian.
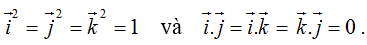
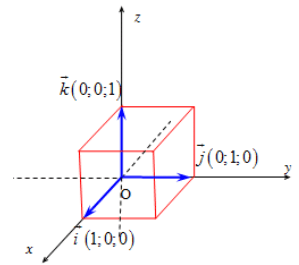
2. Các công thức của hình Oxyz trong không gian
- Cho điểm A (xA; yA; zA) và điểm B (xB; yB; zB)
tia AB = (xB - xA; yB - yA; zB - zA)
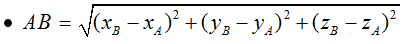
Tọa độ của điểm giữa đoạn thẳng AB: M (xA + xB)/2; (yA + yB)/2; (zA + zB)/2)
Tọa độ của trọng tâm G trong tam giác ABC: G ((xA + xB + xC)/3; (yA + yB + yC)/3; (zA + zB + zC)/3)
Tọa độ của trọng tâm G trong tứ diện ABCD: G ((xA + xB + xC + xD)/4; (yA + yB + yC + yD)/4; (zA + zB + zC + zD)/4)
- Tích có hướng giữa hai vectơ
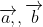
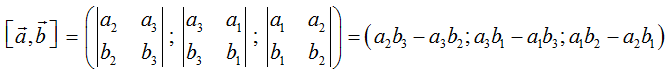
Lưu ý: Tích có hướng của hai vectơ tạo thành một vectơ mới, trong khi tích vô hướng là một giá trị số.
b. Đặc điểm:
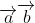
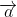
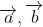
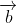
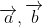
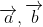
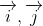
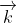
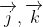
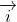
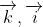
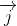
![| [→ a] → b |](https://img.tripi.vn/cdn-cgi/image/width=700,height=700/https://gcs.tripi.vn/public-tripi/tripi-feed/img/479268fNp/anh-mo-ta.png)
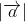

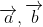
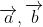
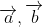
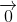
Lưu ý:
- Tích vô hướng của hai vectơ thường dùng để chứng minh hai đường thẳng vuông góc hoặc tính góc giữa chúng.
- Tích có hướng của hai vectơ thường dùng để tính diện tích tam giác, thể tích khối tứ diện, xác định hình hộp, chứng minh các vectơ đồng phẳng hoặc không đồng phẳng, và cùng phương.

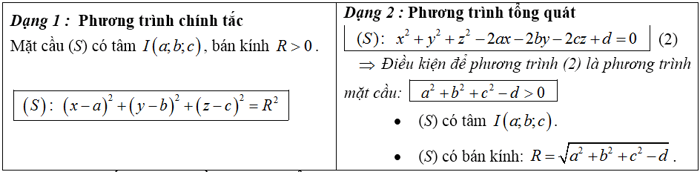
Phương trình của mặt cầu:
a. định nghĩa:
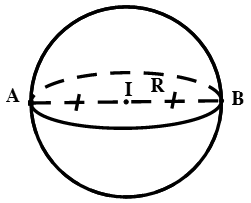
Nếu I là một điểm cố định và R là một số thực dương, thì tập hợp tất cả các điểm M trong không gian cách I một khoảng R được gọi là mặt cầu có tâm I và bán kính R.
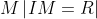
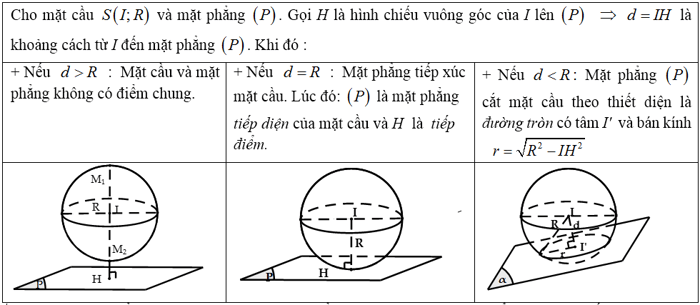
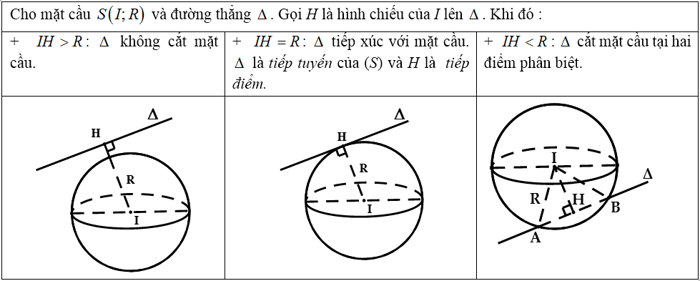
c. Mối quan hệ giữa mặt cầu và đường thẳng:
3. Bài tập ứng dụng liên quan đến hệ tọa độ Oxyz
1. Xác định phương trình của mặt cầu (S) trong các trường hợp sau:
a. (S) có tâm I (2; 2; -3) và bán kính R = 3
b. (S) có tâm I (1; 2; 0) và mặt cầu (S) đi qua điểm P (2; -2; 1)
c. (S) có đường kính AB với các điểm A (1; 3; 1) và B (-2; 0; 1).
2. Xác định phương trình của mặt cầu (S) trong các tình huống sau:
a. (S) đi qua các điểm A (3; 1; 0), B (5; 5; 0), với tâm I nằm trên trục Ox
b. (S) có tâm tại gốc tọa độ O và tiếp xúc với mặt phẳng (a): 16x - 15y - 12z + 75 = 0
c. (S) có tâm I (-1; 2; 0) và tiếp tuyến của nó là một đường thẳng.
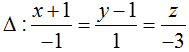
3. Trong hệ tọa độ Oxy, xem xét hình hộp chữ nhật ABCD với các đỉnh A', B', C', D'. Đỉnh A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), và A' (0; 0; n) với m, n > 0 và tổng m + n = 4. Gọi M là trung điểm của cạnh CC'. Tính thể tích của tứ diện BDA'M khi giá trị đạt cực đại.
A. 245/108
B. 9/4
C. 64/27
D. 75/32
4. Trong không gian, xét tam giác đều ABC với cạnh bằng 2. Điểm M thỏa mãn điều kiện MA² + MB² + MC² = 12. Định lý nào dưới đây là đúng?
5. Trong không gian Oxyz, phương trình của mặt phẳng đi qua ba điểm
(0; -1; 2), B(-2; 0; 3) và C(1; 2; 0) là:
A. 7x - 5y - 3z + 1 = 0
B. 7x - 5y - 3z + 11 = 0
C. 5x + 3y + 7z - 17 = 0
D. 5x + 3y + 7z - 11 = 0
6. Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD. A'B'C'D' có điểm A trùng với gốc tọa độ, B (a; 0; 0), D (0; a; 0), A' (0; 0; b) với a > 0, b > 0. Gọi M là trung điểm của cạnh CC'. Giả sử a + b = 4, giá trị lớn nhất của thể tích khối tứ diện A'BDM là:
A. 64/27
B. 128/27
C. 128/9
D. 27/4
7. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (0; 0; 0), B (0; 1; 1), C (1; 0; 1). Xét điểm D nằm trên mặt phẳng Oxy sao cho tứ diện ABCD trở thành một tứ diện đều. Gọi D(x0; y0; z0) là tọa độ của điểm D. Tổng của x0 + y0 là:
A. 0
B. 1
C. 2
D. 3
8. Tìm phương trình của mặt phẳng đi qua điểm A(1; 1; 1) và vuông góc với hai mặt phẳng (a): x + y - z - 2 = 0, (b): x - y + z = 0
A. y + z - 2 = 0
B. x + y + z - 3 = 0
C. x - 2y + z = 0
D. x + z - 2 = 0
9. Trong không gian với hệ tọa độ Oxyz, xác định phương trình mặt phẳng đi qua điểm M (1; -2; 3) và vuông góc với hai mặt phẳng (P): 2x - y - z - 1 = 0; (Q): x - y + z - 3 = 0
A. 2x + 3y + z - 1 = 0
B. x + 3y + 2z - 1 = 0
C. 2x + 3y + z + 1 = 0
10. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (0; 8; 0), B (-4; 6; 2) và C (0; 12; 4). Tìm phương trình mặt cầu đi qua ba điểm A, B, C và có tâm nằm trên mặt phẳng (Oyz).
11. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x + 1/2 = y/-1 = z - 1/1 và điểm A (0; -1; 3). Xác định phương trình mặt phẳng (P) đi qua điểm A và chứa đường thẳng d.
A. (P): x + 3y + z = 0
B. (P): x + 4y + 2z - 2 = 0
C. (P): 2x + 3y - z + 6 = 0
D. (P): x + 3y + z - 6 = 0
12. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) có phương trình 2x - 2y - 3z = 0. Tìm phương trình của mặt phẳng (Q) đi qua hai điểm H (1; 0; 0) và K (0; -2; 0), biết rằng (Q) vuông góc với (P).
A. (Q): 6x + 3y + 4z + 6 = 0
B. (Q): 2x - y + 2z - 2 = 0
C. (Q): 2x - y + 2z + 2 = 0
D. (Q): 2x + y + 2z - 2 = 0
13. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P): ax + by + cz - 27 = 0 đi qua hai điểm A (3; 2; 1), B (-3; 5; 2) và vuông góc với mặt phẳng (Q): 3x + y + z + 4 = 0. Tính tổng S = a + b + c.
14. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3/2 = y - 1/3 = z + 1/-1 và điểm A (1; 3; -1). Xác định phương trình mặt phẳng (P) chứa d và đi qua A.
A. 2x - y + z - 4 = 0
B. x + y + 5z + 1 = 0
C. x + y - 4 = 0
D. x - y - z + 1 = 0
15. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) với phương trình x² + y² + z² - 2x + 4y - 6z - 11 = 0 và mặt phẳng (P) với phương trình 2x + 2y - z + 17 = 0. Xác định phương trình của mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) tạo thành giao tuyến là một đường tròn có chu vi bằng 6π.
