Hiểu Mô hình Giá Tùy chọn Nhị phân

Xác định Giá Cổ phiếu

Để đồng ý về việc xác định giá chính xác cho bất kỳ tài sản có thể giao dịch nào cũng là một thách thức—đó là lý do tại sao giá cổ phiếu thay đổi liên tục. Trong thực tế, các công ty hiếm khi thay đổi định giá của họ hàng ngày, nhưng giá cổ phiếu và định giá của họ thay đổi gần như mỗi giây. Sự khó khăn này trong việc đạt được một thỏa thuận về giá đúng cho bất kỳ tài sản có thể giao dịch nào dẫn đến các cơ hội giao dịch bất công ngắn hạn.

Nhưng nhiều thành công trong đầu tư dừng lại ở một câu hỏi đơn giản về định giá ngày nay– giá hiện tại đúng là bao nhiêu hôm nay cho một lợi ích tương lai dự kiến?

Nhận Điều Cần Lưu Ý

Định Giá Tùy chọn Nhị phân

Trong một thị trường cạnh tranh, để tránh các cơ hội giao dịch bất công, các tài sản có cùng cấu trúc thanh toán phải có cùng giá. Việc định giá các tùy chọn đã là một nhiệm vụ khó khăn và biến đổi giá dẫn đến các cơ hội giao dịch bất công. Black-Scholes vẫn là một trong những mô hình phổ biến nhất được sử dụng để định giá tùy chọn nhưng có những hạn chế.

Mô hình giá tùy chọn nhị phân là một phương pháp phổ biến khác được sử dụng để định giá các tùy chọn.

Ví dụ

Giả sử có một tùy chọn mua trên một cổ phiếu cụ thể với giá thị trường hiện tại là $100. Tùy chọn gần giá (ATM) có giá thực hiện là $100 với thời gian đến hạn trong một năm. Có hai nhà giao dịch, Peter và Paula, cả hai đều đồng ý rằng giá cổ phiếu sẽ tăng lên $110 hoặc giảm xuống $90 trong một năm.

Họ đồng ý về các mức giá dự kiến trong một khoảng thời gian nhất định là một năm nhưng không đồng ý về xác suất của di chuyển lên hoặc xuống. Peter tin rằng xác suất giá cổ phiếu tăng lên $110 là 60%, trong khi Paula tin rằng nó là 40%.

Dựa trên đó, ai sẵn lòng trả giá cao hơn cho tùy chọn mua? Có thể là Peter, vì anh ấy dự kiến có xác suất cao của sự di chuyển lên.

Tính Toán Tùy chọn Nhị phân

Hai tài sản, mà định giá phụ thuộc vào đó, là tùy chọn mua và cổ phiếu cơ bản. Có sự đồng ý giữa các bên tham gia rằng giá cổ phiếu cơ bản có thể di chuyển từ mức $100 hiện tại lên $110 hoặc xuống $90 trong một năm và không có các di chuyển giá khác có thể xảy ra.

Trong một thế giới không có cơ hội lợi nhuận, nếu bạn muốn tạo ra một danh mục gồm hai tài sản này, là tùy chọn gọi và cổ phiếu cơ sở, sao cho bất kể giá cơ sở đi đến đâu – $110 hoặc $90 – lợi nhuận ròng trên danh mục luôn giữ nguyên. Giả sử bạn mua 'd' cổ phiếu cơ sở và bán ngắn một tùy chọn gọi để tạo ra danh mục này.

Nếu giá tăng lên $110, cổ phiếu của bạn sẽ có giá trị là $110*d, và bạn sẽ mất $10 trên phần trả lại của tùy chọn gọi. Giá trị ròng của danh mục của bạn sẽ là (110d - 10).

Nếu giá giảm xuống $90, cổ phiếu của bạn sẽ có giá trị là $90*d, và tùy chọn sẽ hết hạn không có giá trị. Giá trị ròng của danh mục của bạn sẽ là (90d).

Nếu bạn muốn giá trị danh mục của mình luôn giữ nguyên bất kể giá cổ phiếu cơ sở đi đến đâu, thì giá trị danh mục của bạn nên giữ nguyên trong cả hai trường hợp:

h(d) - m = l(d), trong đó:

Nếu bạn mua một nửa cổ phiếu, giả sử mua các phần mảnh nhỏ được cho phép, bạn sẽ tạo ra một danh mục để giá trị của nó luôn giữ nguyên trong cả hai trạng thái có thể có trong khung thời gian một năm được chỉ định.

Danh mục này, được chỉ ra bởi (90d) hoặc (110d - 10) = 45, là một năm sau. Để tính toán giá trị hiện tại của nó, nó có thể được chiết khấu bằng tỷ lệ lợi nhuận không rủi ro (giả sử 5%).

Giá trị hiện tại = 90d × e^ { (-5% × 1 Năm) } = 45 × 0.9523 = 42.85

Vì hiện tại, danh mục này bao gồm ½ cổ phiếu của cơ sở (với giá thị trường là $100) và một tùy chọn gọi ngắn, nên nó phải bằng giá trị hiện tại.

Since at present, the portfolio is comprised of ½ share of underlying stock (with a market price of $100) and one short call, it should be equal to the present value.

\(\frac { 1 }{ 2} \times 100 - 1 \times \text{Giá gọi} = \$42.85\)

Vì giả định rằng giá trị danh mục không thay đổi bất kể giá cơ bản đi theo hướng nào, nên xác suất tăng giảm không có bất kỳ vai trò nào. Danh mục vẫn là không rủi ro bất kể giá cơ bản di chuyển như thế nào.

Trong cả hai trường hợp (giả định tăng lên $110 và giảm xuống $90), danh mục của bạn là trung lập với rủi ro và thu được tỷ lệ lợi nhuận không rủi ro.

Do đó cả hai nhà giao dịch, Peter và Paula, đều sẵn lòng trả cùng $7.14 cho tùy chọn gọi này, mặc dù họ có nhận thức khác nhau về xác suất tăng (60% và 40%). Xác suất cá nhân của họ không quan trọng trong định giá tùy chọn.

Giả sử thay vì đó là các xác suất cá nhân quan trọng, cơ hội lợi nhuận có thể đã xuất hiện. Trong thế giới thực, các cơ hội lợi nhuận như vậy tồn tại với sự chênh lệch giá nhỏ và biến mất trong thời gian ngắn.

Nhưng điều quan trọng và nhạy cảm nhất ảnh hưởng đến việc định giá tùy chọn là đâu? Biến động giá đã được tính vào tự nhiên của định nghĩa vấn đề. Giả sử hai trạng thái (và chỉ hai — do đó là tên “nhị phân”) của mức giá ($110 và $90), biến động được ngụ ý trong giả định này và tự động bao gồm (10% mỗi cách trong ví dụ này).

Biến động đã được bao gồm trong định nghĩa vấn đề. Giả định về hai (và chỉ hai — do đó là tên “nhị phân”) trạng thái của mức giá ($110 và $90), biến động được ngụ ý trong giả định này và tự động bao gồm (10% mỗi cách trong ví dụ này).

Black-Scholes

Nhưng phương pháp này có chính xác và nhất quán với giá định Black-Scholes thường được sử dụng không? Kết quả máy tính tùy chọn (được tài trợ bởi OIC) khá khớp với giá trị tính toán:

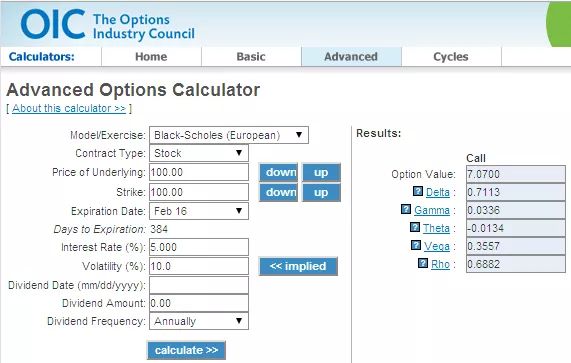
Thật không may, thế giới thực không đơn giản như “chỉ có hai trạng thái.” Cổ phiếu có thể đạt được nhiều mức giá trước thời hạn hết hạn.

Có thể bao gồm tất cả các cấp độ đa dạng này trong một mô hình định giá nhị phân chỉ giới hạn trong hai cấp độ không? Có, hoàn toàn có thể, nhưng để hiểu điều đó cần một vài phép toán đơn giản.

Toàn bộ mô hình định giá nhị phân này có thể bao gồm tất cả các cấp độ đa dạng này không? Có, hoàn toàn có thể, nhưng để hiểu điều đó cần một vài phép toán đơn giản.

Để tổng quát hóa vấn đề và giải pháp:

'X' là giá thị trường hiện tại của một cổ phiếu và 'X*u' và 'X*d' là giá trị tương lai cho các bước tăng và giảm 't' năm sau. Hệ số 'u' sẽ lớn hơn một vì nó chỉ ra một bước tăng và 'd' sẽ nằm giữa không và một. Đối với ví dụ trên, u = 1.1 và d = 0.9.

Các khoản thanh toán tùy chọn mua là 'P_up' và 'P_dn' cho các bước tăng và giảm tại thời điểm hết hạn.

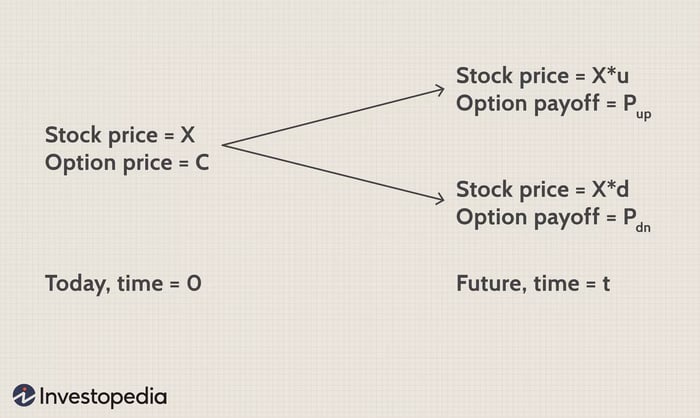
Nếu bạn xây dựng một danh mục đầu tư gồm 's' cổ phiếu mua vào hôm nay và viết ngắn một tùy chọn mua, sau thời gian 't':

Khi bước tăng giá, 'VUM' = s × X × u - P_up

Khi bước giảm giá, 'VDM' = s × X × d - P_down

Đối với định giá tương tự trong cả hai trường hợp của di chuyển giá:

Khi bước tăng giá, 's × X × u - P_up = s × X × d - P_down'

's = (P_up - P_down) / (X × (u - d))' là số cổ phiếu cần mua cho

Giá trị tương lai của danh mục đầu tư vào cuối 't' năm sẽ là:

Khi bước tăng giá, 's × X × u - P_up = (P_up - P_down) / (u - d) × u - P_up'

Trong trường hợp giảm giá, giá trị hiện tại có thể được tính bằng cách giảm giá với tỷ lệ lợi nhuận không rủi ro:

Giá trị hiện tại có thể được tính bằng cách giảm giá với tỷ lệ lợi nhuận không rủi ro:

Giá trị hiện tại có thể được tính bằng cách giảm giá với tỷ lệ lợi nhuận không rủi ro:

Giá trị hiện tại có thể được tính bằng cách giảm giá với tỷ lệ lợi nhuận không rủi ro:

Lưu ý: Nếu phí gọi có ngắn hạn, nó nên được thêm vào danh mục, không phải là một phép trừ.

Biểu diễn phương trình dưới dạng khác bằng cách sắp xếp lại:

Đặt 'q' là:

Cách khác để viết phương trình là sắp xếp lại nó:

Lấy 'q' làm:

Khi đó, phương trình trở thành:

Dịch lại phương trình thành về “q” đã mở ra một góc nhìn mới.

Bây giờ bạn có thể hiểu “q” là xác suất của động thái tăng của cơ sở (vì “q” liên quan đến P_up và “1-q” liên quan đến P_down). Nhìn chung, phương trình biểu diễn giá tùy chọn ngày hôm nay, giá trị chiết khấu của lợi nhuận tại thời hạn đáo hạn của nó.

“Q” này Khác Biệt

Làm thế nào xác suất “q” này khác biệt so với xác suất của một động thái tăng hoặc một động thái giảm của cơ sở?

Giải thích về cách “q” khác biệt so với xác suất của một động thái tăng hoặc giảm của cơ sở?

Thay thế giá trị của “q” và sắp xếp lại, giá cổ phiếu tại thời điểm “t” là:

Trong thế giới giả định này của hai trạng thái, giá cổ phiếu tăng đơn giản bằng tỷ lệ lợi nhuận không rủi ro, chính xác như một tài sản không rủi ro, và do đó nó không phụ thuộc vào bất kỳ rủi ro nào. Nhà đầu tư làm thế nào tới rủi ro trong mô hình này, vì vậy điều này tạo thành mô hình trung lập rủi ro.

Xác suất “q” và '(1-q)' được biết đến là xác suất trung lập rủi ro và phương pháp định giá được biết đến là mô hình định giá trung lập rủi ro.

Thay thế giá trị của “q” và sắp xếp lại, giá cổ phiếu tại thời điểm “t” là:

Xác suất “q” và '(1-q)' được biết đến là xác suất trung lập rủi ro và phương pháp định giá được biết đến là mô hình định giá trung lập rủi ro.

Tình huống ví dụ có một yêu cầu quan trọng – cấu trúc thanh toán tương lai cần được xác định chính xác (mức $110 và $90). Trong thực tế, việc có được sự rõ ràng về các mức giá dựa trên bước di chuyển không khả thi; thay vào đó, giá di chuyển ngẫu nhiên và có thể định cư ở nhiều mức khác nhau.

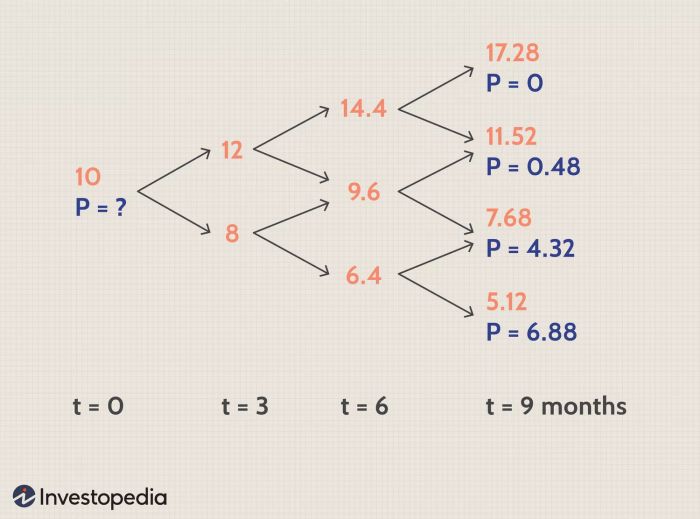
Để mở rộng ví dụ, giả định rằng có thể có hai mức giá dựa trên bước. Chúng ta biết được các thanh toán cuối cùng của bước thứ hai và chúng ta cần định giá tùy chọn ngày hôm nay (tại bước ban đầu):

Làm ngược lại, định giá bước trung gian đầu tiên (tại t = 1) có thể được thực hiện bằng cách sử dụng các thanh toán cuối cùng tại bước hai (t = 2), sau đó sử dụng các định giá bước đầu tiên này (t = 1) đã tính được, định giá ngày hôm nay (t = 0) có thể được đạt được với các tính toán này.

Để có giá lựa chọn ở số hai, ta sử dụng payoffs ở bốn và năm. Để có giá ở số ba, ta sử dụng payoffs ở năm và sáu. Cuối cùng, sử dụng payoffs tính toán ở hai và ba để có giá ở số một.

Vui lòng lưu ý rằng ví dụ này giả định cùng một yếu tố cho các bước lên (và xuống) tại cả hai bước – u và d được áp dụng một cách kết hợp.

Một Ví dụ Thực Tế

Giả sử một lựa chọn bán với giá chấm dứt là $110 hiện đang giao dịch ở $100 và hết hạn trong một năm. Tỷ lệ không rủi ro hàng năm là 5%. Dự kiến giá tăng 20% và giảm 15% mỗi sáu tháng.

Ở đây, u = 1.2 và d = 0.85, x = 100, t = 0.5

Sử dụng công thức đã suy diễn ở trên

Ta có q = 0.35802832

Giá của lựa chọn bán tại điểm 2,

Ở đây, q = 0.35802832

Ta có p_2 = e (-rt) × (p × P_upup + ( 1 - q) P_updn )

Tại điều kiện P_upup, giá cơ sở sẽ là 100*1.2*1.2 = $144 dẫn đến P_upup = zero

Tại điều kiện P_updn, giá cơ sở sẽ là 100*1.2*0.85 = $102 dẫn đến P_updn = $8

Tại điều kiện P_dndn, giá cơ sở sẽ là 100*0.85*0.85 = $72.25 dẫn đến P_dndn = $37.75

p₂ = 0.975309912*(0.35802832*0+(1-0.35802832)*8) = 5.008970741

Tương tự, p₃ = 0.975309912*(0.35802832*8+(1-0.35802832)*37.75) = 26.42958924

$p_1=e(-rt)\times (q\times p_2+(1-q\left)p_3\right)$p1​=e(−rt)×(q×p2​+(1−q)p3​)

Do đó, giá của lựa chọn bán, p₁ = 0.975309912*(0.35802832*5.008970741+(1-0.35802832)* 26.42958924) = $18.29.

Tương tự, các mô hình nhị phân cho phép bạn chia nhỏ thời gian của toàn bộ lựa chọn thành nhiều bước và mức độ tinh tế hơn. Sử dụng các chương trình máy tính hoặc bảng tính, bạn có thể làm ngược lại một bước một lần để có được giá trị hiện tại của lựa chọn mong muốn.

Một Ví Dụ Khác

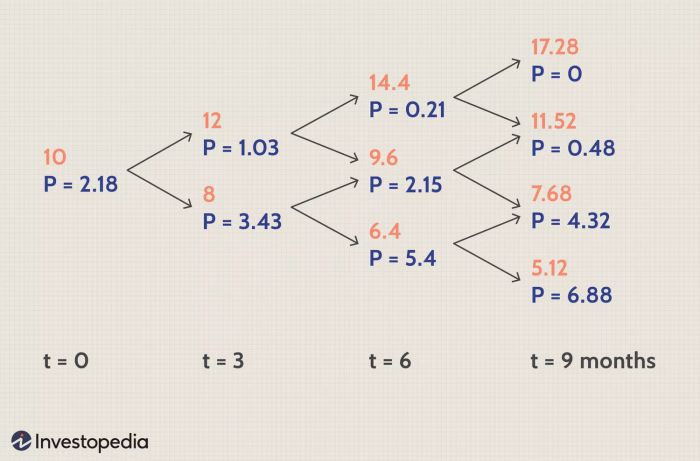
Giả sử một lựa chọn bán kiểu châu Âu với thời gian đáo hạn là chín tháng, giá chấm dứt là $12 và giá cơ sở hiện tại là $10. Giả sử tỷ lệ không rủi ro là 5% cho tất cả các khoảng thời gian. Giả sử mỗi ba tháng, giá cơ sở có thể tăng 20% hoặc giảm 20%, cho chúng ta u = 1.2, d = 0.8, t = 0.25 và một cây nhị phân ba bước.

Màu đỏ biểu thị giá cơ sở, trong khi màu xanh biểu thị phần thưởng của lựa chọn bán. 

Xác suất không rủi ro 'q' tính được là 0.531446.

Sử dụng giá trị 'q' ở trên và giá trị phần thưởng tại t = chín tháng, các giá trị tương ứng tại t = sáu tháng được tính như sau:

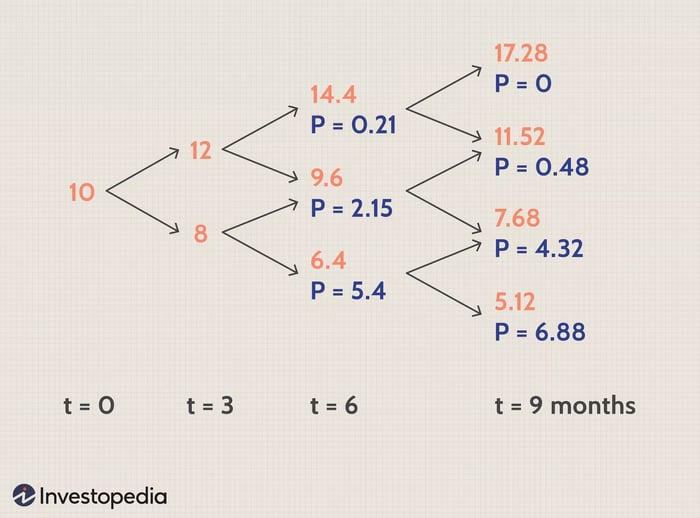
Tiếp theo, sử dụng những giá trị tính được này tại t = 6, các giá trị tại t = 3 sau đó tại t = 0 là:

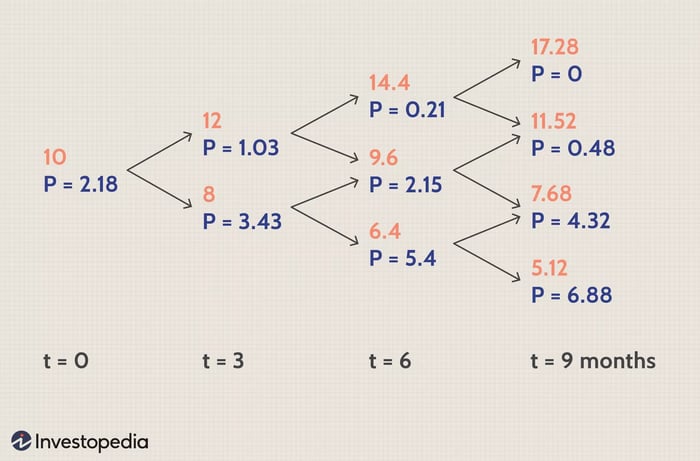
Điều đó cho giá trị hiện tại của một lựa chọn bán là $2.18, khá gần với những gì bạn sẽ tìm thấy khi thực hiện các tính toán bằng mô hình Black-Scholes ($2.30).

Kết luận

Mặc dù sử dụng các chương trình máy tính có thể làm cho những tính toán phức tạp này trở nên dễ dàng, việc dự đoán giá cả trong tương lai vẫn là một hạn chế lớn của các mô hình nhị phân cho việc định giá lựa chọn. Càng tinh tế các khoảng thời gian, càng khó để dự đoán phần thưởng vào cuối mỗi kỳ với độ chính xác cao.

Tuy nhiên, tính linh hoạt trong việc tích hợp những thay đổi dự kiến ​​tại các giai đoạn khác nhau là một điểm cộng, làm cho nó phù hợp cho việc định giá các lựa chọn Mỹ, bao gồm đánh giá trước thời hạn.

Các giá trị tính toán bằng mô hình nhị phân gần giống những giá trị tính toán từ các mô hình phổ biến khác như Black-Scholes, điều này cho thấy tính tiện ích và độ chính xác của các mô hình nhị phân cho việc định giá lựa chọn. Các mô hình định giá nhị phân có thể được phát triển theo ý thích của một nhà giao dịch và có thể hoạt động như một phương án thay thế cho Black-Scholes.