Hình chiếu là một trong những kiến thức trọng tâm mà các em sẽ học trong chương trình Toán 7 và Toán 8. Hình chiếu là khái niệm đo lường khoảng cách vuông góc từ một điểm đến một đường thẳng hoặc một mặt phẳng. Khi tìm hình chiếu, nó giúp chúng ta biết được vị trí của một điểm trên không gian.
Hình chiếu là một khái niệm quan trọng trong toán học vì nó giúp chúng ta hiểu và đặc trưng hóa các khía cạnh không gian của các vật thể. Vậy cách vẽ hình chiếu như thế nào? Có mấy loại phép chiếu? Mời các bạn cùng chúng tôi theo dõi bài học hôm nay nhé. Ngoài ra, các bạn có thể xem thêm các trường hợp bằng nhau của tam giác vuông.
1. Hình chiếu là gì?
Hình chiếu trong Toán học là khoảng cách giữa 2 điểm của đoạn thẳng đó kẻ từ 2 điểm của đoạn thẳng đó vuông góc với đường thẳng cho trước.
Còn hình chiếu của một điểm là điểm mà đường thẳng cho trước và đường thẳng kẻ từ điểm đó vuông góc với đường thẳng đã cho giao nhau.
2. Cách vẽ hình chiếu trong Toán học
Cách vẽ hình chiếu trong Toán học đơn giản hơn trong Kỹ thuật. Đây là phép tính cơ bản, không cần phải tưởng tượng quá nhiều.
Có 3 loại phép chiếu là:
- Phép chiếu xuyên tâm: Các tia chiếu bắt nguồn từ một điểm (tâm chiếu).
- Phép chiếu song song: Các tia chiếu chạy song song với nhau.
- Phép chiếu vuông góc: Các tia chiếu tạo thành góc vuông với mặt phẳng chiếu.
Từ mỗi phép chiếu khác nhau sẽ tạo ra các hình chiếu khác nhau. Trong bài viết này, chúng tôi tập trung vào việc trình bày cụ thể về hình chiếu vuông góc vì đây là phương pháp thường được sử dụng phổ biến nhất.
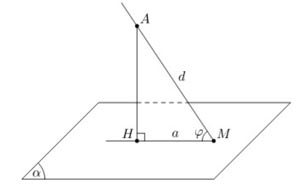
* Hình chiếu vuông góc là gì?
Hình chiếu vuông góc trên một mặt phẳng là hình chiếu trùng với mặt phẳng với một góc 90 độ.
Ví dụ, nếu điểm H nằm trên đường thẳng AH và vuông góc với mặt phẳng (Q) tại H, thì H được gọi là hình chiếu vuông góc của điểm A lên mặt phẳng (Q).
Các dạng hình chiếu vuông góc bao gồm:
- Hình chiếu đứng nhìn từ mặt trước của mặt phẳng
- Hình chiếu cạnh nhìn từ bên trái hoặc bên phải của vật thể
- Hình chiếu bằng nhìn từ trên xuống vật thể.
3. Các tính chất quan trọng của hình chiếu
Các tính chất quan trọng của hình chiếu trong toán 8 bao gồm:
1. Vị trí: Hình chiếu của một điểm nằm trên đường thẳng đã cho. Nếu điểm đó nằm trên đường thẳng, thì hình chiếu sẽ trùng với điểm đó.
2. Đồng thời: Hình chiếu của hai điểm gần nhau trên đường thẳng sẽ gần nhau và nằm trên cùng một phía so với đường thẳng.
3. Nằm trong: Hình chiếu của một điểm trên đoạn thẳng có thể nằm bên trong hoặc nằm trên phần kéo dài của đoạn thẳng tùy thuộc vào vị trí của điểm.
4. Khoảng cách: Khoảng cách giữa hai điểm cũng tương đương với khoảng cách giữa các hình chiếu của chúng trên đường thẳng.
5. Vuông góc: Hình chiếu của một điểm trên một đoạn thẳng vuông góc với đường thẳng đã cho.
Đây là một số tính chất quan trọng của hình chiếu trong toán 8. Hiểu và áp dụng các tính chất này sẽ giúp chúng ta giải quyết các bài toán liên quan đến hình chiếu một cách chính xác và hiệu quả.
4. Các loại phép chiếu thường gặp
Có 3 loại phép chiếu là:
- Hình chiếu thẳng góc là phương pháp đơn giản, giữ nguyên hình dạng và kích thước của vật thể.
- Hình chiếu thẳng góc chỉ hiển thị 2 chiều nên cần nhiều hình chiếu để mô tả, đặc biệt đối với những vật thể phức tạp. Thường sử dụng 3 hình chiếu phổ biến là hình chiếu đứng, hình chiếu cạnh và hình chiếu bằng.
- Hình chiếu trục đo thể hiện 3 chiều của vật thể lên mặt phẳng chiếu, với các tia chiếu song song tùy theo hướng chiếu.
- Hình chiếu trục đo có thể hiển thị toàn bộ ba chiều của vật thể lên mặt phẳng chiếu. Các tia chiếu song song với nhau, có thể vuông góc hoặc góc xiên tùy thuộc vào hướng chiếu. Hình chiếu trục đo được chia thành hai loại là hình chiếu trụ đo vuông góc và hình chiếu trục đo xiên góc, cùng với hình chiếu phối cảnh. Cụ thể các loại hình chiếu này là:
- Hình chiếu trục đo vuông góc: có ba hệ số biến dạng đều nhau trên ba trục; hai trong ba hệ số biến dạng cân bằng nhau; ba hệ số biến dạng lệch với nhau.
- Hình chiếu trục đo xiên góc: biến dạng đều trên các trục; cân bằng đều trên các trục; lệch đều trên các trục.
- Hình chiếu phối cảnh sử dụng phép chiếu xuyên tâm, các tia chiếu hội tụ tại một điểm gọi là điểm tụ. Số lượng điểm tụ xác định loại hình chiếu phối cảnh, bao gồm 1 điểm tụ, 2 điểm tụ và 3 điểm tụ.
- Hình chiếu phối cảnh Curvilinnear perspective sử dụng một khung cơ sở là một mạng đường cong để hiển thị hưởng nhìn từ trên xuống và hướng nhìn từ dưới lên. Hình chiếu phối cảnh rút gọn khoảng cách foresshoting để tạo cảm giác khoảng cách gần hơn với người xem.
Trong hình chiếu trục đo còn nhiều loại khác như hình chiếu trục đo vuông góc và hình chiếu trục đo xiên góc.
5. Có bao nhiêu loại phép chiếu?
Một số loại phép chiếu thường gặp trong toán học là:
- Phép chiếu vuông góc sử dụng các tia chiếu vuông góc với mặt phẳng chiếu.
- Phép chiếu song song sử dụng các tia chiếu chạy song song với nhau.
- Phép chiếu xuyên tâm sử dụng các tia chiếu hội tụ tại một điểm.
6. Hình chiếu vuông góc là gì?
Hình chiếu vuông góc trên một mặt phẳng là hình chiếu mà góc giữa đường chiếu và mặt phẳng là 90 độ.
Nếu điểm H là hình chiếu vuông góc của điểm A lên mặt phẳng (Q) khi AH vuông góc với mặt phẳng (Q) tại H.
Các loại hình chiếu vuông góc bao gồm:
- Hình chiếu đứng nhìn từ phía trước của mặt phẳng
- Hình chiếu cạnh nhìn từ phía trái hoặc phải của vật thể
- Hình chiếu bằng nhìn từ trên cao xuống vật thể.
7. Liên hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Cho điểm A nằm ngoài đường thẳng d, kẻ một đường thẳng vuông góc với đường thẳng d tại H trên d, chọn điểm B không trùng với H. Khi đó:
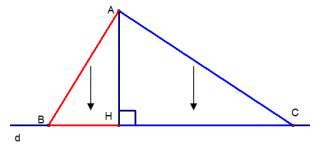
- Đoạn thẳng AH được gọi là đoạn vuông góc hoặc đường vuông góc kẻ từ điểm A đến đường thẳng d.
- Điểm H là chân của đường vuông góc hoặc là hình chiếu của điểm A lên đường thẳng d.
- Đoạn thẳng AB được gọi là đường xiên kẻ từ điểm A đến đường thẳng d.
- Đoạn thẳng HB được gọi là hình chiếu của đoạn thẳng AB lên đường thẳng d.
Định lý 1:
Trong các đường xiên và đường vuông góc kẻ từ một điểm bên ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2:
Trong hai đường xiên kẻ từ một điểm bên ngoài một đường thẳng đến đường thẳng đó:
- Đường xiên có hình chiếu lớn hơn là đường lớn hơn.
- Đường xiên lớn hơn có hình chiếu lớn hơn.
Nếu hai đường xiên bằng nhau thì hai hình chiếu cũng bằng nhau, và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên cũng bằng nhau.
